В чем измеряется угол наклона: Угол — Википедия – расчёт и таблица соотношений проценты-градусы.

определение угла, измерение углов, обозначения и примеры

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Определение угла

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.

Иначе говоря, луч или

полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол

– это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Точка на прямой

Как определить угол наклона крыши в градусах

Как рассчитать угол наклона крыши

Как рассчитать угол наклона крыши

Проекты возводимых загородных особняков могут учитывать множество требований, пожеланий и даже причуд или «капризов» их владельцев владельца. Но всегда их «роднит» общая особенность — без надежной крыши никогда не обходится ни одно их зданий. И в этом вопросе на первый план должны выходить не столько архитектурные изыски заказчика, сколько специфические требования к этому элементу строения. Это надежность и устойчивость всей стропильной системы и кровельного покрытия, полноценное выполнение крышей своего прямого предназначения – защиты от проникновения влаги (а в ряде случаев, кроме того, еще и термо- и звукоизоляции), при необходимости – функциональность расположенных непосредственно под кровлей помещений.

Проектирование конструкции крыши – дело чрезвычайно ответственное и достаточно непростое, особенно при сложных ее конфигурациях. Разумнее всего будет доверить это дело профессионалам, которое владеют методикой проведения необходимых расчетов и соответствующим программным обеспечение для этого. Однако, владельцу дома тоже могут быть интересны некоторые теоретические моменты. Например, немаловажно знать, как рассчитать угол наклона крыши самостоятельно, хотя бы приблизительно — для начала. Это даст возможность сразу прикинуть возможность реализации своих «авторских прикидок» — по соответствию задуманного реальным условиям региона, по «архитектуре» самой крыши, по планируемому кровельному материалу, по использованию чердачного помещения. В определенной степени рассчитанный угол ската кровли поможет провести предварительный подсчет параметров и количества пиломатериалов для стропильной системы, общей площади кровельного покрытия.

В каких величинах удобнее измерять угол ската крыши?

Казалось бы – совершенно излишний вопрос, так как все со школьной скамьи знают, что угол измеряется в градусах. Но ясность здесь все же нужна, потому что и в технической литературе, и в справочных таблицах, и в привычном обиходе некоторых опытных мастеров нередко встречаются и иные единицы измерения – проценты или же относительные соотношения сторон.

И еще одно необходимое уточнение — что принимается за угол наклона крыши?

Угол наклона – это угол, образованный пересечением двух плоскостей: горизонтальной и плоскостью ската кровли. На рисунке он показан буквой греческого алфавита α.

Интересующие нас острые углы (тупоугольных скатов не может быть просто по определению), лежит в диапазоне от 0 до 90°. Скаты круче 50 ÷ 60 ° в «чистом» виде встречаются чрезвычайно редко и то, как правило, для декоративного оформления крыш – при строительстве остроконечных башенок в готическом стиле. Однако есть и исключение – такими крутыми могут быть скаты нижнего ряда стропил крыши мансардного типа.

И все же чаще всего приходится иметь дело со скатами, лежащим в диапазоне от 0 до 45°

С градусами понятно – все, наверное, представляют транспортир с его делениями. А ка быть с другими единицами измерения?

Тоже ничего сложного.

Относительное соотношение сторон – это максимально упрощенная дробь, показывающая отношение высоты подъёма ската (на рисунке выше обозначена латинской Н) к проекции ската крыши на горизонтальную плоскость (на схеме – L).

L – это может быть, в зависимости от конструкции крыши, половина пролета (при симметричной двускатной крыше), пролет полностью (если крыша односкатная), либо, при сложных конфигурациях кровли, действительно линейный участок, определяемый проведенной к горизонтальной плоскости проекцией. Например, на схеме мансардной крыши такой участок хорошо показан – по горизонтальной балке от самого угла до вертикальной стойки, проходящей от верхней точки нижнего стропила.

Угол уклона так и записывается, дробью, например «1. 3».

Однако, на практике нередко случается так, что использовать величину угла уклона в таком представлении будет чрезвычайно неудобен, если, скажем, числа в дроби получаются некруглые и несокращаемые. Например, мало что скажет неопытному строителю соотношение 3. 11. На этот случай есть возможность воспользоваться еще одной величиной измерения уклона крыши – процентами.

Находится эта величина чрезвычайно просто – необходимо просто найти результат деления уже упомянутой дроби, а затем умножить его на 100. Например, в приведенном выше примере 3. 11

3. 11 = 0,2727 × 100 = 27,27 %

Итак, получена величина уклона ската кровли, выраженная в процентах.

А что делать, если требуется перейти от градусов к процентам или наоборот?

Можно запомнить такое соотношение. 100 % — это угол 45 градусов, когда катеты прямоугольного треугольника равны между собой, то есть в нашем случае высота ската равна длине его горизонтальной проекции.

В таком случае, 45° / 100 = 0,45° = 27´. Один процент уклона равен 27 угловым минутам.

Если подойти с другой стороны, то 100 / 45° = 2,22 %. То есть получаем, что один градус – это 2, 22% уклона.

Для простоты перевода величин из одних в другие можно воспользоваться таблицей:

Для наглядности будет полезным привести графическую схему, которая очень доступно показывает взаимосвязь всех упомянутых линейных параметров с углом ската и величинами его измерения.

К этому рисунку еще предстоит вернуться, когда будут рассматриваться виды кровельных покрытий.

Зависимость типа кровельного покрытия от крутизны ската

Планируя постройку собственного дома, хозяин участка наверняка уже проводит «прикидку» и своей голове, и с членами семьи – как будет выглядеть их будущее жилье. Кровля в этом вопросе, безусловно, занимает одно из первостепенных значений. И вот здесь необходимо учитывать то, что далеко не всякий кровельный материал может использоваться на различных по крутизне скатах крыш. Чтобы не возникало недоразумений позднее, необходим заранее предусматривать эту взаимосвязь.

Крыши по углу наклона ската можно условно разделит на плоские (уклон до 5°), с малым уклоном (от 6 до 30°) и крутоуклонные, соответственно, с углом ската более 30°.

У каждого из типов крыш есть свои достоинства и недостатки. Например, плоские крыши имеют минимальную площадь, но потребуют особых мер гидроизоляции. На крутых крышах не задерживаются снежные массы, однако они больше подвержены ветровой нагрузке из-за своей «парусности». Так и кровельный материал – в силу собственных технологических или эксплуатационных особенностей имеет определенные ограничения на применения с разными уклонами скатов.

Обратимся к уже рассматриваемому ранее рисунку (схема A). Черными кружками с дугообразными стрелками и синими цифрами обозначены области применения различных кровельных покрытий (острие стрелки указывает на минимально допустимое значение крутизны ската):

1 – это дранка, щепа, натуральный гонт. В этой же области лежит и применение до сих пор используемых в южных краях камышовых кровель.

2 – натуральное штучное черепичное покрытие, битумно-полимерные плитки, сланцевые плитки.

3 – рулонные материалы на битумной основе, не менее четырёх слоев, с внешней гравийной посыпкой, утопленной в слой расплавленной мастики.

4 – аналогично пункту 3, но для надёжности кровли достаточно трех слоев рулонного материала.

5 – аналогичные вышеописанным рулонные материалы (не менее трех слоев), но без наружной защитной гравийной посыпки.

6 – рулонные кровельные материалы, наклеиваемые на горячую мастику не менее, чем в два слоя. Металлочерепица, профнастил.

7 – волнистые асбестоцементные листы (шифер) унифицированного профиля.

8 – черепичное глиняное покрытие.

9 – асбестоцементные листы усиленного профиля.

10 – кровельная листовая сталь с развальцовкой соединений.

11 – шиферное покрытие обычного профиля.

Таким образом, если есть желание покрыть крышу кровельным материалом определенного типа, угол уклона ската должен планироваться в указанных рамках.

Зависимость высоты конька от угла наклона крыши

Для тех читателей, которые хорошо помнят курс тригонометрии средней школы, этот раздел может показаться неинтересным. Они могут сразу его пропустить и перейти дальше. А вот подзабывшим это нужно освежить знания о взаимозависимости углов и сторон в прямоугольном треугольнике.

Для чего это надо? В рассматриваемом случае возведения крыши всегда в расчетах отталкиваются от прямоугольного треугольника. Два его катета – это длина проекции ската на горизонтальную плоскость (длина пролета, половины пролета и т.п. – в зависимости от типа крыши) и высота ската в высшей точке (на коньке или при переходе на верхние стропила – при расчете нижних стропил мансардной крыши). Понятно, что постоянная величина здесь одна – это длина пролета. А вот высоту можно изменять, варьируя угол наклона крыши.

В таблице приведены две основные зависимости, выраженные через тангенс и синус угла наклона ската. Существуют и иные зависимости (через косинус или котангенс) но в данном случае нам достаточно этих двух тригонометрических функций.

Зная эти тригонометрические тождества, можно решить практически все задачи по предварительному проектированию стропильной конструкции.

Так, если необходимо «плясать» от четко установленной высоты подъёма конька, то отношением tg α = H / L несложно будет определить угол.

По полученному делением числу в таблице тангенсов находят угол в градусах. Тригонометрические функции часто бывают заложены в инженерные калькуляторы, они есть в обязательном порядке в таблицах Exel (для тех, кто умеет работать с этим удобным приложением. Правда, там расчет ведется не в градусах, а в радианах). Но чтобы нашему читателю не приходилось отвлекаться на поиски нужных таблиц, приведем значение тангенсов в диапазоне от 1 до 80°.

В случае, наоборот, когда за основу берется угол наклона кровли, высота расположения конька определяется по обратной формуле:

H = L × tg α

Теперь, имея значения двух катетов и угла наклона кровли, очень просто вычислить и требуемую длину стропила от конька до карнизного свеса. Можно применить теорему Пифагора

S = √ (L² + H²)

Или же, что, наверное, проще, так как уже известна величина угла, применить тригонометрическую зависимость:

Уклон скатов крыши — от чего зависит и в чём он измеряется.

Такой немаловажный для крыши факт — её уклон. Уклон крыши — это угол наклона кровли относительно горизонтального уровня. По углу наклона скатов крыши бывают малоуклонные (пологие), средней наклонности и крыши с крутыми (сильноуклонными) скатами .

Малоуклонная крыша та крыша. монтаж которой осуществляется из расчёта наименьшего, рекомендованного угла наклона скатов. Так для каждого кровельного покрытия есть свой рекомендуемый минимальный уклон.

От чего зависит уклон кровли

• От способности крыши защищать строение от внешних факторов и воздействий.
• От ветра — чем больше уклон крыши, тем больше значение приходящихся ветровых нагрузок. При крутых уклонах уменьшается сопротивляемость ветру, повышается парусность. В регионах и местах с сильными ветрами рекомендуется применять минимальный уклон крыши, чтоб уменьшить нагрузки на несущие конструкции крыши.
• От кровельного покрытия (материала) — Для каждого кровельного материала существует свой минимальный угол наклона, при котором можно использовать данный материал.
• От архитектурных задумок, решений, местных традиций — так в разных регионах отдаётся предпочтение для той или иной конструкции крыши.
• От атмосферных осадков. снеговых нагрузок и дождей в регионе. На крышах с большим уклоном не будет скапливаться в огромных количествах снег, грязь и листья.

В чем измеряется угол уклона крыши

Обозначение уклона кровли на чертежах может быть как в градусах, так и в процентах. Уклон крыши обозначается латинской буквой i .

В СНиПе II-26-76, данная величина указывается в процентах ( % ). В данный момент не существует строгих правил по обозначению размера уклона крыши.

Единицей измерения уклона крыши считают градусы или проценты ( %). Их соотношение указаны ниже в таблице.

Уклон крыши соотношение градусы-проценты

Замер уклона крыши

Измеряют угол уклона при помощи уклономера или же математическим способом.

Уклономер — это рейка с рамкой, между планками которой есть ось, шкала деления и к которой закреплён маятник. Когда рейка находится в горизонтальном положении, на шкале показывает ноль градусов. Чтобы произвести замер уклона ската крыши, рейку уклономера держат перпендикулярно коньку, то есть в вертикальном уровне. По шкале уклономера маятник указывает, какой уклон у данного ската крыши в градусах. Такой метод замера уклона стал уже менее актуален, так как сейчас появились разные геодезические приборы для замеров уклонов, а так же капельные и электронные уровни с уклономерами.

Математический расчёт уклона

Можно рассчитать уклон крыши не используя геодезические и другие приборы для замеров уклона. Для этого необходимо знать два размера:

• Вертикальная высота ( H ) от верхней точки ската (как правило конька) до уровня нижней (карниза)
• Заложение ( L ) — горизонтальное расстояние от нижней точки ската до верхней

При помощи математического расчёта величину уклона крыши находит следующим образом:

Угол уклона ската i равен отношению высоты кровли Н к заложению L

Для того, чтобы значение уклона выразить в процентах, это отношение умножают на 100. Далее,чтобы узнать значение уклона в градусах, переводим по таблице соотношений, расположенной выше.

Чтобы было понятней рассмотрим на примере:

Длина заложения 4,5 м, высота крыши 2,0 м.

Уклон равен: i = 2.0. 4,5 = 0,44 теперь умножим на × 100 = 44 %. Переводим данное значение по таблице в градусы и получаем — 24 0.

Минимальный уклон для кровельных материалов (покрытий)

Определение номинального угла наклона кровли

Сложно представить себе любое здание без крыши. Кровля должна защищать здание от воздействия природных осадков, обладать огнестойкими и водонепроницаемыми свойствами, обеспечивать эффективный отвод атмосферных осадков. Долговечность эксплуатации здания и его отдельных элементов во многом зависит от качественной крыши. Для достижения лучших результатов стоит использовать более простые виды скатных крыш: односкатные, двухскатные, вальмовые, полувальмовые, мансардные.

Минимальный угол наклона крыши из металлочерепицы должен составлять 14 градусов.

Основные данные

График выбора кровельного материала в зависимости от уклона крыши.

Допустимый угол наклона металлической крыши обычно измеряют своими руками исходя из климатических условий того района, в котором ведется строительство, и кровельного материала. Минимально угол наклона должен составлять 110°, максимальный угол наклона можно определить путем анализа погодных условий, его значение может быть 45°. и больше. Для более теплого и сухого климата используется менее пологая крыша. Более крутой угол наклона дает возможность минимально скапливать снег и, соответственно, снижать снеговую нагрузку. Например, уклон 45° позволяет почти не учитывать вес снежного покрова.

Наряду с этим, увеличенный угол наклона резко повышает давление ветра на крышу. При уклоне в 45° давление ветра больше в 5 раз по сравнению с показателем в 11°. Следовательно, для большего угла наклона возникает необходимость в большем количестве реек для усиления обрешетки и стропил. От угла уклона крыши прямо зависит и ее стоимость.

Для кровли с углом наклона около 40-45° необходимо больше материалов (примерно в 1,5 раза), нежели для плоской крыши, а для 60° требуется в 2 раза больше кровельных материалов. При выборе конфигурации важно помнить, что от угла наклона напрямую зависит выбор кровельных материалов. Учет угла наклона позволяет определить материалы для кровли, а также произвести расчет слоев крыши и ее площади.

Зависимость полезной площади мансарды от уклона крыши.

Материалы для кровли по своим свойствам (технические, экономические, физические) объединились в группе 1-11.

На графике они показаны дугообразными стрелками. Линии наклона показывают уклон ската. Выделенная (жирным) линия на графике обозначает отношение полной высоты данного конька h к половине его обычного заложения ½. Отношение 1/2 указывает, что вертикальный отрезок h располагается на горизонтальном отрезке ½ два раза. Наклонная линия на полукруглой шкале обозначает угол наклона в градусах, а шкала, расположенная вертикально, — уклон крыши в %.

Так рассчитывают минимальный уклон для тех или иных кровельных материалов. В качестве примера, с помощью данного графика проведем расчет нужного угла наклона для данной крыши с использованием металлической черепицы.

Как измерить уклон

Таблица соотношения градус/процент уклона кровли.

На графике ищем наклонную линию, с которой стыкуется дугообразная стрела 2. Пересечение наклонной линии c вертикальной шкалой определяет уклон, минимально допустимый для данной крыши, который равен 50%. Нам известно, что уклон ската определяется отношением высоты конька к половине его заложения. Произведем расчет таким образом:

i = 10 метров (заложение)

h = 4 метра (высота конька)

i= h / (1/2) = 4 / (10/2) = 0,8

Для того чтобы измерить уклон в %, это отношение умножают на 100

Таким образом, уклон в 80% при соблюдении норм строительства обеспечит достаточный сброс дождевой воды со всей площади. Для кровли из рулонных полимерно-битумных, битумных и мастичных материалов с уклоном 10° необходим защитный слой для основного водоизоляционного покрова из гравия либо каменной крошки, у которой марка морозостойкости не меньше 100. Такой же защитный слой применяется для кровли крыши с помощью пленочных рулонных материалов с углом до 2,5%. Слой для защиты из гравия должен быть толщиной 1-1,6 см, а слой крупнозернистой посыпки — 0,3-0,5 см.

Причем на крышах с уклоном примерно до 2,5% с использованием эластомерных пленочных материалов в рулонах, выполненных свободной кладкой, необходим утяжеляющий слой гравия из расчета 50 кгс/кв.м.

На крышах из битумно-полимерных или битумных покрытий в рулонах с углом наклона выше 10% верхний слой гидроизоляционного покрова выполняется из крупнозернистой посыпки. На крышах из мастичных материалов с углом больше 10% предусматривается защитный слой из красочных составов.

При создании крыши из асбестоцементных листов, а также профнастила и металлической черепицы с наклоном до 20% по всей площади необходимо производить герметизацию стыков. Не более чем на 5% можно допустить отклонение уклона кровли из мелкоштучных материалов. Производя эти расчеты, можно узнать площадь помещения мансарды или чердака.

Единицы измерения и инструменты

В основание металлической конструкции встроены цифровой дисплей с элементами управления.

Величина уклона на всех чертежах может обозначаться в градусах или в процентах, а сам он обозначается буквой «i». В настоящий момент нет строгих правил, как обозначать данную величину. Единицей измерения считают градусы или проценты (%).

Угол уклона измеряется двумя способами:

1. Специальным уклономером.
2. Математическим способом, с помощью вычислений.

Уклономер — это специальная рейка с рамкой, у которой между планками есть ось, на которой закреплен маятник, и своя шкала деления. Когда эта рейка расположена в горизонтальном положении, то маятник на ее шкале отклонен на ноль градусов. Для произведения измерения уклона ската рейку прибора располагают перпендикулярно коньку, в вертикальном положении.

По шкале определяют угол отклонения маятника, который указывает уклон этого ската данной крыши в градусах. Этот метод определения применяется очень и очень редко. На данный момент разработано множество геодезических приборов для определения этих величин и специальные уровни-уклономеры, как капельные, так и электронные.

Можно спокойно рассчитать наклон данной крыши, не прибегая к использованию специальных геодезических, механических и других видов приборов для замеров уклона. Необходимо просто измерить некоторые параметры крыши:

1. Вертикальная высота (обозначается как H) — высота от верхней точки данного ската (обычно считают от конька) до самой нижней точки (так называемого карниза).
2. Заложение — горизонтальный промежуток от самой нижней точки данного ската до самой верхней его точки.

Уклон крыши (его величину) с применением математического расчета находят так.

Угол наклона отдельного ската i выражается через отношение измеренной высоты крыши Н к расстоянию заложения L. Таким образом

Для точного определения этого значения в процентах отношение i умножают на 100. Затем, для определения его значения в градусах, мы производим перевод процентов в градусы.

Для полного понимания этого метода приведем наглядный расчет:

высота равна 3,0 м,

длина заложения равна 5 м.

По формуле вычисляем i:

Источники: http://www.spbud.com.ua/articles/kak-rasschitat-ugol-naklona-krishi-58.html, http://krovli.club/uklon-kryshi, http://1metallocherepica.ru/raschet/kak-opredelit-uklon-krovli.html

Как определить угол наклона крыши в градусах

Как сделать расчет уклона крыши – важные особенности

Чтобы крыша здания могла в полной мере выполнять все возложенные на нее функции, необходимо при ее создании учесть ряд параметров. Одним из самых важных параметров крыши является ее уклон, который обеспечивает отвод атмосферных осадков с ее поверхности и влияет на способность выдерживать внешние нагрузки. О том, как посчитать наклон крыши, и пойдет речь в данной статье.

Определение наклона крыши — от чего зависит

Чтобы провести правильный расчет уклона крыши, необходимо учитывать несколько факторов, среди которых сильнее всего выделяются следующие:

1. Ветровые нагрузки. На уклон скатов очень сильно влияет ветер. Чтобы крыша могла нормально сопротивляться его воздействию, нужно правильно подобрать ее угол. При слишком больших углах нагрузка на них будет высокой, но чрезмерное уменьшение угла тоже может быть опасным – пологую кровлю сильным порывом ветра может попросту сорвать.
2. Снеговые и дождевые нагрузки. Со снегом все довольно просто – повышение угла наклона упрощает его схождение с поверхности кровли. При наклоне крыши более 45 градусов снег почти не будет задерживаться на ней. При малом угле наклона кровли может появляться снеговой мешок, который увеличивает нагрузку на крышу. С дождевыми осадками такая же ситуация – если угол наклона кровли будет слишком низким, то вода сможет затекать в стыки или вообще застаиваться на поверхности крыши.

Отталкиваясь от этих факторов, можно рассчитывать угол наклона скатов. Кроме того, перед тем, как рассчитать угол двухскатной крыши, стоит обратить внимание на рекомендуемые показатели: для местности с сильными ветрами подойдет уклон в 15-20 градусов, а в остальных случаях оптимальная величина уклона составляет 35-40 градусов. Разумеется, нужно понимать, что расчет двухскатной крыши индивидуален, и выбирать усредненные показатели просто так нежелательно.

Методика проведения расчетов

При проектировании крыши нужно в обязательном порядке проводить ряд расчетов, среди которых всегда должен присутствовать расчет угла наклона скатов. Данный параметр напрямую влияет на конструкцию крыши: при увеличении наклона снижается снеговая нагрузка, но увеличивается воздействие ветра, поэтому стропильную систему приходится дополнительно усиливать. Для обустройства скатов под большим углом требуется еще и большее количество материалов, что негативно сказывается на стоимости строительства.

Перед тем, как узнать градус наклона крыши, нужно рассчитать эксплуатационную нагрузку на крышу, для чего требуется два параметра:

• Общую массу кровельной конструкции;
• Пиковые уровни снежных осадков, свойственные региону, где проходит строительство.

Упрощенный алгоритм расчетов сводится к следующим действиям:

• Сначала нужно определить вес одного квадратного метра кровельного пирога;
• Полученное значение умножается на общую площадь кровли;
• Масса кровли умножается на коэффициент 1,1.

Пример расчета уклона кровли в градусах

Чтобы понять, как высчитать угол крыши, стоит рассмотреть процесс расчетов на конкретном примере. Для примера будут взяты следующие данные: обрешетка имеет толщину 2,5 см, один квадратный метр кровли весит 15 кг, в качестве теплоизоляционного материала используется утеплитель толщиной 10 см, квадратный метр которого имеет вес 10 кг, а для покрытия используется ондулин с весом 3 кг на квадратный метр.

Расчет ската крыши проводится в соответствии с описанной выше методикой. Подстановка имеющихся данных приводит к следующему выражению: (15+10+3)х1,1 = 30,8 кг/кв.м. Полученная величина вполне допустима – среднестатистическая нагрузка на крышу жилых зданий составляет немногим меньше 50 кг/кв.м. Кроме того, в формуле присутствует коэффициент 1,1, который немного увеличивает фактический вес кровельной конструкции и позволяет в дальнейшем заменить кровельное покрытие на более тяжелое.

Как узнать угол наклона крыши

Между уклоном кровельных скатов и снежной нагрузкой имеется прямая зависимость. Если угол наклона крыши меньше 25 градусов, то коэффициент снежной нагрузки равен 1, а при углах, варьирующихся в пределах от 25 до 60 градусов, то этот коэффициент увеличивается до 1,25. Крыша с большим углом наклона не будет подвергаться снежным нагрузкам вообще, поэтому они не учитываются при расчетах.

Чтобы определить угол наклона крыши, нужно воспользоваться таблицей Брадиса и простой методикой: высота кровельной конструкции делится на длину фронтона, разделенную на два, после чего остается найти таблице угол, который соответствует полученному результату.

Высота крыши в коньке определяется следующим образом:

• Первым делом нужно рассчитать ширину пролета;
• Полученная величина делится на 2;
• Чтобы сделать расчет высоты конька, результат предыдущего расчета умножается на коэффициент, соответствующий определенному углу наклона.

На примере реализация такой методики расчета выглядит так: при ширине здания, равной 8 метрам, и 25-градусном уклоне кровли, расчетный коэффициент составляет 0,47. В итоге подстановки значений получается выражение следующего вида: 4х0,47 = 1,88 м. Полученная величина – это высота крыши, соответствующая имеющимся исходным данным.

Выбор кровельного покрытия в зависимости от наклона крыши

На рынке материалы для крыши присутствуют в большом ассортименте, поэтому с выбором подходящего варианта особых проблем не будет. Кровельные покрытия отличаются по характеристикам и возможностям применения, и все их параметры необходимо изучить перед тем, как измерить угол крыши – только в этом случае удастся создать надежную и эффективную конструкцию.

Выбирая материал для кровли, стоит отталкиваться от следующих рекомендаций:

1. Если угол наклона стропил составляет от 2,5 до 10 градусов, то лучше всего подойдут покрытия из каменной крошки или гравия. В первом случае верхний слой покрытия имеет толщину 3-5 мм, а во втором – 10-15 мм.
2. При наклоне более 10 градусов оптимальным вариантом будут крупнозернистые или рулонные материалы, дополненные битумной гидроизоляцией.
3. Для обустройства скатных крыш с углом наклона не более 20 градусов обычно используется профнастил или листовой асбестоцемент. Все швы и стыки между кровельными материалами должны быть обработаны герметиком.
4. Если угол наклона крыши находится в пределах 20-60 градусов, то она чаще всего накрывается металлическими листами. Стыки материалов в данном случае нужно в обязательном порядке герметизировать.

Заключение

Знание того, как узнать угол наклона крыши в градусах, существенно упростит процесс ее проектирования и позволит создать максимально надежную конструкцию, которая сможет хорошо защищать коробку здания от атмосферных осадков, ветра и холода.

Уклон крыши

Уклон скатов крыши — от чего зависит и в чём он измеряется.

Такой немаловажный для крыши факт — её уклон. Уклон крыши — это угол наклона кровли относительно горизонтального уровня. По углу наклона скатов крыши бывают малоуклонные (пологие), средней наклонности и крыши с крутыми (сильноуклонными) скатами.

Малоуклонная крыша та крыша, монтаж которой осуществляется из расчёта наименьшего, рекомендованного угла наклона скатов. Так для каждого кровельного покрытия есть свой рекомендуемый минимальный уклон.

От чего зависит уклон кровли

• От способности крыши защищать строение от внешних факторов и воздействий.
• От ветра — чем больше уклон крыши, тем больше значение приходящихся ветровых нагрузок. При крутых уклонах уменьшается сопротивляемость ветру, повышается парусность. В регионах и местах с сильными ветрами рекомендуется применять минимальный уклон крыши, чтоб уменьшить нагрузки на несущие конструкции крыши.
• Откровельного покрытия (материала) — Для каждого кровельного материала существует свой минимальный угол наклона, при котором можно использовать данный материал.
• От архитектурных задумок, решений, местных традиций — так в разных регионах отдаётся предпочтение для той или иной конструкции крыши.
• От атмосферных осадков: снеговых нагрузок и дождей в регионе. На крышах с большим уклоном не будет скапливаться в огромных количествах снег, грязь и листья.

В чем измеряется угол уклона крыши

Обозначение уклона кровли на чертежах может быть как в градусах, так и в процентах. Уклон крыши обозначается латинской буквой i .

В СНиПе II-26-76, данная величина указывается в процентах ( % ). В данный момент не существует строгих правил по обозначению размера уклона крыши.

Единицей измерения уклона крыши считают градусы или проценты ( %). Их соотношение указаны ниже в таблице.

Уклон крыши соотношение градусы-проценты

градусы	%	градусы	%	градусы	%
1°	1,75%	16°	28,68%	31°	60,09%
2°	3,50%	17°	30,58%	32°	62,48%
3°	5,24%	18°	32,50%	33°	64,93%
4°	7,00%	19°	34,43%	34°	67,45%
5°	8,75%	20°	36,39%	35°	70,01%
6°	10,51%	21°	38,38%	36°	72,65%
7°	12,28%	22°	40,40%	37°	75,35%
8°	14,05%	23°	42,45%	38°	78,13%
9°	15,84%	24°	44,52%	39°	80,98%
10°	17,64%	25°	46,64%	40°	83,90%
11°	19,44%	26°	48,78%	41°	86,92%
12°	21,25%	27°	50,95%	42°	90,04%
13°	23,09%	28°	53,18%	43°	93,25%
14°	24,94%	29°	55,42%	44°	96,58%
15°	26,80%	30°	57,73%	45°	100%

Перевести уклон из процентов в градусы и наоборот из градусов в проценты можно при помощи онлайн конвертера:

Конвертер уклона — онлайн калькулятор

из градусов в проценты и из процентов в грудусы Перейти

Замер уклона крыши

Измеряют угол уклона при помощи уклономера или же математическим способом.

Уклономер — это рейка с рамкой, между планками которой есть ось, шкала деления и к которой закреплён маятник. Когда рейка находится в горизонтальном положении, на шкале показывает ноль градусов. Чтобы произвести замер уклона ската крыши, рейку уклономера держат перпендикулярно коньку, то есть в вертикальном уровне. По шкале уклономера маятник указывает, какой уклон у данного ската крыши в градусах. Такой метод замера уклона стал уже менее актуален, так как сейчас появились разные геодезические приборы для замеров уклонов, а так же капельные и электронные уровни с уклономерами.

Математический расчёт уклона

Можно рассчитать уклон крыши не используя геодезические и другие приборы для замеров уклона. Для этого необходимо знать два размера:

• Вертикальная высота ( H ) от верхней точки ската (как правило конька) до уровня нижней (карниза)
• Заложение ( L ) — горизонтальное расстояние от нижней точки ската до верхней

При помощи математического расчёта величину уклона крыши находит следующим образом:

Угол уклона ската i равен отношению высоты кровли Н к заложению L

Для того, чтобы значение уклона выразить в процентах, это отношение умножают на 100. Далее,чтобы узнать значение уклона в градусах, переводим по таблице соотношений, расположенной выше.

Чтобы было понятней рассмотрим на примере:

Длина заложения 4,5 м, высота крыши 2,0 м.

Уклон равен: i = 2.0 : 4,5 = 0,44 теперь умножим на × 100 = 44 %. Переводим данное значение по таблице в градусы и получаем — 24°.

Таблица уклонов кровли

Строительство крыши –важный заключительный этап строительства дома. Крыша защищает дом от агрессивного воздействия окружающей среды, придает постройке эстетичный вид.

Плоски крыши преобладают в многоэтажных домах, в частных домах и коттеджах – скатные. Угол наклона крыши – важный расчетный показатель.

Виды крыш и их зависимость от угла наклона

Существует несколько видов крыш, в зависимости от устройства кровли:

• Односкатная крыша – наклонная плоскость, лежащая на стенах разной высоты.
• Двухскатная крыша – состоит из двух скатов, является надежной и простой.
• Вальмовая крыша – состоит из 4-х скатов со срезанными вершинами.
• Шатровое перекрытие – несколько равнобедренных треугольников, соединенных между собой вершинами.

Если угол наклона кровли более 10°, то крыша считается скатной.

От чего зависит уклон кровли

• от ветра
• от кровельного покрытия
• от архитектурных задумок
• от атмосферных осадков (снега и дождя)

Уклон крыши – это угол наклона кровли относительно горизонта.

Показатель уклона позволяет:

1. Подобрать кровельный материал
2. Правильно рассчитать количество снегодержателей

Зная одну из величин по таблице можно найти остальные значения.

Минимальный уклон для кровельных материалов (покрытий)

Вид кровли	Минимальный уклон крыши		в соотношении высоты ската к заложению
	в градусах	в %
Кровли из рулонных битумных материалов: 3-х и 4-х слойные (наплавляемая кровля)	0-3 0	до 5%	до 1:20
Кровли из рулонных битумных материалов: 2-х слойные (наплавляемая кровля)	от	15
Фальцевая кровля	от 4 0
Ондулин	5 0	1:11
Волнистые асбоцементные листы (шифер)	9 0	16	1:6
Керамическая черепица	11 0	1:6
Битумная черепица	11 0	1:5
Металлочерепица	14 0
Цементно-песчанная черепица	34 0	67%	1:1,5
Деревянная кровля	39 0	80%	1:1.125

Пример №1.

H = 2 м
I = 2,86 м

Рассчитаем угол кровли (i): 2/2,86 = 0,699. Это 35° по данным таблицы.

Пример №2

Коэффициент уклона кровли 1,006. Найти: градус уклона кровли.

По таблице этому коэффициенту соответствует значение в 6° градусов.

Расчет угла наклона крыши

Крыша – это один из важнейших элементов любого строения. Именно она надежно защищает здание от воздействия негативных факторов окружающей среды, от атмосферных осадков.

Разумеется, хорошая конструкция должна быть водонепроницаемой, обеспечивать качественный отвод атмосферных вод, а также обладать высокой устойчивостью к огню. Вместе с тем, крыша должна быть удобной для проведения ремонта в период ее эксплуатации.

Следует помнить, что именно от надежности и качества кровли вашего дома будет напрямую зависеть, сколько прослужит само здание. В настоящее время многие домовладельцы отдают предпочтение покатой крыше.

Надо сказать, у такой конструкции есть несколько очевидных преимуществ. Кроме того, следует правильно делать расчет угла наклона крыши.

Плюсы покатой крыши

Простые конструкции, такие, как односкатные и двускатные крыши, вальмовые или мансардные, всегда были и остаются самыми качественными и надежными вариантами. Без сомнения, преимущество покатой крыши заключается именно в гармоничном сочетании отличного качества и простоты в исполнении.

Такая крыша состоит из базового элемента кровли, а также обрешетки и стропил.

Что касается кровли, она служит для защиты здания от воздействия природных явлений, снега и дождя. Стропила же, а также обрешетки, поддерживают всю конструкцию, передают нагрузку на стены.

Рис. 1 Рассчитываем угол наклона крыши

Следует заметить, что покатая крыша защищает здание от осадков за счет определенного наклона кровли.

Прежде, чем приступить к монтажу покатой (или, как ее еще называют, скатной) крыши, необходимо произвести точный расчет угла наклона крыши.

Даже для тех людей, которые не являются специалистами в области строительства крыш, совершенно очевидно: чем угол наклона меньше, тем больше возникнет впоследствии проблем с герметичностью.

И это абсолютно не зависит от того, какой строительный материал вы выбираете для покрытия вашей крыши.

Факторы, которые влияют на выбор угла наклона

Конечно же, вам следует знать при расчете угла уклона крыши, какие факторы необходимо принимать во внимание. Так, среди важнейших параметров можно назвать:

• Ветер. Само собой разумеется, что крыша будет оказывать большее сопротивление ветру при большем наклоне. Однако слишком большой угол наклона является достаточно опасным для крыши. Так, например, при увеличении угла с минимального показателя (11 градусов) до 45 градусов, ветровая нагрузка возрастает в пять раз. Но с другой стороны, при выборе очень маленького угла наклона возникает другая проблема: при сильном порыве ветра кровлю может просто сорвать;
• Снег и дождь. Совершенно очевидно, что снег лучше сходит с крыши, имеющей большой угол наклона. Так, если он составляет более 45 градусов, обеспечено полное скатывание снега. И чем выше угол наклона, тем более герметичной будет красивая кровля вашей крыши. Объяснить это легко: дело в том, что при воздействии на крышу ветер обычно загоняет под стыки кровли атмосферную воду. Но чем больше вы сделаете уклон крыши, тем меньше вероятность попадания воды под стыки кровельных материалов.

Исходя из этих факторов, необходимо производить расчет угла наклона крыши. Для районов с сильными показателями ветра специалисты рекомендуют наклон крыши в 15-20 градусов, а для районов с нормальными показателями – около 35-40 градусов.

Однако следует помнить, что расчет угла наклона крыши обязательно нужно производить индивидуально для каждого конкретного здания.

Следует также подчеркнуть, что при расчете обязательно следует учесть особенности не только климата местности, но и конструкции самого строения.

Рис. 2 Формы скатных крыш

Способы произведения расчетов

Следует помнить, что подбор правильного угла – это очень важный этап конструирования будущей крыши здания. Обычно угол наклона крыши составляет от 11 и до 45 градусов, конечно же, бывают и исключения.

В том случае, если увеличить угол наклона, уменьшается, соответственно, снеговая нагрузка на крышу.

Но вместе с тем, чем больше будет показатель, тем воздействие ветра окажется сильнее. Это приводит к тому, что при возведении крыши требуются более прочные строительные материалы, стропила и обрешетки. А это значит, что будущая крыша обойдется вам дороже.
расчет уклона крыши

Помните: угол наклона влияет напрямую не только на качество, но и на количество материала для обустройства кровли.

Чем больше угол, тем, соответственно, больших денег будет стоить кровля.

Определенный угол уклона придается крыше в зависимости от выбранного материала, а также от климатических условий. В случае, если в районе в большом количестве наблюдаются атмосферные осадки, уклон крыши должен быть круче.

Соответствующий угол наклона будущей крыши можно определить, учитывая предполагаемую нагрузку. Как же рассчитать нагрузку? Для этого вам нужно принимать во внимание два показателя:

• Вес будущей конструкции;
• Нагрузку снега для данной местности.

Первым делом, нужно взять вес квадратного метра каждого слоя кровли, а затем сложить показатели для всех слоев. Следующий шаг: умножение получившегося результата на показатель 1,1.

Наглядный пример подобных расчетов

Предположим, толщина вашей обрешетки составляет 2,5 сантиметра, и 1 квадратный метр будет весить 15 килограммов. Вы планируете класть утеплитель толщиной 10 сантиметров: вес этого материала составляет около 10 килограммов на квадратный метр.

Также вам предстоит использовать Ондулин, весом 3 килограмма на квадратный метр.

Итак, наш расчет: 15+10+3 * 1,1 = 30,8 килограммов на квадратный метр. По усредненным показателям, для жилых домов нагрузка на кровлю обычно не превышает 50 килограммов на один квадратный метр.

Следует заметить, что для ряда покрытий сильно завышена допустимая нагрузка, однако, вам не нужно этим пренебрегать.

Предположим, вы решите лет через двадцать сменить кровлю, и кровельный ковер будет тяжелее, чем раньше. В данном случае и требуется тот самый коэффициент надежности 1,1 – его обязательно нужно учитывать, как коэффициент запаса.

Наконец, сделаем расчет нагрузки от собственной массы крыши. Назовем ее для простоты Н1. Она будет равна:

Н1 = 50кг/кв.м*1.1 = 55 кг/кв.м.

И непременно помните: когда вы начнете считать сечение стропильной ноги, прибавьте вес стропила к весу будущего кровельного ковра.

Учимся пользоваться таблицей Брадиса

Что касается снеговой нагрузки, коэффициент будет зависеть от того, какой угол наклона вы выбрали для вашей крыши. Итак, если наклон составляет менее 25 градусов, коэффициент составляет 1, а если от 25 до 60 градусов, то принимается во внимание коэффициент, составляющий 1,25.

А вот в том случае, если вы выбираете угол наклона более 60 градусов, учитывать нагрузку от снега не нужно.

Если вам необходимо найти угол наклона кровли, воспользуйтесь математической таблицей Брадиса (таблицей тангенсов).

Высоту в коньке следует разделить на ? длины фронтона, и по соответствующему значению в таблице найти угол наклона.

А вот для того чтобы математическим способом вычислить высоту конька, следует рассчитать ширину пролета дома, разделить этот показатель на два, а затем умножить на относительную величину, которая будет индивидуальной для определенного угла наклона.

Также для определения угла наклона и высоты конька можно воспользоваться угольником.
расчет наклона крыши.

Попробуем разобраться на конкретном примере. Ширина будущего здания составляет 8 метров. Делим это значение на два, получаем 4 метра.

Рис.3 Зависимость угла наклона крыши от материала для кровли

Нам нужно определить высоту поднятия стропил в случае, если уклон кровли составляет 25 градусов. Итак, находим в соответствующей таблице показатель, соответствующий данному углу наклона: он составляет 0,47.

Умножаем половину ширины нашего здания на данную относительную величину. Получаем следующий расчет: 4*0,47=1,88. Соответственно, при таком раскладе нам нужно будет поднять стропила на высоту, составляющую 1,88 метра.

Рис. 4 Схема кровельной системы

Выбор кровельного материала в зависимости от угла наклона

Следует подчеркнуть, что все материалы для обустройства кровли объединяются в отдельные группы: по их физическим свойствам, техническим характеристикам, а также ценовым параметрам.

Приведем некоторые рекомендации, которые помогут вам подобрать наиболее подходящий материал для обустройства крыши:

• В том случае, если наклон кровли совсем небольшой, и составляет где-то от 2,5 до 10 градусов, обычно применяются покрытия из каменной крошки (крупнозернистой), а также из гравия. Слой верхнего покрытия составляет для гравия – 10-15 миллиметров, для каменной крошки – 3-5 миллиметров.
• Если уклон кровли составляет от 10 градусов, и при этом была использована базовая битумная водоизоляция, необходимо выполнить верхний слой из крупнозернистого материала. В том случае, если показатель такой же, а материал выбран пленочный рулонный, то необходимо будет использовать специальный окрасочный слой для защиты.
• В том случае, если угол кровли составляет до 20 градусов, а само покрытие выполняется из металлического профнастила, или же асбестоцементных листов, следует непременно провести герметизацию всех стыков. Стоит ли выбирать металлочерепицу.

При углах до 60 градусов нужно обязательно проводить герметизацию стыков листов кровли из меди или стали. При этом стыки непременно должны быть двойными.

Учитывая все перечисленные параметры и делая правильные расчеты, можно сконструировать надежную крышу, которая прослужит ни один год или десяток лет.

Телесный угол — Википедия

Материал из Википедии — свободной энциклопедии

Телесный угол

Теле́сный у́гол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол). Частными случаями телесного угла являются трёхгранные и многогранные углы. Границей телесного угла является некоторая коническая поверхность. Обозначается телесный угол обычно буквой Ω.

Телесный угол измеряется отношением площади той части сферы с центром в вершине угла, которая вырезается этим телесным углом, к квадрату радиуса сферы:

Ω=SR2.{\displaystyle \Omega \,=\,{S \over R^{2}}.}

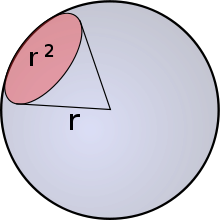
Телесные углы измеряются отвлечёнными (безразмерными) величинами. Единицей измерения телесного угла в системе СИ является стерадиан, равный телесному углу, вырезающему из сферы радиуса r поверхность с площадью r². Полная сфера образует телесный угол, равный 4π стерадиан (полный телесный угол), для вершины, расположенной внутри сферы, в частности, для центра сферы; таким же является телесный угол, под которым видна любая замкнутая поверхность из точки, полностью охватываемой этой поверхностью, но не принадлежащей ей. Кроме стерадианов, телесный угол может измеряться в квадратных градусах, квадратных минутах и квадратных секундах, а также в долях полного телесного угла.

Телесный угол имеет нулевую физическую размерность.

Двойственный телесный угол к данному телесному углу Ω определяется как угол, состоящий из лучей, образующих с любым лучом угла Ω неострый угол.

Коэффициенты пересчёта единиц телесного угла.

Ω{\displaystyle \Omega }	Стерадиан	Кв. градус	Кв. минута	Кв. секунда	Полный угол
1 стерадиан =	1	(180/π)² ≈ ≈ 3282,806 кв. градусов	(180×60/π)² ≈ ≈ 1,1818103⋅107 кв. минут	(180×60×60/π)² ≈ ≈ 4,254517⋅1010 кв. секунд	1/4π ≈ ≈ 0,07957747 полного угла
1 кв. градус =	(π/180)² ≈ ≈ 3,0461742⋅10−4 стерадиан	1	60² = = 3600 кв. минут	(60×60)² = = 12 960 000 кв. секунд	π/(2×180)² ≈ ≈ 2,424068⋅10−5 полного угла
1 кв. минута =	(π/(180×60))² ≈ ≈ 8,461595⋅10−8 стерадиан	1/60² ≈ ≈ 2,7777778⋅10−4 кв. градусов	1	60² = = 3600 кв. секунд	π/(2×180×60)² ≈ ≈ 6,73352335⋅10−9 полного угла
1 кв. секунда =	(π/(180×60×60))² ≈ ≈ 2,35044305⋅10−11 стерадиан	1/(60×60)² ≈ ≈ 7,71604938⋅10−8 кв. градусов	1/60² ≈ ≈ 2,7777778⋅10−4 кв. минут	1	π/(2×180×60×60)² ≈ ≈ 1,87042315⋅10−12 полного угла
Полный угол =	4π ≈ ≈ 12,5663706 стерадиан	(2×180)²/π ≈ ≈ 41252,96125 кв. градусов	(2×180×60)²/π ≈ ≈ 1,48511066⋅108 кв. минут	(2×180×60×60)²/π ≈ ≈ 5,34638378⋅1011 кв. секунд	1

Для произвольной стягивающей поверхности S телесный угол Ω, под которым она видна из начала координат, равен

Ω=∫SdΩ=∬Ssin⁡ϑdφdϑ=∫S(r/r)⋅ndSr2,{\displaystyle \Omega =\int \limits _{S}d\Omega =\iint \limits _{S}\sin \vartheta \,d\varphi \,d\vartheta =\int \limits _{S}{\frac {(\mathbf {r} /r)\cdot \mathbf {n} dS}{r^{2}}},}

где r,ϑ,φ{\displaystyle r,\vartheta ,\varphi } — сферические координаты элемента поверхности dS,{\displaystyle dS,} r{\displaystyle \mathbf {r} } — его радиус-вектор, n{\displaystyle \mathbf {n} } — единичный вектор, нормальный к dS.{\displaystyle dS.}

1. Полный телесный угол (полная сфера) равен 4π стерадиан.
2. Сумма всех телесных углов, двойственных к внутренним телесным углам выпуклого многогранника, равна полному углу.

• Треугольник с координатами вершин r1{\displaystyle \mathbf {r} _{1}}, r2{\displaystyle \mathbf {r} _{2}}, r3{\displaystyle \mathbf {r} _{3}} виден из начала координат под телесным углом

Ω=2arctg(r1r2r3)r1r2r3+(r1⋅r2)r3+(r2⋅r3)r1+(r3⋅r1)r2,{\displaystyle \Omega =2\,\mathrm {arctg} \,{\frac {(\mathbf {r} _{1}\mathbf {r} _{2}\mathbf {r} _{3})}{r_{1}r_{2}r_{3}+(\mathbf {r} _{1}\cdot \mathbf {r} _{2})r_{3}+(\mathbf {r} _{2}\cdot \mathbf {r} _{3})r_{1}+(\mathbf {r} _{3}\cdot \mathbf {r} _{1})r_{2}}},}

где (r1r2r3){\displaystyle (\mathbf {r} _{1}\mathbf {r} _{2}\mathbf {r} _{3})} — смешанное произведение данных векторов, (ri⋅rj){\displaystyle (\mathbf {r} _{i}\cdot \mathbf {r} _{j})} — скалярные произведения соответствующих векторов, полужирным шрифтом обозначены векторы, нормальным шрифтом — их длины. Используя эту формулу, можно вычислять телесные углы, стянутые произвольными многоугольниками с известными координатами вершин (для этого достаточно разбить многоугольник на непересекающиеся треугольники).

• Телесный угол при вершине прямого кругового конуса с углом раствора α равен Ω=2π(1−cos⁡α2).{\displaystyle \Omega =2\pi \left(1-\cos {\frac {\alpha }{2}}\right).} Если известны радиус основания R{\displaystyle R} и высота H{\displaystyle H} конуса, то Ω=2π(1−HR2+h3).{\displaystyle \Omega =2\pi \left(1-{\frac {H}{\sqrt {R^{2}+H^{2}}}}\right).} Когда угол раствора конуса мал, Ω≈πα24{\displaystyle \Omega \approx {\frac {\pi \alpha ^{2}}{4}}} (угол α{\displaystyle \alpha } выражен в радианах), или Ω≈0,000239α2{\displaystyle \Omega \approx 0{,}000239\alpha ^{2}} (угол α{\displaystyle \alpha } выражен в градусах). Так, телесный угол, под которым с Земли видны Луна и Солнце (их угловой диаметр примерно равен 0,5°), составляет около 6⋅10⁻⁵ стерадиан, или ≈0,0005 % площади небесной сферы (то есть полного телесного угла).

• Телесный угол двугранного угла в стерадианах равен удвоенному значению двугранного угла в радианах.

Ω=4arctg⁡tg⁡(θs2)tg⁡(θs−θa2)tg⁡(θs−θb2)tg⁡(θs−θc2),{\displaystyle \Omega =4\,\operatorname {arctg} {\sqrt {\operatorname {tg} \left({\frac {\theta _{s}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{a}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{b}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{c}}{2}}\right)}},} где θs=θa+θb+θc2{\displaystyle \theta _{s}={\frac {\theta _{a}+\theta _{b}+\theta _{c}}{2}}} — полупериметр.

Через двугранные углы α,β,γ{\displaystyle \alpha ,\beta ,\gamma } телесный угол выражается как:

Ω=α+β+γ−π.{\displaystyle \Omega =\alpha +\beta +\gamma -\pi .}

• Телесный угол, под которым видна грань правильного N-гранника из его центра, равна 1N{\displaystyle {\frac {1}{N}}} полного телесного угла, или 4πN{\displaystyle {\frac {4\pi }{N}}} стерадиан.

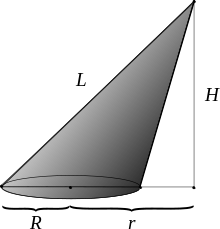• Телесный угол при вершине наклонного кругового конуса Телесный угол, под которым виден круг радиусом R из произвольной точки пространства (то есть телесный угол при вершине произвольного кругового конуса, не обязательно прямого) вычисляется с использованием полных эллиптических интегралов 1-го и 3-го рода^[1]:

Ω=2π+2HL(r−Rr+RΠ(α2,k)−K(k)){\displaystyle \Omega =2\pi +{\frac {2H}{L}}\left({\frac {r-R}{r+R}}\,\Pi (\alpha ^{2},k)-K(k)\right)} при r≤R,{\displaystyle r\leq R,}

Ω=2HL(r−Rr+RΠ(α2,k)−K(k)){\displaystyle \Omega ={\frac {2H}{L}}\left({\frac {r-R}{r+R}}\,\Pi (\alpha ^{2},k)-K(k)\right)} при r>R,{\displaystyle r>R,}

где K(k){\displaystyle K(k)} и Π(α2,k){\displaystyle \Pi (\alpha ^{2},k)} — полные нормальные эллиптические интегралы Лежандра 1-го и 3-го рода, соответственно;

r{\displaystyle r} — расстояние от центра основания конуса до проекции вершины конуса на плоскость основания;

H{\displaystyle H} — высота конуса;

L=h3+(r+R)2{\displaystyle L={\sqrt {H^{2}+(r+R)^{2}}}} — длина максимальной образующей конуса;

k=4rRL;{\displaystyle k={\frac {\sqrt {4rR}}{L}};}

α=4rRr+R.{\displaystyle \alpha ={\frac {\sqrt {4rR}}{r+R}}.}

Угол наклона крыши — как рассчитать и определить, формулы, видео

Угол наклона крыши является важнейшим параметром при возведении стропильной системы и расчете расхода кровельных материалов частного дома. Проектирование крыши – мероприятие весьма ответственное, которое следует доверить исключительно профессионалам, имеющим разрешение на проведение подобных работ. Однако в некоторых случаях, все предварительные расчеты можно сделать и самостоятельно, хотя бы для того, чтобы иметь представление о предполагаемом количестве материала и возможности реализации своих архитектурных идей. Из этой публикации вы узнаете, от чего зависит и как своими силами рассчитать угол наклона крыши, не прибегая к услугам дорогостоящих специалистов.

На что влияет уклон крыши

При самостоятельном возведении каркаса крыши большинство застройщиков руководствуется ее дизайном и назначением подкровельного пространства, что в корне неверно. На каркас крутых крыш практически не воздействует снеговая нагрузка, а это значит, что чисто теоретически можно сэкономить на сечении и шаге стропил. Однако ветер, оказывает наибольшее воздействие именно на кровли с крутыми скатами из-за их большой парусности, что уже на практике требует создания прочной стропильной системы.

Все это совершенно не значит, что пологие крыши лучше. На кровлях с малым уклоном снег будет задерживаться дольше, что создает внушительную нагрузку на стропильную систему. К тому же, угол ската крыши влияет на габариты чердачного помещения. Чем круче крыша – тем больше возможности у застройщика для обустройства жилой мансарды. Тем не менее не следует забывать о высокой стоимости конструкций с крутыми скатами, особенно в сравнении с пологими крышами. Сохранить объем чердачного пространства, не увеличивая высоту конька, поможет создание ломаной крыши.

Помимо снеговой и ветровой нагрузки на каркас оказывает влияние и вес кровельного пирога совместно с собственной массой стропильной системы. Если в кровле используются теплоизоляционные материалы, то и их вес учитывается при определении оптимального угла крыши.

В чем измеряется угол наклона крыши

Прежде всего, следует внести ясность в само понятие угол наклона. Данная величина – это угол, который образуется при пересечении горизонтальной плоскости (заложение) с плоскостью кровли. «Заложение» – это не что иное, как проекция ската крыши в горизонтальной плоскости.

В справочной литературе и специализированных таблицах в качестве единицы измерения угла наклона крыши используются проценты. Уклон кровли в процентах показывает отношение высоты подъема кровли (Н) к заложению (L).

В двускатных крышах (L) – это величина, равная длине половины пролета. L в односкатных крышах равняется длине пролета.

Правила расчета угла наклона кровли

Допустим, L = 3 м, а Н = 1 м. В таком случае отношение будет выглядеть, как Н к L или 1:3. Это простейший пример, показывающий большие неудобства в определении угла уклона таким способом.

Для простоты вычислений применяется специальная формула расчета угла наклона крыши, которая выглядит следующим образом.

I = H/L где:

• I – тангенс уклона ската;
• Н – высота подъема кровли;
• L – значение заложения.

Используем данные из примера выше. L = 3 м и Н = 1 м. Тогда, формула расчета выглядит, как I = 1/3 = 0,33. Теперь, для перевода значения тангенса острого угла в проценты необходимо полученное значение умножить на 100. Исходя из этого, получаем: 0,33 х 100 = 33%

Как определить угол наклона крыши в градусах? Перевести проценты в градусы можно двумя простыми способами:

• воспользоваться онлайн-конвертором;
• воспользоваться таблицами, опубликованными в специализированной справочной литературе.

Первый способ весьма прост, но требует подключения к интернету. В сети представлено огромное количество ресурсов, предоставляющих возможность воспользоваться онлайн-конвертором.

Таблицы уклона крыши в градусах и процентах найти значительно сложнее, однако они проще в применении. Публикуем таблицу соотношения проценты-градусы.

Определяем минимальный угол ската крыши в зависимости от кровельного материала

Исходя из крутизны скатов, все крыши условно делятся на четыре типа:

1. Высокие, с уклоном от 45 до 60°.
2. Скатные, с углом наклона кровли от 30 до 45°.
3. Пологие. Угол наклона скатов в таких конструкциях варьируется от 10 до 30°.
4. Плоские с уклоном до 10°.

Подходя к возведению крыши, застройщик планирует использование определенного кровельного материала. Следует учитывать, что далеко не каждый материал может быть использован на крышах с различным уклоном.

Далее рассмотрим зависимость между наиболее распространенными кровельными материалами и минимально допустимым углом ската крыши:

1. Асбоцементный шифер — 9° или 16%. Соотношение высоты подъема кровли к заложению 1:6.
2. Ондулин — 5°. Соотношение сторон 1:11.
3. Минимальный угол наклона односкатной крыши из металлочерепицы составляет 14°.
4. Керамическая черепица — 11°. Соотношение 1:6.
5. Цементно-песчаная черепица — 34° или 67%. Соотношение высоты кровли к заложению 1:1,5.
6. Битумная черепица — 11°. Соотношение сторон 1:5.
7. Профнастил — 12° При меньшем уклоне необходимо провести обработку стыков герметизирующим средством.
8. Оцинковка и стальные листы требуют минимального уклона 17°.
9. Рулонные битумные материалы — 3°.
10. Наплавляемая кровля может быть использована в качестве покрытия крыши с уклоном 15%.

В проектировании крыш существует понятие – максимальный угол наклона скатов. Данное значение является критическим для использования конкретного материала. На рисунке ниже показаны минимальные и максимальные значения угла наклона крыши для некоторых распространенных кровельных материалов. Кроме этого, в последней колонке собраны данные о том, какой уклон ската чаще всего используется для данных материалов отечественными застройщиками.

Как видно из приведенной таблицы, между минимальным и максимальным углом наклона крыши весьма солидный разрыв.

Выбирая уклон из диапазона допустимых значений, следует руководствоваться исключительно эстетическими соображениями и расходом материала.

Снеговые и ветровые нагрузки

При проектировании кровли всегда учитываются снеговые и ветровые нагрузки на стропильную систему. Чем круче скаты, тем меньше снега на них задержится.

Для правильного вычисления необходимой прочности конструкции вводится поправочный коэффициент:

1. Для крыш с уклоном менее 25° применяется коэффициент равный 1.
2. Стропильные конструкции со скатами от 25 до 60° требуют применения коэффициента 0,7.
3. Кровли, выполненные с углом наклона скатов более 60°, не требуют применения коэффициента, так как снег на них практически не задерживается.

Для простоты вычислений используют карты, в которых отмечены средние значения снеговой нагрузки по регионам РФ.

Примеры расчета

Правила проведения расчетов просты: находим свой регион, определяем снеговую нагрузку, выделенную своим цветом, принимаем в расчет первое значение, умножаем на поправочный коэффициент исходя из предполагаемого угла уклона крыши. В качестве наглядного примера рассчитаем снеговую нагрузку для крыши дома в Норильске углом наклона скатов 35°. Итак, 560 кг/м² умножаем на коэффициент 0,7. Получаем снеговую нагрузку для данного региона и конкретной конструкции кровли 392 кг/м².

Для определения ветровых нагрузок также используются карты, в которых отмечены расчетные значения ветровых нагрузок по регионам.

Кроме этого, в расчетах следует учитывать:

1. Розу ветров, а конкретно – расположение дома на местности и относительно других строений.
2. Высоту постройки.

По типу расположения дома на местности, все строения можно разделить на три группы:

1. А – постройки, расположенные не открытой местности.
2. Б – Строения, расположенные в населенных пунктах с ветровой преградой не выше 10 м.
3. В – здания, находящиеся в населенных пунктах с ветровой преградой от 25 м.

В зависимости от зоны размещения и высоты строения при проектировании крыши вводятся поправочные коэффициенты, учитывающие ветровую нагрузку. Все факторы, влияющие на ветровую нагрузку, сведены в таблицу, по которой легко сделать расчет.

Например: для одноэтажного дома в Норильске ветровая нагрузка составит: 84 кг/м² умноженная на коэффициент 0,5, соответствующий зоне «В», что составляет 42 кг/м².

Помимо этого, учитываются аэродинамические нагрузки, воздействующие на стропильную систему и кровельный материал. В зависимости от направления ветра, нагрузку условно делят на зоны, которые предполагают различные поправочные коэффициенты.

Для обеспечения запаса прочности рекомендуется брать значения из наиболее нагруженных зон G и H.

Видео-урок по нахождению высоты и наклона крыши

1.7 Измерение углов наклона

1.7.1 Вертикальный круг теодолита

С помощью теодолита можно измерять не только горизонтальные углы, но и углы наклона, т.е. вертикальные углы  между на­правлением линии визирования и горизонтальной плоскостью. Различаются положительные и отрицательные углы наклона: угол имеет знак плюс, если линия визирования повыша­ется относительно горизонта трубы, и минус – при ее понижении (рис. 1.13).

Измерение углов наклона производится с помощью вер­тикального круга теодолита (рис. 1.14). Это — угломерный круг 1, жёстко скрепленный со зрительной трубой 2 и вращающийся вместе с ней. Алидада 3 вертикального круга при измерениях остается неподвижной. На алидаде точных теодолитов укреплен цилиндрический уровень 4, кон­тролирующий неизменность положения алидады при измерениях. У некоторых теодолитов этот уровень заменен компенсатором, а у теодолита Т30 и 2Т30П он вообще отсутствует. Поэтому при измерениях углов наклона этими теодолитами необходимо тщательно нивелировать прибор.

Верти­кальный круг теодолита Т30 оцифрован от 0 до 360° про­тив хода часовой стрелки. Начальный диаметр лимба 0-180° должен распола­гаться параллельно визирной оси трубы, и при горизонтальном ее положении при КЛ отсчет повертикальному кругу должен быть 0°00.

Этот отсчет может несколько отличаться от нуля на величи­ну, называемую местом нуля (МО). Местом нуля называется отсчет по вертикальному кругу при КЛ, соответствующий гори­зонтальному положению визирной оси трубы и оси уровня при али­даде. При измерениях углов наклона на точки наводят горизонтальной нитью сетки вблизи вертикальной нити (рис. 1.15). Перекрестием сетки нитей наводить на точки не рекомендуется.

1.7.2 Поверка места нуля

Если теодолитом планируют измерять вертикальные углы, то делают ещё одну (пятую) поверку — поверку места нуля (МО) вертикального круга теодолита.

Условие. Начальный диаметр вертикального круга (0°-180° для теодолита Т30 или 0°-0° для теодолита 2Т30П) должен распола­гаться параллельно визирной оси трубы, и при горизонтальном ее положении при КЛ отсчет по вертикальному кругу должен быть 0°00.

Выполнение. Зрительную трубу дважды при КЛ и КП наводят горизонтальной нитью на хорошо видимую точку и снимают отсчёты Л и П по вертикальному кругу. Вычисляют место нуля по формуле (1.14) или (1.15).

Допуск. Место нуля по абсолютной величине не должно превышать 2t.

Исправление. Если допуск не соблюдается, место нуля исправляют. Для этого находят «правильны отсчет

или . (1.13)

Этот отсчет устанавливают (для теодолитов ТЗО и 2ТЗОП) вра­щением наводящего винта трубы. Горизонтальная нить сетки при этом сместится с визирной цели. Затем вертикальными исправи­тельными винтами сетки нитей вновь совмещают горизонтальную нить с визирной целью.

Для теодолитов с уровнем при алидаде вертикального круга исправление места нуля производят иначе. Правильный отсчет устанавливают наводящим винтом уровня. Пузырек уровня при этом сместится с нульпункта. Его возвращают в нульпункт исправи­тельными винтами уровня.

После исправления места нуля определение его повторяют заново. Если исправление производилось исправительными винтами сетки, то заново повторяют поверку коллимационной ошибки (п.1.4.2) и поверку положения сетки нитей (п. 1.4.4).

Градус (геометрия) — Википедия

У этого термина существуют и другие значения, см. Градус.

Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.

Окружность с хордой, образованной стороной равностороннего треугольника (выделена красным). Одна шестидесятая этой дуги равна одному градусу. Шесть таких хорд охватывают полный круг.

Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.

Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году^[1]. Некоторые древние календари, такие как древнеперсидский, использовали год в 360 дней.

Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления^[2][3].

Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.

Градус в альтернативных единицах измерения:

1∘=2π360{\displaystyle 1^{\circ }={\frac {2\pi }{\displaystyle {360}}}} радиан =π180=1p≈157,295779513∘{\displaystyle ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}}^[4]≈0,0174532925{\displaystyle \approx 0{,}0174532925} (радиан в 1°)

1∘=1360{\displaystyle 1^{\circ }={\frac {1}{360}}} оборота=0,002(7) оборота=0,002777777777…

1∘=400360{\displaystyle 1^{\circ }={\frac {400}{360}}} градов=1,(1) градов=1,11111111111… градов

По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением тремя штрихами — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей^[5]; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).

Минуты и секунды в других системах измерения:

1′=2π360∘⋅60′=1′p′≈1′3437,747′{\displaystyle 1’={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60′}}={\frac {1′}{p’}}\approx {\frac {1′}{3437{,}747′}}}^[4]≈2,90888208⋅10−4 rad{\displaystyle \approx 2{,}90888208\cdot 10^{-4}~{\text{rad}}} (1 минута в радианах)

1″=2π360∘⋅60′⋅60″=1″p″≈1″206264,8″{\displaystyle 1»={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60’\cdot 60»}}={\frac {1»}{p»}}\approx {\frac {1»}{206264{,}8»}}}^[4]≈4,848136811⋅10−6 rad{\displaystyle \approx 4{,}848136811\cdot 10^{-6}~{\text{rad}}} (1 секунда в радианах).

Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.

Угловая секунда[править | править код]

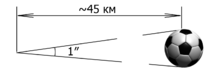
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги^[6]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла^[7].

Использование[править | править код]

Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается ^s). Соотношение между этими величинами определяется формулой 1^s=15″.^[8]

Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой^[6][9], что является простой транслитерацией с англ. arcsecond.

Дольные единицы[править | править код]

По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению^[7]. Однако согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками^[10], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).

Связь различных угловых единиц измерения

Единица	Величина	Обозначение	Аббревиатура	Радиан (прибл.)
градус	1/360 окружности	°	deg	17,4532925 mrad
минута	1/60 градуса	′	arcmin, amin, ′^{\displaystyle {\hat {‘}}}, MOA	290,8882087 µrad
секунда	1/60 минуты	″	arcsec	4,8481368 µrad
миллисекунда	1/1000 секунды		mas	4,8481368 nrad
микросекунда	1 × 10−6 секунды		μas	4,8481368 prad

Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.

Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.^{[источник не указан 2770 дней]}

В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP)^[11][12].

1. ↑ Weisstein, Eric W. Degree (англ.). Wolfram MathWorld. Дата обращения 26 ноября 2017.
2. ↑ James Hopwood Jeans. The Growth of Physical Science. — 1947. — С. 7.
3. ↑ Murnaghan, Francis D. Analytic geometry. — New York: Prentice-Hall, inc., 1946. — P. 2.
4. ↑ ^{1 2 3} Переводные множители — <57,295779513>, <3437,747>, <206264,8> — см. Радиан#Связь радиана с другими единицами.
5. ↑ Боголюбов, 1983, с. 393—394.
6. ↑ ^{1 2} Англо-русско-английский астрономический словарь (неопр.). Astronet. Дата обращения 23 декабря 2007.
7. ↑ ^{1 2} Non-SI units accepted for use with the International System of Units (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
8. ↑ Справочник. Некоторые внесистемные единицы (неопр.). ASTROLAB. Дата обращения 23 декабря 2007.
9. ↑ Glossary entry for English term «arcsecond» (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
10. ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003. Архивировано 5 августа 2013 года.
11. ↑ Гурьянов С. Почему звезды называются именно так? (неопр.). проект «Астрогалактика» (29 октября 2005 года). Дата обращения 26 декабря 2007.
12. ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.