Гидравлическое сопротивление. Расчет в Excel.
Опубликовано 24 Июн 2018
Рубрика: Теплотехника | 19 комментариев
Выполнение расчета гидравлического сопротивления отдельного трубопровода и всей системы в комплексе является ключевой задачей в гидравлике, решение которой позволяет подобрать сечения труб и насос с необходимыми значениями давления и расхода в рабочем режиме.
В одной из ранних статей на блоге рассмотрен простой пример расчета трубопровода с параллельными участками с использованием понятия «характеристика сопротивления». В конце статьи я анонсировал: «Можно существенно повысить точность метода…». Под этой фразой подразумевалось учесть зависимость характеристик сопротивления от расхода более точно. В том расчете характеристики сопротивлений выбирались из таблиц по диаметру трубы и по предполагаемому расходу. Полковов Вячеслав Леонидович написал взамен таблиц пользовательские функции в Excel для более точного вычисления гидравлических сопротивлений, которые любезно предоставил для печати. Термины «характеристика сопротивления» и «гидравлическое сопротивление» обозначают одно и то же.
Краткая теория.
В упомянутой выше статье теория вкратце рассматривалась. Освежим в памяти основные моменты.
Движение жидкостей по трубам и каналам сопровождается потерей давления, которая складывается из потерь на трение по длине трубопровода и потерь в местных сопротивлениях – в изгибах, отводах, сужениях, тройниках, запорной арматуре и других элементах.
В гидравлике в общем случае потери давления вычисляются по формуле Вейсбаха:
∆Р=ζ·ρ·w²/2, Па, где:
- ζ – безразмерный коэффициент местного сопротивления;
- ρ – объёмная плотность жидкости, кг/м
- w – скорость потока жидкости, м/с.
Если с плотностью и скоростью всё более или менее понятно, то определение коэффициентов местных сопротивлений – достаточно непростая задача!
Как было отмечено выше, в гидравлических расчетах принято разделять два вида потерь давления в сетях трубопроводов.
- В первом случае «местным сопротивлением» считается трение по длине прямого участка трубопровода. Перепад давления для потока в круглой трубе рассчитывается по формуле Дарси-Вейсбаха:
∆Ртр=ζтр·ρ·w²/2=λ·L·ρ·w²/(2·D), Па, где:
- D – внутренний диаметр трубы, м;
- λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси).
Таким образом, при учете сопротивления трению коэффициент потерь – коэффициент местного сопротивления – и коэффициент гидравлического трения связаны для круглых труб зависимостью:
ζтр=λ·L/D
- Во втором случае потери давления в местных сопротивлениях вычисляются по классической формуле Вейсбаха:
∆Рм=ζм·ρ·w²/2, Па
Коэффициенты местных сопротивлений определяются для каждого вида «препятствия» по индивидуальным эмпирическим формулам, полученным из практических опытов.
Выполним ряд математических преобразований. Для начала выразим скорость потока через массовый расход жидкости:
w=G/(ρ·π·D²/4), м/с, где:
- G – расход жидкости, кг/с;
- π – число Пи.
Тогда:
∆Ртр=8·λ·L·G²/(ρ·π²·D5), Па;
∆Рм=8·ζм·G²/(ρ·π²·D4), Па.
Введем понятие гидравлических сопротивлений:
Sтр=8·λ·L·/(ρ·π²·D5), Па/(кг/с)²;
Sм=8·ζм·/(ρ·π²·D4), Па/(кг/с)².
И получим удобные простые формулы для вычисления потерь давления при прохождении жидкости в количестве G через эти гидравлические сопротивления:
∆Ртр=Sтр·G², Па;
∆Рм=Sм·G², Па.
Размерность гидравлического сопротивления (Па/(кг/с)²) определена массовой скоростью (кг/с) движения жидкости, а физические процессы в транспортных системах зависят от её объёмной скорости (м
Для удобства последующих расчётов целесообразно введение понятия «гидравлическая проводимость» — а.
Для последовательного и параллельного соединений гидравлических сопротивлений справедливы формулы:
Sпосл=S1+S2+…+Sn, Па/(кг/с)²;
Sпар=1/(а1+a2+…+an)², Па/(кг/с)²;
ai=(1/Si)0,5, (кг/с)/Па0,5.
Коэффициент гидравлического трения.
Для определения гидравлического сопротивления от трения о стенки трубы Sтр необходимо знать параметр Дарси λ – коэффициент гидравлического трения по длине.
В технической литературе приводится значительное количество формул разных авторов, по которым выполняется вычисление коэффициента гидравлического трения в различных диапазонах значений числа Рейнольдса.
Обозначения в таблице:
- Re – число Рейнольдса;
- k – эквивалентная шероховатость внутренней стенки трубы (средняя высота выступов), м.
В [1] приведена еще одна интересная формула расчета коэффициента гидравлического трения:
λ=0,11·[(68/Re+k/D+(1904/Re)14)/(115·(1904/Re)10+1)]0,25
Вячеслав Леонидович выполнил проверочные расчеты и выявил, что вышеприведенная формула является наиболее универсальной в широком диапазоне чисел Рейнольдса!
Значения, полученные по этой формуле чрезвычайно близки значениям:
- функции
- функции λ=0,11·(68/Re+k/D)0,25для зоны турбулентного характера потока при Re>4500;
- в диапазоне 1500<Re<4500 согласно анализу присутствует переходная зона.
В переходной зоне, согласно опытам Никурадзе, график функции λ=f(Re,D,k) имеет сложную форму. Он представляет собой две сопряженные обратные кривые, которые в свою очередь сопрягаются с одной стороны с кривой гладких труб (ламинарный поток), а с другой стороны с прямыми относительной шероховатости.
Данная зона до конца не изучена, поэтому желательно гидравлические режимы проектируемых систем рассчитывать без захода в эту область: 1500<Re<4500!
На следующем рисунке показаны графики функции λ=f(Re,D,k), построенные по вышеприведенной универсальной формуле. Характер кривых в переходной области соответствует графикам Никурадзе [2, 4].
Пользовательская функция в Excel КтрТрубаВода(Рвода,tвода,G,D,kэ) выполняет расчет коэффициента гидравлического трения
Внимание!
- В зоне переходного характера потока происходит смена знака наклона кривой λ, что может вызвать неработоспособность систем автоматического регулирования!
- ПФ КтрТрубаВода(Pвода,tвода,G,D,kэ) при турбулентном потоке существенно зависит от значения kэ – эквивалентной шероховатости внутренней поверхности трубы. В связи с этим следует обращать внимание на задание объективного значения kэ с учётом используемых при монтаже труб (см. [2] стр.78÷83).
Расчет в Excel гидравлических сопротивлений.
Для облегчения выполнения рутинных гидравлических расчетов Полковов В.Л. разработал ряд пользовательских функций. Перечень некоторых из них, наиболее часто используемых на практике, приведен в таблице ниже.
Некоторые пояснения по аргументам пользовательских функций:
- ГСдиффузор(Pвода,tвода,G,Dmin,Dmax,kэ,L) – свободные размеры;
- ГСпереходДиффузор(Pвода,tвода,G,Dmin,Dmax,kэ) – стандартный переход;
- ГСконфузор(Pвода,tвода,G,Dmin,Dmax,kэ,L) – свободные размеры;
- ГСпереходКонфузор(P
- ГСотвод(Pвода,tвода,G,D0,R0,Угол,kэ) – свободные размеры;
- ГСотводГОСТ(Pвода,tвода,G,D,Угол,kэ) – стандартный отвод.
Приведённые пользовательские функции желательно использовать с учётом начального участка транспортирования (расстояния от одного гидравлического сопротивления до следующего гидравлического сопротивления). Это позволяет уменьшить погрешности расчётов, вызванных влиянием «неустановившегося» характера потока жидкости.
Для турбулентных течений длина начального участка должна быть не менее:
Lнач=(7,88·lg (Re) – 4,35)·D
Для ламинарных течений минимальная длина начального участка:
Lнач=B·Re·D
Здесь В=0,029 по данным Буссинекса, и В=0,065 по данным Шиллера, D — внутренний диаметр системы транспортирования.
Далее на скриншоте показана таблица в Excel с примерами расчетов гидравлических сопротивлений.
Литература:
- Черникин А.В. Обобщение расчета коэффициента гидравлического сопротивления трубопроводов // Наука и технология углеводородов. М.: 1998. №1. С. 21–23.
- И.Е. Идельчик, «Справочник по гидравлическим сопротивлениям». 3-е издание, переработанное и дополненное. Москва, «Машиностроение», 1992.
- А.Д. Альтшуль, «Гидравлические сопротивления», издание второе, переработанное и дополненное. Москва, «НЕДРА», 1982.
- Б.Н. Лобаев, д.т.н., профессор, «Расчёт трубопроводов систем водяного и парового отопления». Государственное издательство литературы по строительству и архитектуре. УССР, Киев, 1956.
Ссылка на скачивание файла: gidravlicheskie-soprotivleniya (xls 502,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Гидравлическое сопротивление
Содержание
Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:
Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.
Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.
Коэффициент гидравлического сопротивления
Гидравлические потери выражают либо в потерях напора Δh в линейных единицах столба среды, либо в единицах давления ΔP:
Δh= ΔP/(ρg)
где ρ — плотность среды, g — ускорение свободного падения.
В производственной практике перемещение жидкости в потоках связано с необходимостью преодолеть гидравлическое сопротивление трубы по длине потока, а также различные местные сопротивления: Поворотов
Поворотов Диафрагм
Диафрагм Задвижек
Задвижек Вентилей
Вентилей Кранов
Кранов Различных ответвлений и тому подобного
Различных ответвлений и тому подобного
На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.
Аналитически потери напора на местные гидравлические сопротивления выражаются в виде.
hr = ξ υ2 / (2g)
где ξ – коэффициент местного сопротивления (обычно определяется опытным путем).
Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений коэффициента гидравлического сопротивления, таблиц, эмпирических формул, диаграмм и т.д.
Исследование потерь энергии (потери напора насоса), обусловленных различными местными сопротивлениями, ведутся уже более ста лет. В результате экспериментальных исследований, проведенных в России и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных задач. Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.
В этой статье будут рассмотрены некоторые характерные местные сопротивления, часто встречающиеся на практике.
Местные гидравлические сопротивления
Как уже было написано выше, потери напора во многих случаях определяются опытным путем. При этом любое местное сопротивление похоже на сопротивление при внезапном расширении струи. Для этого имеется достаточно оснований, если учесть, что поведение потока в момент преодоления им любого местного сопротивления связано с расширением или сужением сечения.
Гидравлические потери на внезапное сужение трубы
Сопротивление при внезапном сужении трубы сопровождается образованием в месте сужения водоворотной области и уменьшения струи до размеров меньших, чем сечение малой трубы. Пройдя участок сужения, струя расширяется до размеров внутреннего сечения трубопровода. Значение коэффициента местного сопротивления при внезапном сужении трубы можно определить по формуле.
ξвн. суж = 0,5(1- (F2/F1))
Значение коэффициента ξвн. суж от значения отношения (F2/F1)) можно найти в соответствующем справочнике по гидравлике.
Гидравлические потери при изменении направления трубопровода под некоторым углом
В этом случае вначале происходит сжатие, а затем расширение струи вследствие того, что в месте поворота поток по инерции как бы отжимается от стенок трубопровода. Коэффициент местного сопротивления в этом случае определяется по справочным таблицам или по формуле
ξ поворот = 0,946sin(α/2) + 2.047sin(α/2)2
где α – угол поворота трубопровода.
Местные гидравлические сопротивления при входе в трубу
В частном случае вход в трубу может иметь острую или закругленную кромку входа. Труба, в которую входит жидкость, может быть расположена под некоторым углом α к горизонтали. Наконец, в сечении входа может стоять диафрагма, сужающая сечение. Но для всех этих случаев характерно начальное сжатие струи, а затем её расширение. Таким образом и местное сопротивление при входе в трубу может быть сведено к внезапному расширению струи.
Если жидкость входит в цилиндрическую трубу с острой кромкой входа и труба наклонена к горизонту под углом α, то величину коэффициента местного сопротивления можно определить по формуле Вейсбаха:
ξвх = 0,505 + 0,303sin α + 0,223 sin α2
Местные гидравлические сопротивления задвижки
На практике часто встречается задача расчета местных сопротивлений, создаваемых запорной арматурой, например, задвижками, вентилями, дросселями, кранами, клапанами и т.д. В этих случаях проточная часть, образуемая разными запорными приспособлениями, может иметь совершенно различные геометрические формы, но гидравлическая сущность течения при преодолении этих сопротивлений одинакова.
Гидравлическое сопротивление полностью открытой запорной арматуры равно
ξвентиля = от 2,9 до 4,5
Величины коэффициентов местных гидравлических сопротивлений для каждого вида запорной арматуры можно определить по справочникам.
Гидравлические потери диафрагмы
Процессы, происходящие в запорных устройствах, во многом похожи на процессы при истечении жидкости через диафрагмы, установленные в трубе. В этом случае также происходит сужение струи и последующее её расширение. Степень сужения и расширения струи зависит от ряда условий:  режима движения жидкости
режима движения жидкости отношения диаметров отверстия диафрагмы и трубы
отношения диаметров отверстия диафрагмы и трубы конструктивных особенностей диафрагмы.
конструктивных особенностей диафрагмы.
Для диафрагмы с острыми краями:
ξдиафр = d02 / D02
Местные гидравлические сопротивления при входе струи под уровень жидкости
Преодоление местного сопротивления при входе струи под уровень жидкости в достаточно большой резервуар или в среду, не заполненную жидкостью, связано с потерей кинетической энергии. Следовательно, коэффициент сопротивления в этом случае равен единице.
ξвхода = 1
Видео о гидравлическом сопротивлении
На преодоление гидравлических потерь затрачивается работа различных устройств (насосов и гидравлических машин)
Для снижения влияния гидравлических потерь рекомендуется в конструкции трассы избегать использования узлов способствующих резким изменениям направления потока и стараться применять в конструкции тела обтекаемой формы.
Даже применяя абсолютно гладкие трубы приходится сталкиваться с потерями: при ламинарном режиме течения(по Рейнольдсу) шероховатость стенок не оказывает большого влияния, но при переходе к турбулентному режиму течения как правило возрастает и гидравлическое сопротивление трубы.
6. Гидравлический расчет трубопроводов
6.1. Классификация трубопроводов
Рассмотрим классификацию трубопроводов по следующим
характерным признакам:
По функциональному назначению трубопроводы подразделяют на
– всасывающие;
– нагнетательные.
С конструктивной точки зрения трубопроводы подразделяют на:
– простые;
– сложные;
– короткие;
– длинные.
Простыми называют трубопроводы, не имеющие ответвлений и обслуживающие только одну точкуx.
Причем, диаметр трубы, а также расход жидкости на всей длине трубы остается неизменным.
Сложныетрубопроводы делятся на тупиковые, параллельные и кольцевые.
Тупиковые состоят из магистрального (главного) трубопровода, от которого в разные стороны отходят ответвления к потребителям.
Параллельные состоят из нескольких параллельно проложенных трубопроводов, связанных между собой перемычками с регулирующими задвижками.
Кольцевые представляют собой замкнутую сеть труб, что обеспечивает подачу воды в любом направлении.
При аварии на каком-либо участке подача воды потребителю не прекращается.
Короткими называют трубопроводы, которые имеют значительные местные сопротивления по сравнению с линейными (путевыми).
Длинными называют трубопроводы, у которых доминируют потери напора по длине трубопровода; местными потерями и скоростным напором пренебрегают.
6.2. Система уравнений и задачи гидравлического расчета трубопроводов
Гидравлический расчет трубопроводов основан на следующих уравнениях, формулах и зависимостях:
– уравнение Бернулли для потока вязкой жидкости
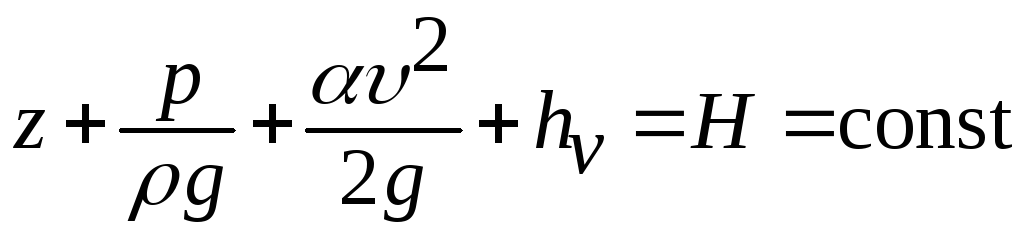 ; (6.1)
; (6.1)
– уравнение неразрывности для установившегося потока жидкости
(уравнение расхода):
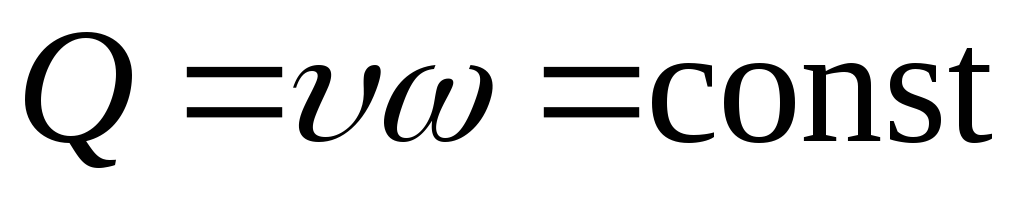 ; (6.2)
; (6.2)
– формула Дарси-Вейсбаха для учета потерь на трение (по длине трубопровода):
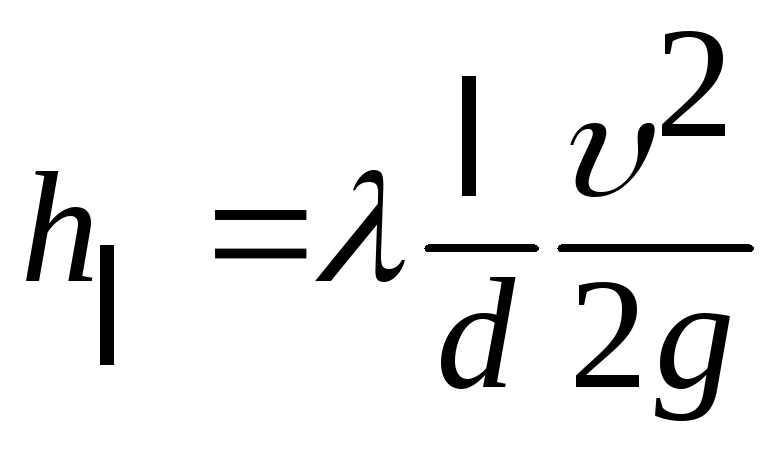 ; (6.3)
; (6.3)
– формула для учета местных потерь:
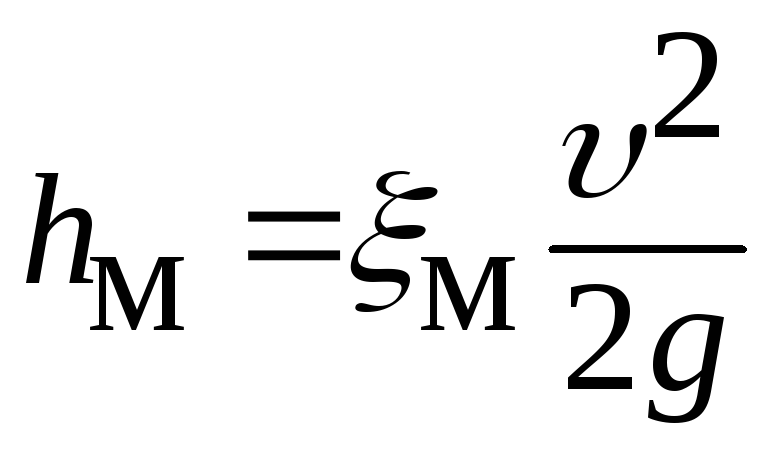 ; (6.4)
; (6.4)
– формула Шези при расчете длинных трубопроводов:
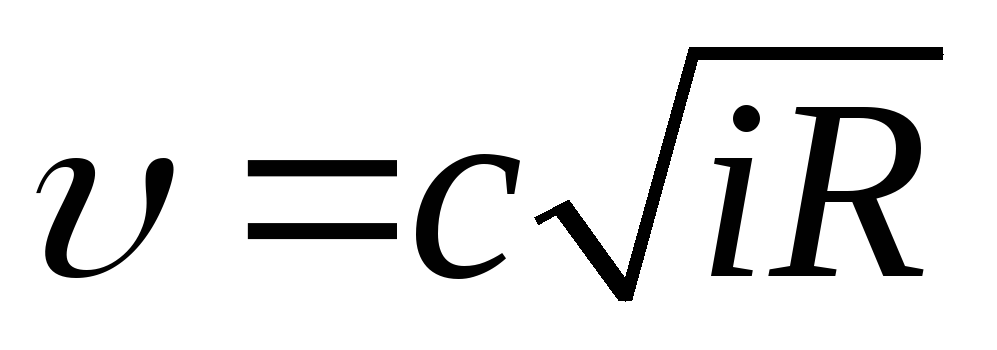 или
или  , (6.5)
, (6.5)
где | коэффициент Шези; |
n– | коэффициент шероховатости; |
R– | гидравлический радиус; |
y– | показатель степени, у = f(n, R). |
Обозначим в формуле (6.5)
через 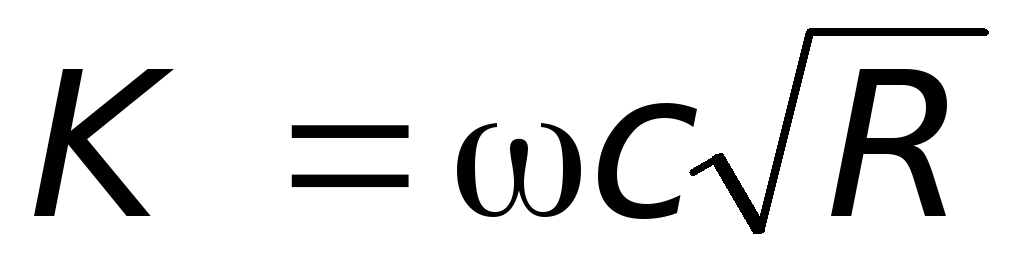 ,
получим
,
получим
 , (6.6)
, (6.6)
где K– | расходная характеристика (модуль расхода), представляющая собой расход при гидравлическом уклоне, равном единице; |
– формула для определения гидравлического уклона (удельных потерь напора по длине):
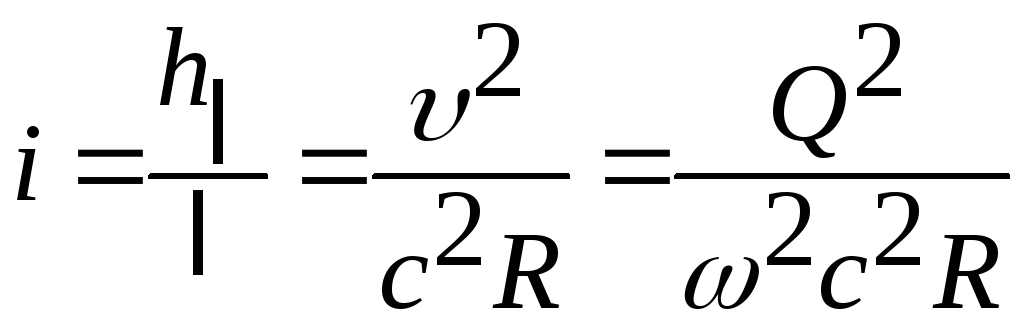 (6.7)
(6.7)
или по формуле Дарси-Вейсбаха (6.3):
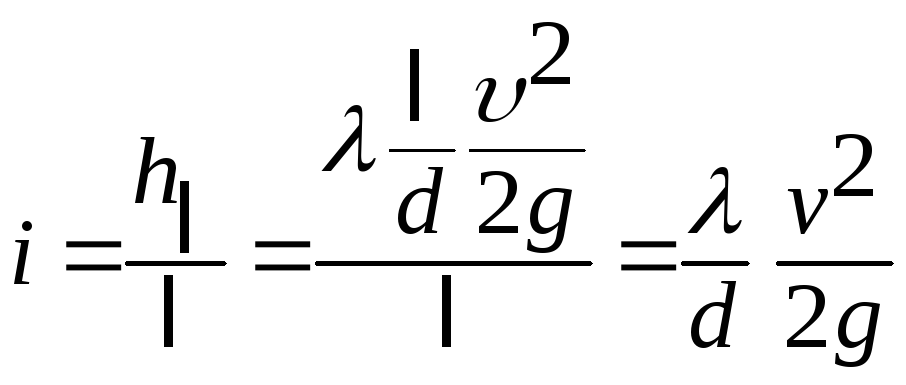 .
.
Заменяя скорость на расходQ, из уравнения расхода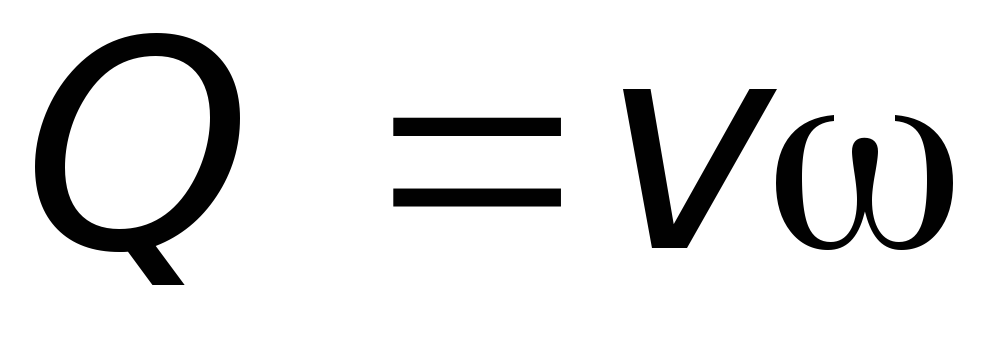 получим
получим
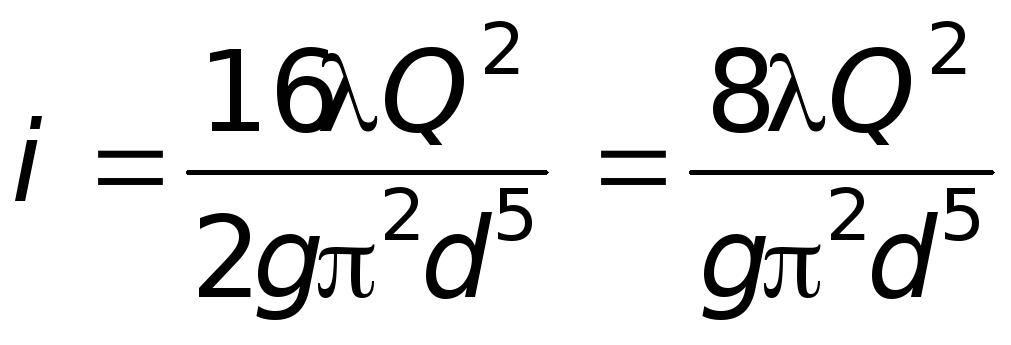 . (6.8)
. (6.8)
Обозначим  – удельное сопротивление трубопровода,
получим
– удельное сопротивление трубопровода,
получим
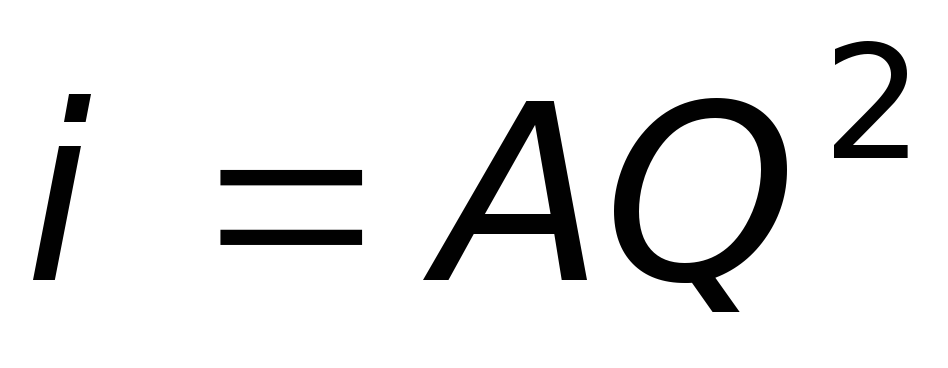 . (6.9)
. (6.9)
Тогда
 , (6.9а)
, (6.9а)
где S– | линейное сопротивление трубопровода. |
Найдем связь между K иAиз формул (6.6 и 6.8):
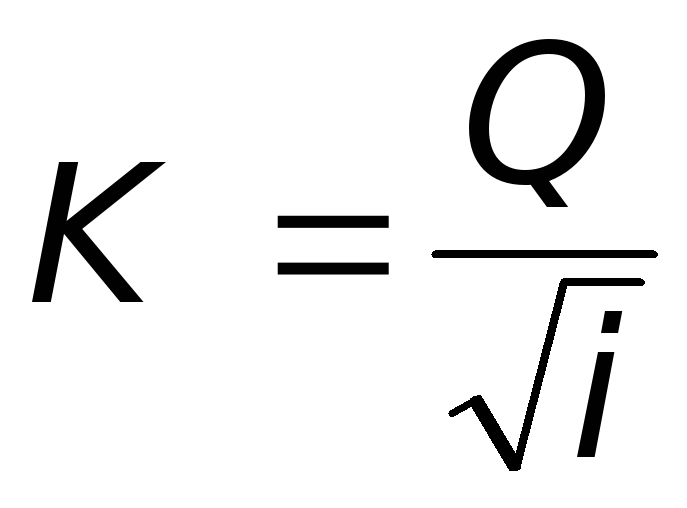 или
или 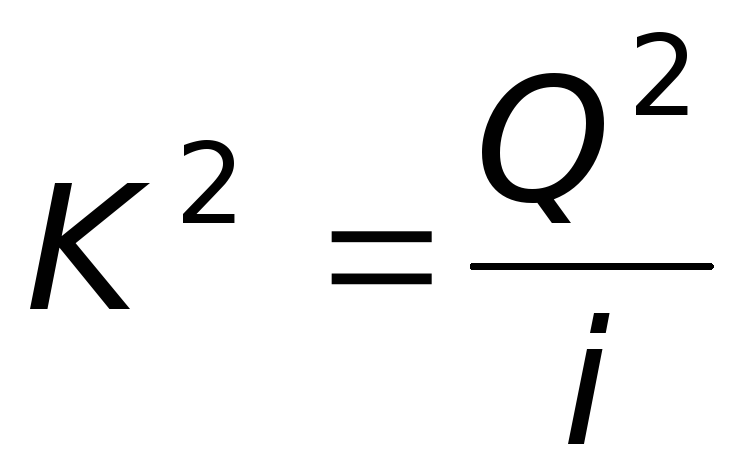 .
.
Подставляя значение i из формулы (6.8), получим
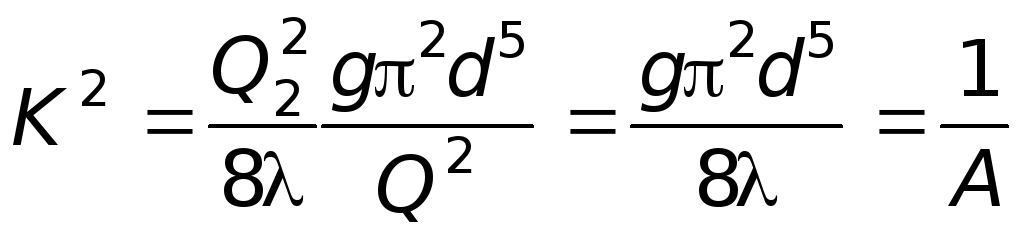 . (6.10)
. (6.10)
Из выражений (6.10 и 6.9), находим
 . (6.11)
. (6.11)
Тогда потери по длине определяются по формуле
 . (6.12)
. (6.12)
Учитывая, что 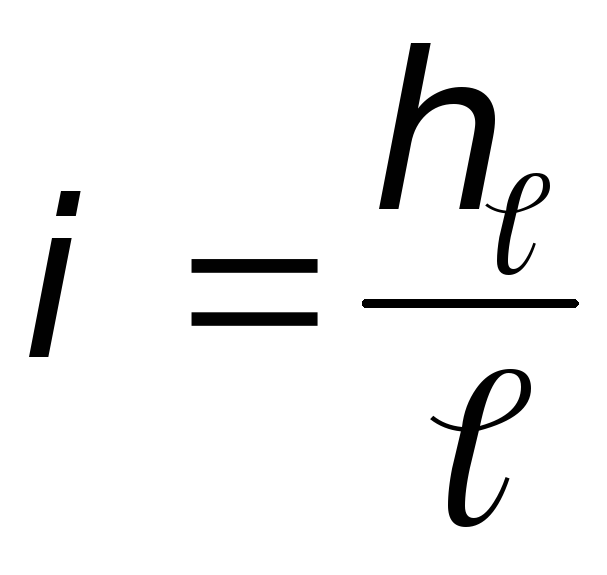 ,
получим
,
получим
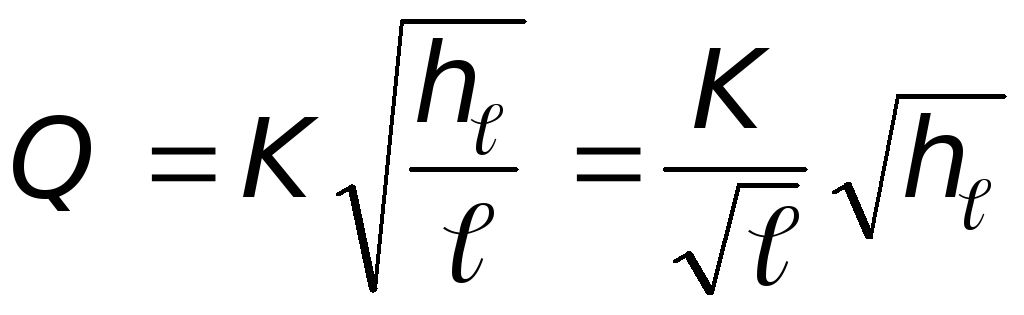 .
.
Обозначим 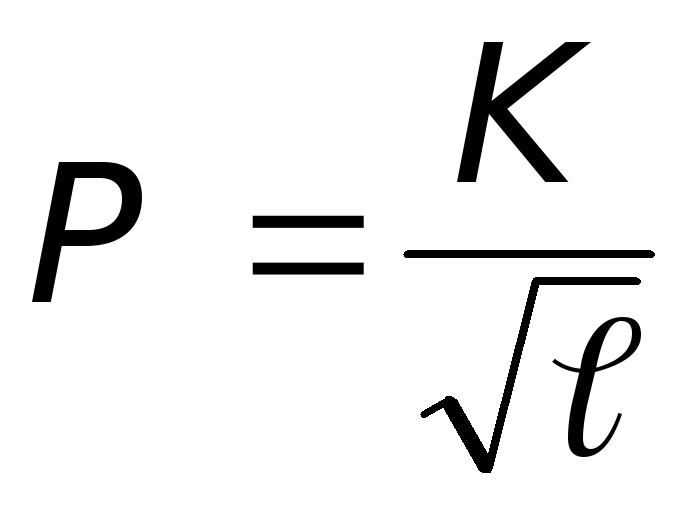 ,
получим:
,
получим:
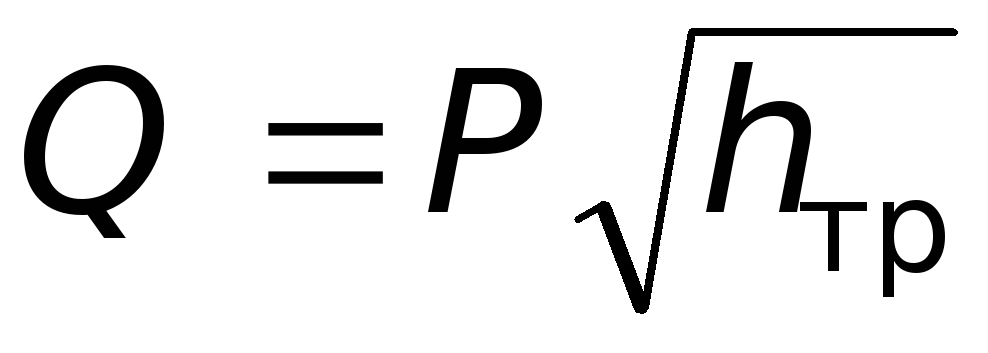 , (6.13)
, (6.13)
где Р– | проводимость, выражающая собой расход жидкости при hтр = 1. |
Сравнивая выражения (6.9) и (6.13), найдем связь между P и S.
Из выражения (6.9а) имеем 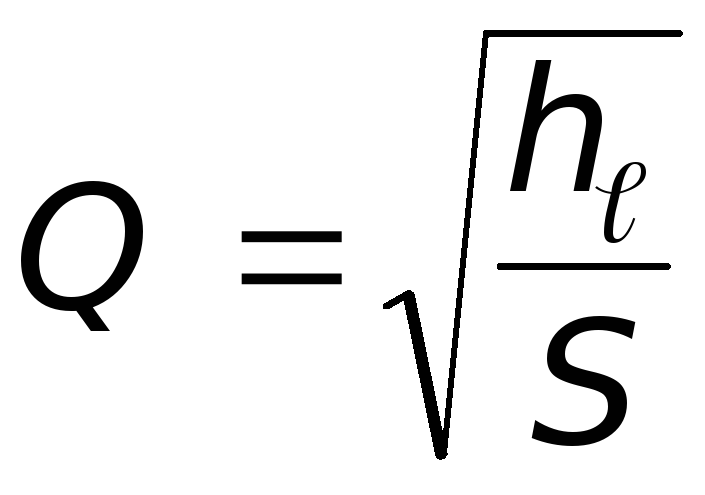 ,
,
тогда:
 или
или 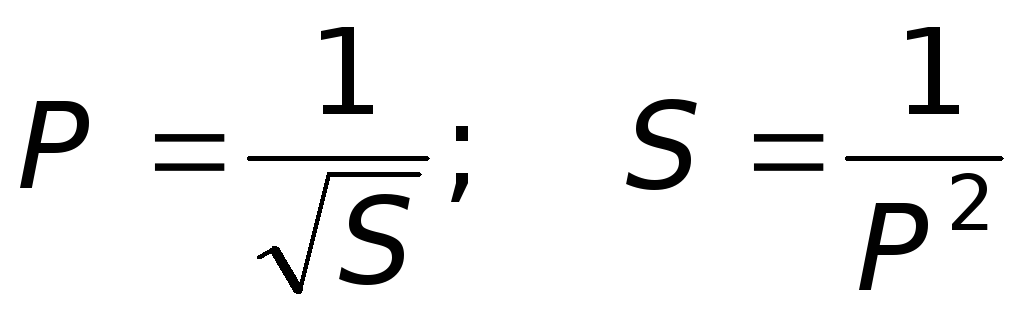 . (6.14)
. (6.14)
Значения AиKприводятся в таблицах.
Общая задача гидравлического расчета трубопроводов заключается в определении диаметров труб для пропуска заданного расхода воды и напора, необходимого для подачи воды ко всем точкам водоразбора при оптимальных затратах.
Оптимальные затраты учитывают расход средств на строительство и эксплуатацию трубопровода.
Например, если принять при расчете высокие скорости движения воды, то за счет этого уменьшаются диаметры труб, но увеличиваются потери напора по длине, что приводит в процессе эксплуатации к большим затратам электроэнергии.
Рекомендации по выбору оптимальных скоростей движения жидкости в трубопроводах приводятся в СНиПах.
При решении инженерных задач четыре величины – расход Q, скоростьv, диаметр трубопроводаdи потери напораh– являются переменными и взаимозависимыми.
Их связывают между собой уравнения Бернулли и неразрывности (расхода), потери по длине трубопровода и на местных сопротивлениях, которые учитываются по формулам (6.3 и 6.4) соответственно.
Определенность при решении задач гидравлического расчета трубопроводов достигается при следующих условиях:
1. Задается расход воды.
2. Принимаются оптимальные скорости движения воды.
Наряду с общей задачей гидравлического расчета трубопроводов решаются следующие частные задачи:
1. Проверяется пропускная способность трубопровода при заданных значениях диаметров труб и напора.
2. Определяется напор при заданных значениях диаметров труб и расхода воды.
Рассмотрим определение напора по схеме, представленной на рис. 6.1.

Рис. 6.1
Применяя уравнение Бернулли, для сечений 1–1 и 2–2 запишем:
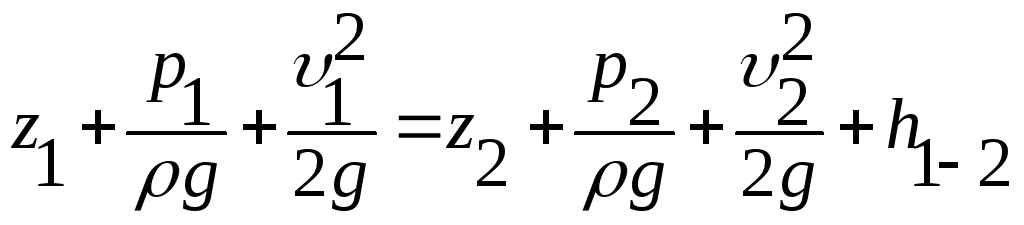 , (6.15)
, (6.15)
где | 0; |
| z; |
| |
Тогда уравнение (6.15) примет вид
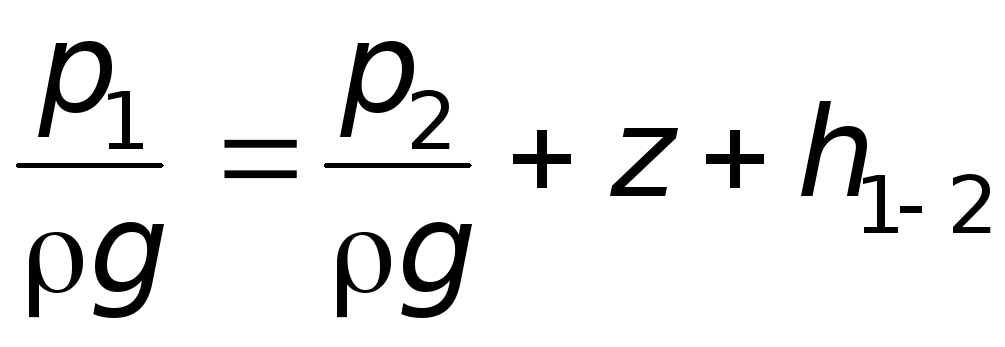 , (6.16)
, (6.16)
где | величина пьезометрического напора в сечении 1–1.Он расходуется на подъем воды на высоту z и на преодоление гидравлических сопротивлений в трубопроводеh1-2; |
| свободный напор, необходимый для преодоления местного сопротивления клапана 1 и создания скорости излива воды в бак. |
Свободный напор в местах водоразбора принимается в пределах 1…4 м и обозначается Нсв.
Тогда уравнение Бернулли (6.16) можно записать так:
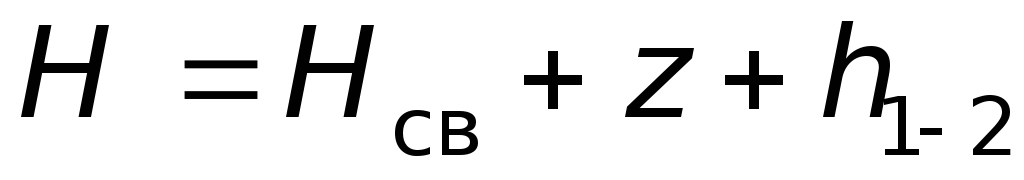 . (6.17)
. (6.17)
Для определения напора в любом сечении трубопровода необходимо знать:
– разность геометрических отметок zмежду наиболее высоко расположенным водоразбором и данным сечением потока; если точка потребления расположена ниже заданного сечения, тоzпринимается со знаком минус;
– величину свободного напора Нсвв высшей точке водоразбора;
– величину потерь напора на гидравлических сопротивлениях по пути движения воды от заданного сечения до наиболее удаленной точки водоразбора.
Так как разность отметок zи свободный напор обычно задаются, то для определения требуемого напора производится расчет потерь напора, связанных с гидравлическим сопротивлением трубопровода.
3. Напор задан. Определяются диаметры труб таким образом, чтобы выполнялось условие:
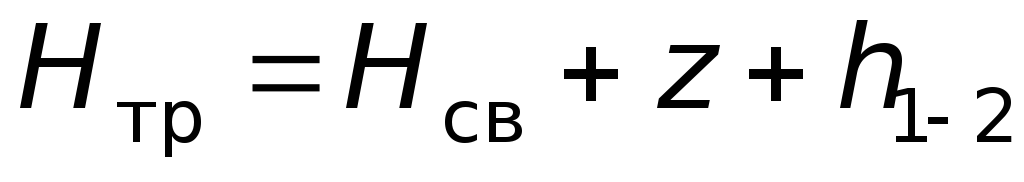 . (6.18)
. (6.18)
17 Гидравлическое сопротивление трубопроводов. Основные зависимости и принципы расчетов
Гидравлический расчет простого трубопровода производится с помощью уравнения Бернулли:
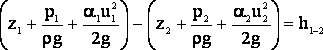
Здесь h1-2 – потери напора (энергии) на преодоление всех видов гидравлического сопротивления, приходящиеся на единицу веса движущейся жидкости.
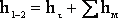
ht – потери напора на трение по длине потока,
Σhм – суммарные потери напора на местном сопротивлении Потери напора на трение по длине потока определяются по формуле Дарси-Вейсбаха
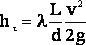
где L –длина трубопровода,
d -диаметр участка трубопровода,
v — средняя скорость течения жидкости,
λ -коэффициент гидравлического сопротивления, в общем случае зависящий от числа Рейнольдса (Re=v*d/ν), и относительной эквивалентной шероховатости труб (Δ/d).
Значения эквивалентной шероховатости Δ внутренней поверхности различных труб представлены в таблице 2. А зависимости коэффициента гидравлического сопротивления λ от числа Re и относительной шероховатости Δ/d приведены в таблице 3.
Если режим движения ламинарный, то для труб некруглого сечения коэффициент гидравлического сопротивления λ определяется по частным для каждого случая формулам (табл. 4).
При развитом турбулентном течении с достаточной степенью точности при определении λ можно пользоваться формулами для круглой трубы с заменой диаметра d на 4 гидравлических радиуса потока Rг (d=4Rг)
Rг =w/c,
где w– площадь «живого» сечения потока,
c- «смоченный» его периметр (периметр «живого» сечения по контакту жидкость – твердое тело)
Потери напора в местных сопротивлениях определяются по формуле Вейсбаха
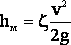
Где ς– коэффициент местного сопротивления, зависящий от конфигурации местного сопротивления и числа Рейнольдса.
При развитом турбулентном режиме ς= const, что позволяет ввести в расчеты понятие эквивалентной длины местного сопротивления Lэкв, т.е. такой длины прямого трубопровода, для которого ht= hм. В этом случае потери напора в местных сопротивлениях учитываются тем, что к реальной длине трубопровода прибавляется сумма их эквивалентных длин
Lпр =L + Lэкв,
где Lпр – приведенная длина трубопровода.
Зависимость потерь напора h1-2 от расхода называется характеристикой трубопровода.
Если движение жидкости в трубопроводе обеспечивается центробежным насосом, то для определения расхода в системе насос – трубопровод строится характеристика трубопровода h =h(Q) с учетом разности отметок ∆z (h1-2 + ∆z при z1< z2 и h1-2 — ∆z при z1>z2) накладывается на напорную характеристику насоса H=H(Q), которая приводится в паспортных данных насоса (см. рис.). Точка пересечения этих кривых указывает на максимально возможный расход в системе.
18 Категории трубопроводов тэс по Госгортехнадзору. Основные требования «Правил устройства и безопасной эксплуатации» по проектированию и устройству трубопроводов.
В зависимости от параметров (давления и температуры) транспортируемой среды станционные трубопроводы делятся на две основные группы – высокого и низкого давления. В целях унификации отдельных деталей и элементов станционных трубопроводов и обеспечения изготовления и поставки их специализированными заводами разработаны отраслевые стандарты на основные детали и элементы трубопроводов. Учитывая особенности условий работы и поставки трубопроводов, отраслевые стандарты выпускают отдельно для трубопроводов высокого и низкого давлений.
Все станционные трубопроводы должны отвечать требованиям соответствующих правил и норм, а также требованиям положений, технических условий, противоаварийных циркуляров и других нормативных документов. Одним из основных обязательных документов, определяющих правила проектирования станционных трубопроводов являются «Правила устройства и безопасной эксплуатации трубопроводов пара и горячей воды. ПБ 10-573-03».
Правила устанавливают требования к проектированию, конструкции, материалам, изготовлению, монтажу, ремонту и эксплуатации трубопроводов, транспортирующих водяной пар с рабочим давлением более 0,07 МПа (0,7 кгс/см2) или горячую воду с температурой свыше 115 град. С.
В соответствии с указанными правилами, трубопроводы пара и горячей воды, в зависимости от параметров транспортируемой среды, делятся на категории и группы.
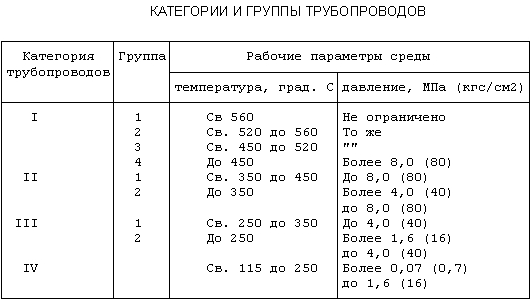
В трубопроводах должны максимально использоваться стандартизированные детали и элементы по отраслевым стандартам и ГОСТ, допустимым для условий работы станционных трубопроводов. Требования этих документов обязательно должны учитываться, начиная со стадии выполнения проектной документации. Нормативные документы, правила, ОСТ, ГОСТ подвергаются периодическим пересмотрам, исправлениям и переизданиям, поэтому при проектировании трубопроводных систем, обязательно следует пользоваться актуальными материалами на момент их применения.
Гидравлические сопротивления
4.5. Местные гидравлические сопротивления
Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов (рассмотрены в п.4.3 и 4.4) и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.
Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.
1. Внезапное расширение русла. Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.
Рис. 4.9. Внезапное расширение трубы
При внезапном расширении русла (трубы) (рис.4.9) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 — в плоскости расширения трубы и 2-2 — в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на hрасш. Эта высота и есть местная потеря напора на расширение, которая определяется по формуле:
где S1, S2 — площадь поперечных сечений 1-1 и 2-2.
Это выражение является следствием теоремы Борда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей
Выражение ( 1 — S1/S2 )2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.
Рис. 4.10. Постепенное расширение трубы
Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:
где hтр и hрасш — потери напора на трение и расширение (вихреобразование). где n = S2/S1 = ( r2/r1 ) 2 — степень расширения диффузора. Потеря напора на расширение hрасш имеет ту же самую природу, что и при внезапном расширении руслагде k — коэффициент смягчения, при α= 5…20°, k = sinα.
Учитывая это полную потерю напора можно переписать в виде:
откуда коэффициент сопротивления диффузора можно выразить формулой
Рис. 4.11. Зависимость ζдиф от угла
Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:
При подстановке в эту формулу λТ =0,015…0,025 и n = 2…4 получим αопт = 6 (рис.4.11).
3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).
Коэффициенты местного сопротивления, таблицы коэффициентов гидравлического сопротивления
Таблица коэффициентов местного сопротивления
В таблице представлены значения и расчет следующих коэффициентов местного сопротивления (или гидравлического сопротивления): местное сопротивление при входе в отверстие с острыми краями, выход из канала, коэффициент местного сопротивления трубопровода при плавном повороте на 90, от 30 до 180 градусов круглых и квадратных каналов, резкий поворот прямоугольного канала без закруглений, внезапное сужение канала, коэффициент сопротивления при внезапном расширении канала, местное сопротивление частично открытого шибера или заслонки.
Коэффициенты местного сопротивления участков
Приведены значения коэффициентов местных сопротивлений следующих участков: дроссельная заслонка, острая диафрагма, коэффициент местного сопротивления при входе в систему каналов с квадратным, круглым и прямоугольным сечением, сопротивление клапана, клапан переводной, ниша в канале, колено круглого сечения (плавный поворот на 90 градусов), коэффициент сопротивления тройника — крестовина (слияние потоков).
Таблица коэффициентов местного сопротивления воздуховодов
В таблице даны коэффициенты местного сопротивления воздуховодов при слиянии двух струй под углом 180 и поворотом на 90 градусов, сопротивление тройника раздающего, тройника собирающего и регенеративной насадки.
Гидравлические потери — Википедия
Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения[1][2]. Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах участка течения может быть и отрицательной (например, при эжекционном эффекте).
Гидравлические потери принято разделять на два вида:
- местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Гидравлические потери выражают либо в потерях напора Δh{\displaystyle \Delta h} в линейных единицах столба среды, либо в единицах давления ΔP{\displaystyle \Delta P}: Δh=ΔPρg{\displaystyle \Delta h={\Delta P \over \rho g}}, где ρ{\displaystyle \rho } — плотность среды, g — ускорение свободного падения.
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости[3] через элемент гидравлической системы пропорциональны квадрату скорости жидкости[2]. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ[4], которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что
- Δp=ζρw22, Δh=ζw22g.{\displaystyle \Delta p=\zeta {\rho w^{2} \over 2}{\mbox{, }}\Delta h=\zeta {w^{2} \over 2g}{\mbox{.}}}
То есть в предположении, что скорость w по всему сечению потока одинакова, ζ=Δp/eторм, где eторм = ρw²/2 — энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w=Q/F, где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость[1]. Таким образом, средняя энергия торможения потока обычно несколько больше ρw²/2, см. Среднее квадратическое.
Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) λ, фигурирующего в формуле Дарси — Вейсбаха[2]
- Δh=λLd⋅w22g{\displaystyle \Delta h=\lambda {\frac {L}{d}}\cdot {w^{2} \over 2g}},
где L — длина элемента, d — характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления
- Δp=λLd⋅ρw22{\displaystyle \Delta p=\lambda {\frac {L}{d}}\cdot {\rho w^{2} \over 2}};
таким образом, для линейного элемента относительной длины L/d коэффициент сопротивления трения ζтр=λL/d.
Влияние режима течения в трубах на гидравлические потери[править | править код]
Поскольку при турбулентном режиме течения происходит расход энергии потока на преодоление вязкости при турбулентных колебаниях, гидравлические потери при ламинарном режиме течения жидкости значительно меньше, чем при турбулентном. Так, например, если бы в системах водоснабжения и отопления при существующих скоростях движения жидкостей возможно было бы поддерживать ламинарный режим течения, то напор насосов можно было бы уменьшить в 5—10 раз[источник не указан 2770 дней]. Изменение режима течения с ламинарного на турбулентный вызывает скачкообразное увеличение сопротивления (при некоторых скоростях, т.е. в некотором диапазоне чисел Рейнольдса, ламинарное течение неустойчиво, но в определённых условиях может существовать). В то же время коэффициент гидравлического сопротивления при ламинарном режиме обычно получается больше, чем при турбулентном, поскольку для ламинарных режимов характерны более низкие скорости. При ламинарном режиме сопротивление примерно линейно зависит от скорости (соответственно, коэффициент примерно линейно падает, например, в круглых трубах λ=64Re{\displaystyle \lambda ={\frac {64}{\mathrm {Re} }}}). При турбулентном режиме в гидравлически гладких трубах (при небольших шероховатостях и небольших Re) зависимость имеет иной характер (для круглых труб λ=0,3164Re4.{\displaystyle \lambda ={\frac {0,3164}{\sqrt[{4}]{\mathrm {Re} }}}.}) и во всех практически реализуемых случаях лежит выше зависимости для ламинарного режима; при бо́льших числах Рейнольдса под влиянием шероховатости график λ претерпевает сложный изгиб, и начиная с некоторого критического значения при Re>Reкр (область автомодельности) λ зависит только от шероховатости.
На преодоление гидравлических потерь в различных технических системах затрачивается работа таких устройств, как насосы, воздуходувки.
Для уменьшения гидравлических потерь рекомендуется в конструкциях гидрооборудования избегать применения деталей, способствующих резкому изменению направления потока — например, заменять внезапное расширение трубы постепенным расширением (диффузор), придавать телам, движущимся в жидкостях, обтекаемую форму и др. Даже в абсолютно гладких трубах имеются гидравлические потери[2]; при ламинарном режиме шероховатость мало на них влияет, однако при обычных в технике турбулентных режимах её увеличение, как правило, вызывает рост гидродинамического сопротивления.
Иногда, напротив, требуется ввести гидравлическое сопротивление в поток. Для этого применяются дроссельные шайбы, редукционные установки, регулирующие клапаны. По измерению давления на некотором элементе, график коэффициента гидравлического сопротивления которого известен, можно узнать скорость потока в некоторых распространённых типах расходомеров.
- ↑ 1 2 Идельчик И. Е. Справочник по гидравлическим сопротивлениям/ Под ред. М. О. Штейнберга. — 3-е изд., перераб. и доп.— М.: Машиностроение, 1992. — C. 10
- ↑ 1 2 3 4 Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов / Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др.. — 2-е изд., перераб.. — М.: Машиностроение, 1982. — С. 48—50, 84, 88.
- ↑ В гидродинамике жидкостью называется любая текучая среда, как капельная жидкость, так и газ.
- ↑ Также применяется обозначение ξ; буквы часто путают, иногда применяют для различения того, во входном или выходном сечении элемента измерялась скорость в формуле (для расширяющихся или сужающихся элементов).

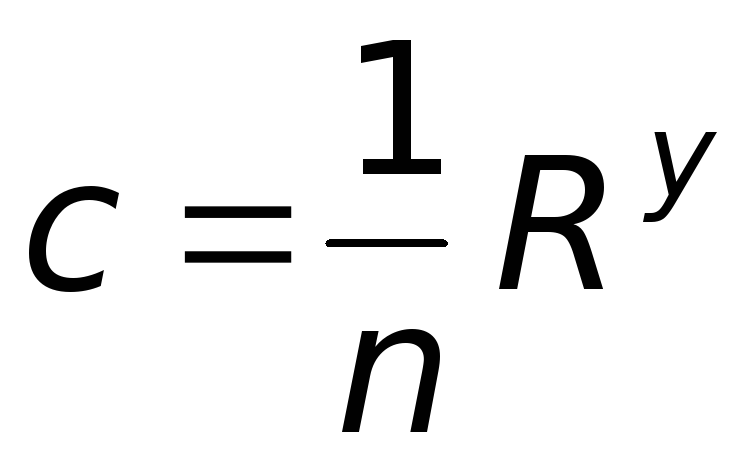 –
–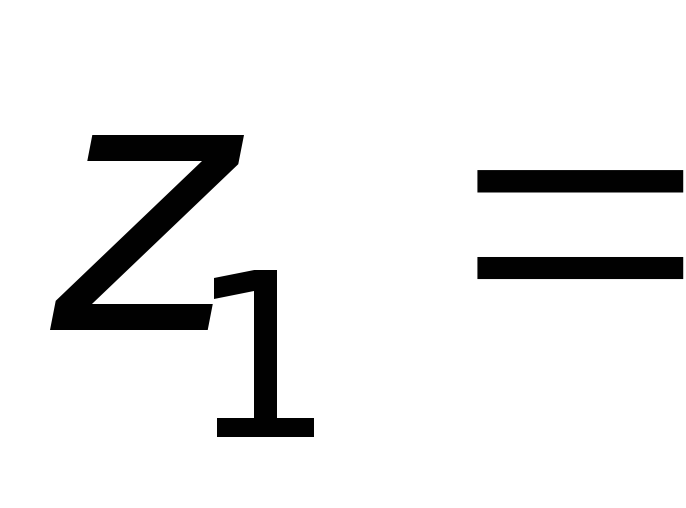
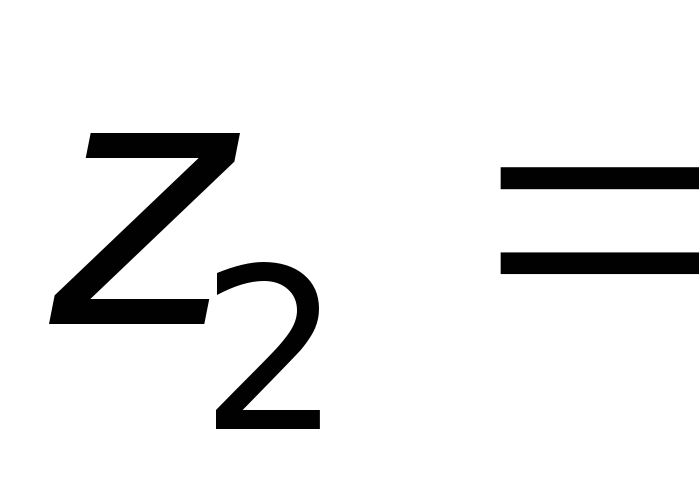
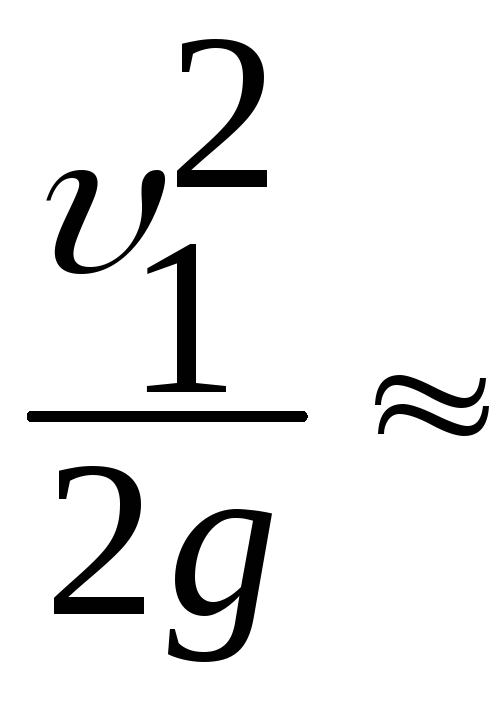
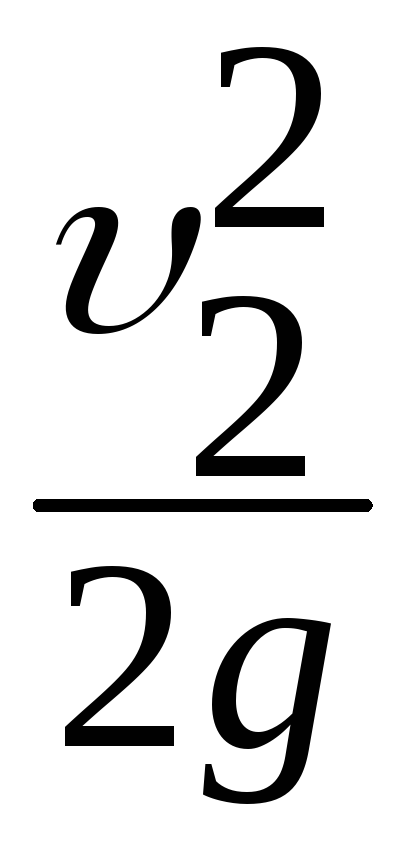 ,
так как величина скоростных напоров
городского водопровода мала и ею можно
пренебречь (v1v2)
(на практике эта разность – около 5
см).
,
так как величина скоростных напоров
городского водопровода мала и ею можно
пренебречь (v1v2)
(на практике эта разность – около 5
см).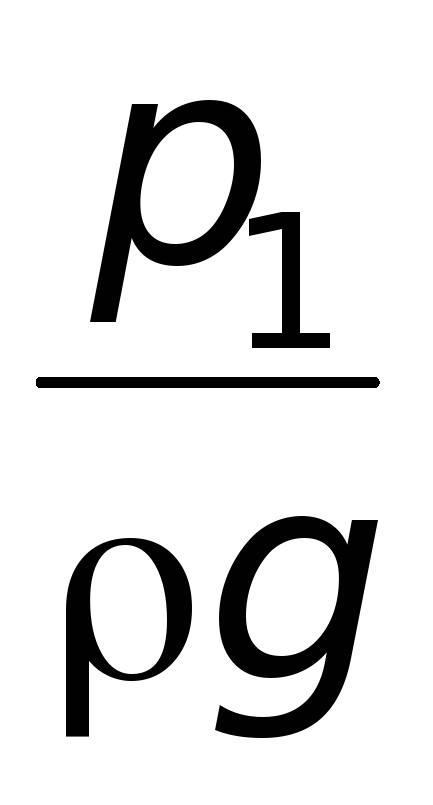 –
–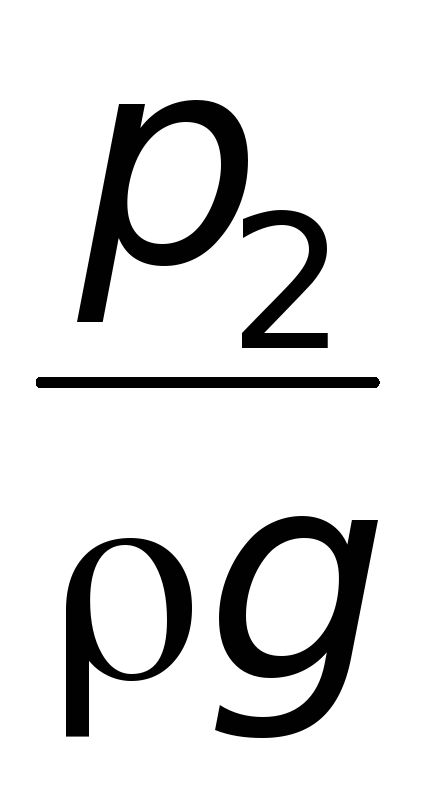 –
–