Расчетные значения для прямоугольных профильных труб
Таблица 1.1. Прямоугольные профильные трубы высотой 50-80 мм
Таблица 1.2. Прямоугольные профильные трубы высотой 80-100 мм
Таблица 1.3. Прямоугольные профильные трубы высотой 120-150 мм
Таблица 1.4. Прямоугольные профильные трубы высотой 160-180 мм
Таблица 1.5. Прямоугольные профильные трубы высотой 180-220 мм
Таблица 1.6. Прямоугольные профильные трубы высотой 220-300 мм
Таблица 1.7. Прямоугольные профильные трубы высотой 300-400 мм
Примечания:
1. Условные обозначения: h — высота профиля; b — ширина профиля; F — площадь поперечного сечения; R — радиус наружного закругления угла; I — момент инерции; W — момент сопротивления; i — радиус инерции.
2. Радиус наружного закругления угла R = 2,0t при t ≤ 6,0 мм; R = 2,5t при 6,0 < t ≤ 10,0 мм; R = 3,0t при t > 10,0 мм.
3. Масса 1 м длины профиля определена по площади поперечного сечения, при плотности стали 7,85 г/см3.
Основные геометрические характеристики сечений для прямоугольных профильных труб малого сечения приводятся отдельно.
Калькулятор расчета характеристик кольцевого сечения (трубы)
- Подробности
Калькулятор онлайн рассчитывает
| Исходные данные: | ||
| Наружный диаметр d, мм |
 |
|
| Толщина стенки s, мм | ||
| Определение вспомогательных данных: | ||
| Внутренний диаметр d1, мм | расчет внутреннего диаметра кольца | |
| Решение: | ||
| Площадь сечения, мм2 | расчет площади сечения кольца | |
| Осевые моменты инерции относительно центральных осей, мм4 |
расчет момента инерции кольца относительно оси ОХ расчет момента инерции кольца относительно оси ОY |
|
|
расчет момента сопротивления изгибу кольца относительно оси ОХ расчет момента сопротивления изгибу кольца относительно оси ОY |
||
| Радиусы инерции сечения, мм |
расчет радиуса инерции кольца относительно оси ОХ расчет радиуса инерции кольца относительно оси ОY |
|
Помощь на развитие проекта CAE-CUBE.ru
Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали — обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Спасибо, что не прошели мимо!
I. Порядок действий при расчете характеристик кольцевого сечения (трубы):
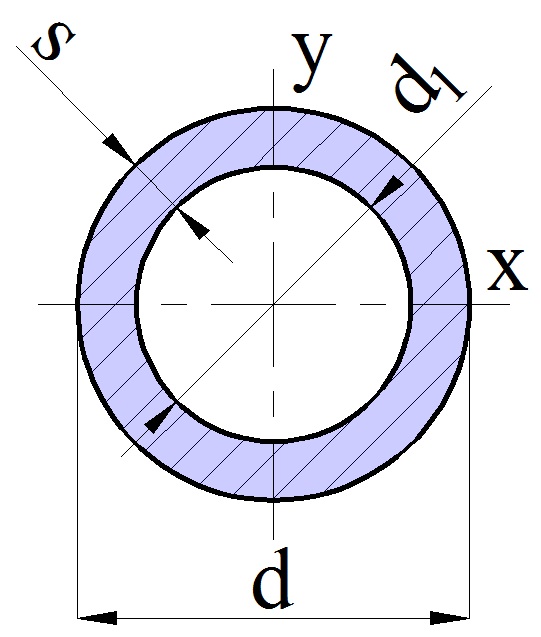
- Для проведения расчета требуется ввести наружный диаметр сечения d и толщину стенки s.
- По введенным данным программа автоматически вычисляет внутренний диаметр сечения d1.
- Результаты расчета площади, моментов сопротивления изгибу, моментов и радиусов инерции кольцевого сечения выводятся автоматически.
- На рисунке справа приведены необходимые размеры элементов сечения.
II. Примечание:
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
Сортамент гнутых замкнутых сварных профилей квадратного сечения по ГОСТ 30245-2003 (квадратные трубы)
Сортамент гнутых замкнутых сварных профилей квадратного сечения по ГОСТ 30245-2003 (квадратные трубы)Сортамент гнутых замкнутых сварных профилей квадратного
сечения по ГОСТ 30245-2003 (квадратные трубы)
(с исправлениями)
Вернуться к списку сортаментов
Условные обозначения:
b - высота/ширина профиля;
s - толщина профиля;
R - радиус наружного закругления;
I - момент инерции;
W - момент сопротивления;
i - радиус инерции;
Примечание:
R=2,0*s при s10,0 мм
|
Сортамент гнутых замкнутых сварных профилей квадратного сечения
по ГОСТ 30245-2003 (квадратные трубы)
Геометрические характеристики вычислены по программе КМБП
(http://hdru.com/russian/kmbp_2/rec_2_02.htm)
╔═══════╤════════╤═════════════╤═════════════════════════════╤══════════╗
║ b │ s │ Площадь │Справочные значения для осей │ Масса 1м ║
║ │ │ поперечного ├─────────────────────────────┤ длины ║
║ │ │ сечения │ X - X и Y - Y │ ║
╟───────┴────────┤ ├─────────┬─────────┬─────────┤ ║
║ │ │ Jx=Jy │ Wx=Wy │ ix=iy │ ║
║ мм │ (см2) │ (см4) │ (см3) │ (см) │ (кг) ║
╠═══════╤════════╪═════════════╪═════════╪═════════╪═════════╪══════════╣
║ 40 │ 2.0 │ 2.94 │ 6.94│ 3.47 │ 1.54 │ 2.31 ║
║ │ 2.5 │ 3.59 │ 8.21│ 4.11 │ 1.51 │ 2.82 ║
║ │ 3.0 │ 4.21 │ 9.32│ 4.66 │ 1.49 │ 3.30 ║
║ │ 3.5 │ 4.79 │ 10.27│ 5.14 │ 1.46 │ 3.76 ║
║ │ 4.0 │ 5.35 │ 11.07│ 5.54 │ 1.44 │ 4.20 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 50 │ 2.0 │ 3.74 │ 14.15│ 5.66 │ 1.95 │ 2.93 ║
║ │ 2.5 │ 4.59 │ 16.94│ 6.78 │ 1.92 │ 3.60 ║
║ │ 3.0 │ 5.41 │ 19.47│ 7.79 │ 1.90 │ 4.25 ║
║ │ 3.5 │ 6.20 │ 21.73│ 8.69 │ 1.87 │ 4.86 ║
║ │ 4.0 │ 6.95 │ 23.74│ 9.49 │ 1.85 │ 5.45 ║
║ │ 4.5 │ 7.67 │ 25.50│ 10.20 │ 1.82 │ 6.02 ║
║ │ 5.0 │ 8.36 │ 27.04│ 10.82 │ 1.80 │ 6.56 ║
║ │ 5.5 │ 9.01 │ 28.35│ 11.34 │ 1.77 │ 7.07 ║
║ │ 6.0 │ 9.63 │ 29.45│ 11.78 │ 1.75 │ 7.56 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 60 │ 2.0 │ 4.54 │ 25.14│ 8.38 │ 2.35 │ 3.56 ║
║ │ 2.5 │ 5.59 │ 30.34│ 10.11 │ 2.33 │ 4.39 ║
║ │ 3.0 │ 6.61 │ 35.13│ 11.71 │ 2.31 │ 5.19 ║
║ │ 3.5 │ 7.59 │ 39.53│ 13.18 │ 2.28 │ 5.96 ║
║ │ 4.0 │ 8.55 │ 43.55│ 14.52 │ 2.26 │ 6.71 ║
║ │ 4.5 │ 9.47 │ 47.20│ 15.73 │ 2.23 │ 7.43 ║
║ │ 5.0 │ 10.36 │ 50.49│ 16.83 │ 2.21 │ 8.13 ║
║ │ 5.5 │ 11.21 │ 53.45│ 17.82 │ 2.18 │ 8.80 ║
║ │ 6.0 │ 12.03 │ 56.07│ 18.69 │ 2.16 │ 9.45 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 70 │ 2.0 │ 5.34 │ 40.73│ 11.64 │ 2.76 │ 4.19 ║
║ │ 2.5 │ 6.59 │ 49.41│ 14.12 │ 2.74 │ 5.17 ║
║ │ 3.0 │ 7.81 │ 57.53│ 16.44 │ 2.71 │ 6.13 ║
║ │ 3.5 │ 8.99 │ 65.09│ 18.60 │ 2.69 │ 7.06 ║
║ │ 4.0 │ 10.15 │ 72.12│ 20.61 │ 2.67 │ 7.97 ║
║ │ 4.5 │ 11.27 │ 78.63│ 22.47 │ 2.64 │ 8.85 ║
║ │ 5.0 │ 12.36 │ 84.63│ 24.18 │ 2.62 │ 9.70 ║
║ │ 5.5 │ 13.41 │ 90.14│ 25.75 │ 2.59 │ 10.53 ║
║ │ 6.0 │ 14.43 │ 95.17│ 27.19 │ 2.57 │ 11.33 ║
║ │ 6.5 │ 15.06 │ 95.28│ 27.22 │ 2.52 │ 11.82 ║
║ │ 7.0 │ 15.96 │ 98.70│ 28.20 │ 2.49 │ 12.53 ║
╚═══════╧════════╧═════════════╧═════════╧═════════╧═════════╧══════════╝
Сортамент гнутых замкнутых сварных профилей квадратного сечения
по ГОСТ 30245-2003 (квадратные трубы)
╔═══════╤════════╤═════════════╤═════════════════════════════╤══════════╗
║ b │ s │ Площадь │Справочные значения для осей │ Масса 1м ║
║ │ │ поперечного ├─────────────────────────────┤ длины ║
║ │ │ сечения │ X - X и Y - Y │ ║
╟───────┴────────┤ ├─────────┬─────────┬─────────┤ ║
║ │ │ Jx=Jy │ Wx=Wy │ ix=iy │ ║
║ мм │ (см2) │ (см4) │ (см3) │ (см) │ (кг) ║
╠═══════╤════════╪═════════════╪═════════╪═════════╪═════════╪══════════╣
║ 80 │ 3.0 │ 9.01 │ 87.84│ 21.96 │ 3.12 │ 7.07 ║
║ │ 3.5 │ 10.39 │ 99.80│ 24.95 │ 3.10 │ 8.16 ║
║ │ 4.0 │ 11.75 │ 111.04│ 27.76 │ 3.07 │ 9.22 ║
║ │ 4.5 │ 13.07 │ 121.58│ 30.40 │ 3.05 │ 10.26 ║
║ │ 5.0 │ 14.36 │ 131.44│ 32.86 │ 3.03 │ 11.27 ║
║ │ 5.5 │ 15.61 │ 140.63│ 35.16 │ 3.00 │ 12.25 ║
║ │ 6.0 │ 16.83 │ 149.18│ 37.29 │ 2.98 │ 13.21 ║
║ │ 6.5 │ 17.66 │ 151.25│ 37.81 │ 2.93 │ 13.86 ║
║ │ 7.0 │ 18.76 │ 157.61│ 39.40 │ 2.90 │ 14.72 ║
║ │ 7.5 │ 19.82 │ 163.32│ 40.83 │ 2.87 │ 15.56 ║
║ │ 8.0 │ 20.84 │ 168.38│ 42.09 │ 2.84 │ 16.36 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 90 │ 3.0 │ 10.21 │ 127.28│ 28.29 │ 3.53 │ 8.01 ║
║ │ 3.5 │ 11.79 │ 145.06│ 32.24 │ 3.51 │ 9.26 ║
║ │ 4.0 │ 13.35 │ 161.92│ 35.98 │ 3.48 │ 10.48 ║
║ │ 4.5 │ 14.87 │ 177.87│ 39.53 │ 3.46 │ 11.67 ║
║ │ 5.0 │ 16.36 │ 192.93│ 42.87 │ 3.43 │ 12.84 ║
║ │ 5.5 │ 17.81 │ 207.13│ 46.03 │ 3.41 │ 13.98 ║
║ │ 6.0 │ 19.23 │ 220.48│ 48.99 │ 3.39 │ 15.10 ║
║ │ 6.5 │ 20.26 │ 225.60│ 50.13 │ 3.34 │ 15.90 ║
║ │ 7.0 │ 21.56 │ 236.13│ 52.47 │ 3.31 │ 16.92 ║
║ │ 7.5 │ 22.82 │ 245.79│ 54.62 │ 3.28 │ 17.91 ║
║ │ 8.0 │ 24.04 │ 254.59│ 56.58 │ 3.25 │ 18.87 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 100 │ 3.0 │ 11.41 │ 177.05│ 35.41 │ 3.94 │ 8.96 ║
║ │ 3.5 │ 13.19 │ 202.28│ 40.46 │ 3.92 │ 10.36 ║
║ │ 4.0 │ 14.95 │ 226.35│ 45.27 │ 3.89 │ 11.73 ║
║ │ 4.5 │ 16.67 │ 249.29│ 49.86 │ 3.87 │ 13.08 ║
║ │ 5.0 │ 18.36 │ 271.10│ 54.22 │ 3.84 │ 14.41 ║
║ │ 5.5 │ 20.01 │ 291.82│ 58.36 │ 3.82 │ 15.71 ║
║ │ 6.0 │ 21.63 │ 311.47│ 62.29 │ 3.79 │ 16.98 ║
║ │ 6.5 │ 22.86 │ 320.93│ 64.19 │ 3.75 │ 17.94 ║
║ │ 7.0 │ 24.36 │ 337.04│ 67.41 │ 3.72 │ 19.12 ║
║ │ 7.5 │ 25.82 │ 352.04│ 70.41 │ 3.69 │ 20.27 ║
║ │ 8.0 │ 27.24 │ 365.94│ 73.19 │ 3.67 │ 21.39 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 120 │ 3.0 │ 13.81 │ 312.35│ 52.06 │ 4.76 │ 10.84 ║
║ │ 3.5 │ 15.99 │ 358.17│ 59.69 │ 4.73 │ 12.56 ║
║ │ 4.0 │ 18.15 │ 402.28│ 67.05 │ 4.71 │ 14.25 ║
║ │ 4.5 │ 20.27 │ 444.70│ 74.12 │ 4.68 │ 15.91 ║
║ │ 5.0 │ 22.36 │ 485.47│ 80.91 │ 4.66 │ 17.55 ║
║ │ 5.5 │ 24.41 │ 524.62│ 87.44 │ 4.64 │ 19.16 ║
║ │ 6.0 │ 26.43 │ 562.16│ 93.69 │ 4.61 │ 20.75 ║
║ │ 6.5 │ 28.06 │ 584.95│ 97.49 │ 4.57 │ 22.03 ║
║ │ 7.0 │ 29.96 │ 617.26│ 102.88 │ 4.54 │ 23.52 ║
║ │ 7.5 │ 31.82 │ 647.90│ 107.98 │ 4.51 │ 24.98 ║
║ │ 8.0 │ 33.64 │ 676.88│ 112.81 │ 4.49 │ 26.41 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 140 │ 4.0 │ 21.35 │ 651.62│ 93.09 │ 5.53 │ 16.76 ║
║ │ 4.5 │ 23.87 │ 722.24│ 103.18 │ 5.50 │ 18.74 ║
║ │ 5.0 │ 26.36 │ 790.56│ 112.94 │ 5.48 │ 20.69 ║
║ │ 5.5 │ 28.81 │ 856.61│ 122.37 │ 5.45 │ 22.62 ║
║ │ 6.0 │ 31.23 │ 920.43│ 131.49 │ 5.43 │ 24.52 ║
╚═══════╧════════╧═════════════╧═════════╧═════════╧═════════╧══════════╝
Сортамент гнутых замкнутых сварных профилей квадратного сечения
по ГОСТ 30245-2003 (квадратные трубы)
╔═══════╤════════╤═════════════╤═════════════════════════════╤══════════╗
║ b │ s │ Площадь │Справочные значения для осей │ Масса 1м ║
║ │ │ поперечного ├─────────────────────────────┤ длины ║
║ │ │ сечения │ X - X и Y - Y │ ║
╟───────┴────────┤ ├─────────┬─────────┬─────────┤ ║
║ │ │ Jx=Jy │ Wx=Wy │ ix=iy │ ║
║ мм │ (см2) │ (см4) │ (см3) │ (см) │ (кг) ║
╠═══════╤════════╪═════════════╪═════════╪═════════╪═════════╪══════════╣
║ 140 │ 6.5 │ 33.26 │ 964.11│ 137.73 │ 5.38 │ 26.11 ║
║ │ 7.0 │ 35.56 │ 1020.70│ 145.81 │ 5.36 │ 27.91 ║
║ │ 7.5 │ 37.82 │ 1074.90│ 153.56 │ 5.33 │ 29.69 ║
║ │ 8.0 │ 40.04 │ 1126.80│ 160.97 │ 5.30 │ 31.43 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 150 │ 4.0 │ 22.95 │ 807.82│ 107.71 │ 5.93 │ 18.01 ║
║ │ 4.5 │ 25.67 │ 896.30│ 119.51 │ 5.91 │ 20.15 ║
║ │ 5.0 │ 28.36 │ 982.12│ 130.95 │ 5.88 │ 22.26 ║
║ │ 5.5 │ 31.01 │ 1065.30│ 142.04 │ 5.86 │ 24.34 ║
║ │ 6.0 │ 33.63 │ 1145.90│ 152.79 │ 5.84 │ 26.40 ║
║ │ 6.5 │ 35.86 │ 1203.40│ 160.45 │ 5.79 │ 28.15 ║
║ │ 7.0 │ 38.36 │ 1275.60│ 170.08 │ 5.77 │ 30.11 ║
║ │ 7.5 │ 40.82 │ 1345.10│ 179.34 │ 5.74 │ 32.04 ║
║ │ 8.0 │ 43.24 │ 1411.80│ 188.24 │ 5.71 │ 33.95 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 160 │ 4.0 │ 24.55 │ 987.17│ 123.40 │ 6.34 │ 19.27 ║
║ │ 4.5 │ 27.47 │ 1096.30│ 137.04 │ 6.32 │ 21.56 ║
║ │ 5.0 │ 30.36 │ 1202.40│ 150.29 │ 6.29 │ 23.83 ║
║ │ 5.5 │ 33.21 │ 1305.40│ 163.18 │ 6.27 │ 26.07 ║
║ │ 6.0 │ 36.03 │ 1405.50│ 175.69 │ 6.25 │ 28.29 ║
║ │ 6.5 │ 38.46 │ 1479.20│ 184.90 │ 6.20 │ 30.19 ║
║ │ 7.0 │ 41.16 │ 1569.70│ 196.21 │ 6.18 │ 32.31 ║
║ │ 7.5 │ 43.82 │ 1657.00│ 207.13 │ 6.15 │ 34.40 ║
║ │ 8.0 │ 46.44 │ 1741.20│ 217.65 │ 6.12 │ 36.46 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 180 │ 5.0 │ 34.36 │ 1736.90│ 192.99 │ 7.11 │ 26.97 ║
║ │ 5.5 │ 37.61 │ 1888.60│ 209.85 │ 7.09 │ 29.52 ║
║ │ 6.0 │ 40.83 │ 2036.50│ 226.28 │ 7.06 │ 32.05 ║
║ │ 6.5 │ 43.66 │ 2151.10│ 239.01 │ 7.02 │ 34.27 ║
║ │ 7.0 │ 46.76 │ 2286.70│ 254.08 │ 6.99 │ 36.70 ║
║ │ 7.5 │ 49.82 │ 2418.30│ 268.70 │ 6.97 │ 39.11 ║
║ │ 8.0 │ 52.84 │ 2545.90│ 282.87 │ 6.94 │ 41.48 ║
║ │ 8.5 │ 55.83 │ 2669.50│ 296.61 │ 6.92 │ 43.83 ║
║ │ 9.0 │ 58.78 │ 2789.10│ 309.90 │ 6.89 │ 46.14 ║
║ │ 9.5 │ 61.69 │ 2904.90│ 322.77 │ 6.86 │ 48.43 ║
║ │ 10.0 │ 64.57 │ 3016.80│ 335.20 │ 6.83 │ 50.68 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 200 │ 6.0 │ 45.63 │ 2832.70│ 283.27 │ 7.88 │ 35.82 ║
║ │ 6.5 │ 48.86 │ 3000.40│ 300.04 │ 7.84 │ 38.35 ║
║ │ 7.0 │ 52.36 │ 3194.10│ 319.41 │ 7.81 │ 41.10 ║
║ │ 7.5 │ 55.82 │ 3382.70│ 338.27 │ 7.79 │ 43.82 ║
║ │ 8.0 │ 59.24 │ 3566.30│ 356.63 │ 7.76 │ 46.51 ║
║ │ 8.5 │ 62.63 │ 3744.80│ 374.48 │ 7.73 │ 49.16 ║
║ │ 9.0 │ 65.98 │ 3918.50│ 391.85 │ 7.71 │ 51.79 ║
║ │ 9.5 │ 69.29 │ 4087.20│ 408.72 │ 7.68 │ 54.39 ║
║ │ 10.0 │ 72.57 │ 4251.10│ 425.11 │ 7.65 │ 56.96 ║
║ │ 10.5 │ 74.86 │ 4311.90│ 431.19 │ 7.59 │ 58.76 ║
║ │ 11.0 │ 77.97 │ 4456.50│ 445.65 │ 7.56 │ 61.20 ║
║ │ 11.5 │ 81.03 │ 4595.90│ 459.59 │ 7.53 │ 63.61 ║
║ │ 12.0 │ 84.06 │ 4730.20│ 473.02 │ 7.50 │ 65.99 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 250 │ 6.0 │ 57.63 │ 5672.00│ 453.76 │ 9.92 │ 45.24 ║
║ │ 6.5 │ 61.86 │ 6037.10│ 482.97 │ 9.88 │ 48.56 ║
╚═══════╧════════╧═════════════╧═════════╧═════════╧═════════╧══════════╝
Сортамент гнутых замкнутых сварных профилей квадратного сечения
по ГОСТ 30245-2003 (квадратные трубы)
╔═══════╤════════╤═════════════╤═════════════════════════════╤══════════╗
║ b │ s │ Площадь │Справочные значения для осей │ Масса 1м ║
║ │ │ поперечного ├─────────────────────────────┤ длины ║
║ │ │ сечения │ X - X и Y - Y │ ║
╟───────┴────────┤ ├─────────┬─────────┬─────────┤ ║
║ │ │ Jx=Jy │ Wx=Wy │ ix=iy │ ║
║ мм │ (см2) │ (см4) │ (см3) │ (см) │ (кг) ║
╠═══════╤════════╪═════════════╪═════════╪═════════╪═════════╪══════════╣
║ 250 │ 7.0 │ 66.36 │ 6442.60│ 515.41 │ 9.85 │ 52.09 ║
║ │ 7.5 │ 70.82 │ 6839.90│ 547.19 │ 9.83 │ 55.59 ║
║ │ 8.0 │ 75.24 │ 7229.20│ 578.34 │ 9.80 │ 59.07 ║
║ │ 8.5 │ 79.63 │ 7610.50│ 608.84 │ 9.78 │ 62.51 ║
║ │ 9.0 │ 83.98 │ 7983.80│ 638.70 │ 9.75 │ 65.92 ║
║ │ 9.5 │ 88.29 │ 8349.10│ 667.93 │ 9.72 │ 69.31 ║
║ │ 10.0 │ 92.57 │ 8706.70│ 696.53 │ 9.70 │ 72.66 ║
║ │ 10.5 │ 95.86 │ 8903.80│ 712.30 │ 9.64 │ 75.25 ║
║ │ 11.0 │ 99.97 │ 9230.70│ 738.46 │ 9.61 │ 78.47 ║
║ │ 11.5 │ 104.03 │ 9549.20│ 763.94 │ 9.58 │ 81.67 ║
║ │ 12.0 │ 108.06 │ 9859.40│ 788.75 │ 9.55 │ 84.83 ║
╟───────┼────────┼─────────────┼─────────┼─────────┼─────────┼──────────╢
║ 300 │ 6.0 │ 69.63 │ 9963.70│ 664.24 │ 11.96 │ 54.66 ║
║ │ 6.5 │ 74.86 │ 10638.00│ 709.23 │ 11.92 │ 58.76 ║
║ │ 7.0 │ 80.36 │ 11371.00│ 758.07 │ 11.90 │ 63.08 ║
║ │ 7.5 │ 85.82 │ 12092.00│ 806.12 │ 11.87 │ 67.37 ║
║ │ 8.0 │ 91.24 │ 12801.00│ 853.38 │ 11.84 │ 71.63 ║
║ │ 8.5 │ 96.63 │ 13498.00│ 899.86 │ 11.82 │ 75.85 ║
║ │ 9.0 │ 101.98 │ 14183.00│ 945.55 │ 11.79 │ 80.05 ║
║ │ 9.5 │ 107.29 │ 14857.00│ 990.47 │ 11.77 │ 84.22 ║
║ │ 10.0 │ 112.57 │ 15519.00│ 1034.60 │ 11.74 │ 88.36 ║
║ │ 10.5 │ 116.86 │ 15951.00│ 1063.40 │ 11.68 │ 91.73 ║
║ │ 11.0 │ 121.97 │ 16569.00│ 1104.60 │ 11.66 │ 95.74 ║
║ │ 11.5 │ 127.03 │ 17174.00│ 1145.00 │ 11.63 │ 99.72 ║
║ │ 12.0 │ 132.06 │ 17767.00│ 1184.50 │ 11.60 │ 103.67 ║
╚═══════╧════════╧═════════════╧═════════╧═════════╧═════════╧══════════╝
Момент инерции и момент сопротивления
05-12-2012: Адольф СталинБыло бы неплохо объяснить на наглядном примере для особо одаренных, типа меня, что такое момент инерции и с чем его едят. На специализированных сайтах как-то всё очень запутанно, а у Дока есть явный талант довести информацию, быть может не самую сложную, но очень грамотно и понятно
05-12-2012: Доктор Лом
В принципе, что такое момент инерции и откуда он взялся, достаточно подробно объяснено в статье «Основы сопромата, расчетные формулы», здесь лишь повторюсь: «W — это момент сопротивления поперечного сечения балки, другими словами, площадь сжимаемой или растягиваемой части сечения балки, умноженная на плечо действия равнодействующей силы». Момент сопротивления необходимо знать для расчетов конструкции на прочность, т.е. по предельным напряжениям. Момент инерции необходимо знать для определения углов поворота поперечного сечения и прогиба (смещения) центра тяжести поперечного сечения, так как максимальные деформации возникают в самом верхнем и в самом нижнем слое изгибаемой конструкции, то определить момент инерции можно, умножив момент сопротивления на расстояние от центра тяжести сечения до верхнего или нижнего слоя, поэтому для прямоугольных сечений I=Wh/2. При определении момента инерции сечений сложных геометрических форм сначала сложная фигура разбивается на простейшие, затем определяются площади сечения этих фигур и моменты инерции простейших фигур, затем площади простейших фигур умножаются на квадрат расстояния от общего центра тяжести сечения до центра тяжести простейшей фигуры. Момент инерции простейшей фигуры в составе сложного сечения равен моменту инерции фигуры + квадрат расстояния умноженный на площадь. Затем полученные моменты инерции суммируются и получается момент инерции сложного сечения. Но это максимально упрощенные формулировки (хотя, соглашусь, все равно выглядит достаточно мудрено). Со временем напишу отдельную статью.
05-12-2012: Гиви
В принципе все предельно ясно, но здесь проще www.kataltim.ru
20-04-2013: Petr
Не нужно полностью доверять поданной в сайтах информации. Её никто по-хорошему не проверяет. И ссылки на неё не даются. Так в Таблице 1. «Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций достаточно простых геометрических форм» для тонкостенной трубы дается определение, что отношение диаметра к толщине оболочки должно быть больше 10. По другим источникам — должно быть больше 20!!! (Н.М. Беляев. Сопротивление материалов. М.1996. стр.160. или Н.И.Безухов. Основы теории упругости, пластичности и ползучести.М.1961.стр.390)
21-04-2013: Доктор Лом
Верно. Доверять нельзя. Но логическое мышление пока никто не отменял. Самый правильный вариант — рассчитывать момент инерции или момент сопротивления для любой трубы по формулам, приведенным для обычной трубы (на 1 пункт выше). Формулы, приводимые для тонкостенной трубы, в любом случае будут приближенными и годятся только для первичного расчета и об этом забывать нельзя.
Впрочем параметры максимально допустимой толщины стенки исправил.
25-06-2013: Саня
требуется определить момент инерции для сложного нестандартного сечения. сечение: прямоугольник с двумя пазами. внешне похоже на букву «Ш». не получается найти какую либо информацию. буду признателен за какую нибудь информацию
25-06-2013: Доктор Лом
Посмотрите статью «Расчет прочности потолочного профиля для гипсокартона» (http://doctorlom.com/item249.html)
там в частности определяется момент инерции тоже не совсем простого сечения.
03-11-2014: Радик
Вот здесь http://otvet.mail.ru/question/33111076
дана другая формула для момента сопротивления трубы, а именно: W=(D^3-d^3)*3,14/32.
Объясните, пожалуйста, правильность этой формулы (или неправильность).
04-11-2014: Доктор Лом
Формула из приведенного вами источника неправильная (ею можно пользоваться только для приблизительных вычислений) и проверить это легко.
Чтобы определить момент инерции сечения трубы, достаточно вычесть из момента инерции стержня круглого сечения (тут при вычислениях используется наружный диаметр трубы) момент инерции отверстия (внутренний диаметр, ведь внутри трубы никакого материала нет, на то она и труба). После простейших математических преобразований мы получим формулу момента инерции трубы, приведенную в таблице.
А для того, чтобы определить момент сопротивления, нужно момент инерции разделить на максимальное расстояние от центра тяжести до самой дальней точки сечения, соответственно на D/2, или умножить на 2/D.
В итоге получить указанную вами формулу невозможно и чем толще будет стенка трубы, тем больше будет погрешность при использовании этой формулы.
04-11-2014: Радик
Спасибо, док!
11-11-2014: Ильгам
Не смог найти инфо о том в каких единицах (мм, см, м) все значения в формулах.
Попробовал посчитать Wz для уголка 210х90мм (если у швел.24П срезать верхнюю полку), получилось 667,5 см3, при условии что все значения в см.
Для примера, у швел.24П (до срезания полки) Wx(Wz)=243 см3.
11-11-2014: Доктор Лом
Это общие формулы. В каких единицах подставите значения, в таких и получите результат, только само собой уже в кубических. Но если начали подставлять, например, в сантиметрах, то так и нужно продолжать.
У швеллера без полки момент сопротивления по умолчанию не может быть больше чем у целого швеллера. Для приблизительного определения момента сопротивления швеллера без полки вы можете воспользоваться формулами для неравнополочного уголка (только для определения Wz, для Wy эти формулы не подойдут).
04-01-2015: Valerij
Если сечение трубы ослаблено несколькими значительными отверстиями, как учесть это при расчёте момента инерции и момента сопротивления? Труба 32.39см и в ней 9 отв. диам.2.8см в сечении(шаг отвермтий 10см. по длине трубы).
05-01-2015: Доктор Лом
Для определения момента инерции вам нужно вычесть из момента инерции трубы момент инерции вашего отверстия. Для этого нужно определить площадь сечения отверстия и затем умножить ее на квадрат расстояния до центра трубы плюс собственный момент инерции отверстия. Больше подробностей в статье «Моменты инерции поперечных сечений».
Если расчет не требует особой точности и диаметр отверстия в 5 и более раз меньше диаметра трубы (вроде ваш случай, если 32.39 — это наружный диаметр), то сегмент отверстия можно привести к прямоугольнику. Если отверстие не сквозное, то следует дополнительно определить положение центра тяжести трубы с отверстием для того, чтобы потом вычислить новое значение момента сопротивления.
Но и это еще не все. Вам следует учесть, что возле отверстий возникают значительные локальные напряжения.
09-10-2015: Борис
Неравноплечий уголок.При вычислении Wy не y,а H-y
09-10-2015: Доктор Лом
Не пойму, о чем вы. Определение момента сопротивления относительно оси у в таблицах вообще не приводится.
09-10-2015: Борс
Для треугольников при вычислении Wzп h в квадрате.
09-10-2015: Борис
Пардон,Wz
09-10-2015: Доктор Лом
Все верно. Теперь понял, о чем вы. Более корректно было бы указать момент сопротивления для верхней и для нижней части сечения, а я указал только для нижней. Ну а при определении момента сопротивления треугольников банально пропущен квадрат.
Исправил. Спасибо за внимательность.
28-04-2016: Jama
Здравствуете! Кто может помочь о правильности расчета http://ej.kubagro.ru/2011/02/pdf/19.pdf
я не могу понят откуда значение берется момент сопротивления. Помогите пожалуйста!
28-04-2016: Доктор Лом
Что именно вам не понятно (вычитывать весь документ у меня нет времени). Если речь о балке, лежащей на упругом основании, то скорее всего балка эта имеет прямоугольное сечение (см. таблицу 1).
29-08-2016: Максим
Здравствуйте ! Имеется швеллер № 12. В верхний пояс будут вкручиваться саморезы и винты для крепления кровли. Как учесть ослабление швеллера, т.е как определить W ослабленного сечения.
29-08-2016: Доктор Лом
Если максимально упростить, то:
Сначала определяете момент инерции отверстия (для упрощения расчетов его можно принимать прямоугольным). Затем из момента инерции швеллера вычитаете момент инерции отверстия, затем делите полученный момент инерции на половину высоты швеллера и получаете момент сопротивления.
21-03-2017: игорь
здравствуйте,Сергей. я прочитал некоторые ваши статьи,очень интересно и понятно(в основном).я хотел бы рассчитать балку двутаврового сечения,но не могу найти Ix и Wx. дело в том что она не стандартная,я её буду делать сам,из дерева.можете ли вы мне помочь? я оплачу.только я не смогу оплатить электронными средствами т.к. не знаю как этим пользоваться.
21-03-2017: Доктор Лом
Игорь, я отправил вам письмо.
30-08-2017: Али
Уважаемый доктор, желаю вам всего найлучшего. Помогите пожалуйста, какими формулами нужны для подбора и проверки на прочность балку следующих сечений,:Швеллер,уголок и бульбовый профиль, имея допускаемый момент сопротивления W=58,58cm3. спасибо большое и жду вашу помощь.
31-08-2017: Доктор Лом
Посмотрите статью «Расчет стальных однопролетных балок с шарнирными опорами при изгибе согласно СП 16.13330.2011», там все достаточно подробно расписано.
13-11-2017: Абдуахад
Здравствуйте пожалуйста подскажите почему Ql^2/8 почему деленная на 8 и почему иногда делим на 6 и 24 итд подскажите пожалуйста только это не понял
