Теплоотдача 1 м стальной трубы – проводим расчет
Расчёт теплоотдачи трубы требуется при проектировании отопления, и нужен, чтобы понять, какой объём тепла потребуется, чтобы прогреть помещения и, сколько времени на это уйдёт. Если монтаж производится не по типовым проектам, то такой расчёт необходим.
Стальная труба
Для каких систем нужен расчёт?
Коэффициент теплоотдачи считается для тёплого пола. Всё реже эта система делается из стальных труб, но если в качестве теплоносителей выбраны изделия из этого материала, то произвести расчёт необходимо. Змеевик – ещё одна система, при монтаже которой необходимо учесть коэффициент отдачи тепла.
Радиатор из стальных труб
Регистры – представлены в виде толстых труб, соединённых перемычками. Теплоотдача 1 метра такой конструкции в среднем – 550 Вт. Диаметр же колеблется в пределах от 32 до 219 мм. Сваривается конструкция так, чтобы не было взаимного подогрева элементов. Тогда теплоотдача увеличивается. Если грамотно собрать регистры, то можно получить хороший прибор обогрева помещения – надёжный и долговечный.
Как оптимизировать теплоотдачу стальной трубы?
В процессе проектирования перед специалистами встаёт вопрос, как уменьшить или увеличить теплоотдачу 1 м. стальной трубы. Для увеличения требуется изменить инфракрасное излучение в большую сторону. Делается это посредством краски. Красный цвет повышает теплоотдачу. Лучше, если краска матовая.
Расчет
Другой подход – установить оребрение. Оно монтируется снаружи. Это позволит увеличить площадь теплоотдачи.
В каких же случаях требуется параметр уменьшить? Необходимость возникает при оптимизации участка трубопровода, расположенного вне жилой зоны. Тогда специалисты рекомендуют утеплить участок – изолировать его от внешней среды. Делается это посредством пенопласта, специальных оболочек, которые производятся из особого вспененного полиэтилена. Нередко используется и минеральная вата.
Производим расчёт
Формула, по которой считается теплоотдача следующая:
Q = K*F*dT, где
- К – коэффициент теплопроводности стали;
- Q – коэффициент теплоотдачи, Вт;
- F – площадь участка трубы, для которого производится расчёт, м2 dT – величина напора температуры (сумма первичной и конечной температур с учётом комнатной температуры), ° C.
Коэффициент теплопроводности K выбирается с учётом площади изделия. Зависит его величина и от количества ниток, проложенных в помещениях. В среднем величина коэффициента лежит в пределах 8-12,5.
dT называется также температурным напором. Чтобы параметр высчитать, нужно сложить температуру, которая была на выходе из котла, с температурой, которая зафиксирована на входе в котёл. Полученное значение умножается на 0,5 (или делится на 2). Из этого значения вычитается комнатная температура.
dT = (0,5*(T1 + T2)) — Tк
Если стальная труба изолирована, то полученное значение умножается на КПД теплоизоляционного материала. Он отражает процент тепла, который был отдан при прохождении теплоносителя.
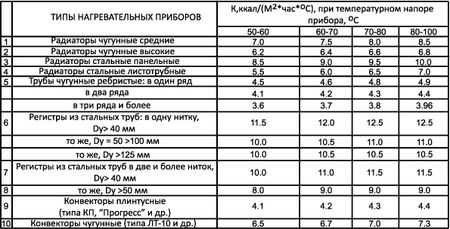
Рассчитываем отдачу для 1 м. изделия
Посчитать теплоотдачу 1 м. трубы, выполненной из стали, просто. У нас есть формула, осталось подставить значения.
Q = 0,047*10*60 = 28 Вт.
Здесь
- К = 0.047, коэффициент теплоотдачи;
- F = 10 м2, площадь трубы;
- dT = 60° С, температурный напор.
Об этом стоит помнить
Хотите сделать систему отопления грамотно? Не стоит подбирать трубы на глазок. Расчёты теплоотдачи помогут оптимизировать траты на строительство. При этом можно получить хорошую отопительную систему, которая прослужит долгие годы.
trubygid.ru
как расчитать и увеличить, от чего зависит
Теплоотдача 1 м стальной трубы – проводим расчет

Производим расчёт
Q = K*F*dT, где
- F – площадь участка трубы, для которого производится расчёт, м2 dT – величина напора температуры (сумма первичной и конечной температур с учётом комнатной температуры), ° C.

dT = (0,5*(T1 + T2)) — Tк

Q = 0,047*10*60 = 28 Вт.
- F = 10 м2, площадь трубы;
Об этом стоит помнить
Хотите сделать систему отопления грамотно? Не стоит подбирать трубы на глазок. Расчёты теплоотдачи помогут оптимизировать траты на строительство. При этом можно получить хорошую отопительную систему, которая прослужит долгие годы.
trubygid.ru
Теплые водяные полы – это удобный и недорогой способ обогрева дома или квартиры. При этом наиболее надежны и экономичны теплые водяные полы, подключенные к системе отопления или отдельному отопительному контуру с питанием от котла. Затраты при выполнении такого пола вполне оправданы, ведь в процессе эксплуатации они окупаются очень быстро. При этом значительную часть затрат составляют затраты на трубы для выполнения греющего контура.

Какие трубы лучше для теплого пола? Это зависит от нескольких факторов: от способа укладки, длины контура, способа выполнения стяжки и финишного покрытия. Существует несколько видов применяемых труб:
- Медные;
- Металлопластиковые;
Все они имеют свои особенности, которые необходимо учесть при выборе.
Медные трубы
Их отличает высокое качество, отличная теплоотдача, прочность и долговечность, но при этом максимальная из возможных вариантов цена и некоторая сложность в монтаже: гибку труб необходимо производить по шаблону, а для стыков использовать сварку. Кроме того, если греющий контуртеплого пола подключен к системе отопления с алюминиевыми или стальными радиаторами, возможно возникновение гальванической пары, что приведет к электрохимической коррозии радиаторов.

Медные трубы для теплого пола применяют обычно там, где требуется максимально быстрый прогрев помещения при минимальных тепловых потерях. Это актуально для домов, в которых ввиду невозможности установки газового котла теплоноситель получают более дорогостоящим способом: с помощью дизельного или электрического котла. Затраты на медные трубы в 5-7 раз выше, чем на металлопластиковые или полиэтиленовые. При этом температуру теплоносителя для медных труб можно поддерживать на 5-10 градусов меньше, что в конечном итоге приведет к их окупаемости в течение двух-трех лет.
Для теплого пола применяют медные трубы диаметром 20 мм, стараясь сделать минимальное количество стыков. Из-за высокой теплоотдачи температура в начальной части контура может быть значительно выше, чем в конце, из-за чего пол прогревается неравномерно в разных зонах. Поэтому предпочтительнее укладывать медные трубы «улиткой» или «двойной змейкой», чтобы рядом проходили как прямая, так и обратная части контура.

Металлопластиковые трубы
Металлопластиковые трубы состоят из термостойкого пластика, армированного сплошным или сетчатым металлическим слоем. Их внутренняя поверхность гладкая, на ней не образуется отложений, что позволяет сохранить постоянный рабочий просвет в течение всего срока службы. Для теплого пола необходимо выбирать трубы, предназначенные именно для горячего теплоносителя.

Металлопластиковые трубы для теплого пола – самый простой вариант для самостоятельного монтажа. Присоединение греющего контура к прямому и обратному коллектору производится с помощью обжимных фитингов без применения специального инструмента, к тому же трубы при гибке сохраняют форму, и их можно укладывать силами одного человека. При этом металлопластиковые трубы имеют два существенных недостатка:
- фитинги в процессе эксплуатации требуют периодической затяжки, поэтому необходимо обеспечить беспрепятственный к ним доступ;
- при выполнении стяжки нужно следить, чтобы не смять трубы и не сузить их просвет.
Теплоотдача у металлопластиковых труб несколько ниже, чем умедных, однако это компенсируется их невысокой стоимостью и удобством монтажа. Наиболее удобно монтировать металлопластиковые трубы на специальные теплоизолирующие маты с бобышками – их просто укладывают в промежутки между бобышками, создавая необходимый контур, а поверх заливают бетонную стяжку. При таком способе укладки вероятность их повреждения минимальна.

При выборе производителя металлопластиковых труб лучше отдать предпочтение проверенным фирмам, а сами трубы выбрать с кислородонепроницаемым слоем – это продлит срок службы стальных элементов греющего контура. Диаметр труб для греющего контура – 20 мм.
Полиэтиленовые трубы
Один из самых популярных видов выполнения теплого пола подразумевает использование труб из шитого полиэтилена. Эти трубы наиболее дешевые, легко монтируются, обладают упругостью и не боятся сминания при выполнении стяжки. Теплоотдача у полиэтилена ниже, чем у медн
tmzs.ru
Расчет стационарной теплопроводности и теплопередач. Задание №1 Вариант 4
Теплота передается через стенку стальной
трубы толщиной  мм
(
мм
(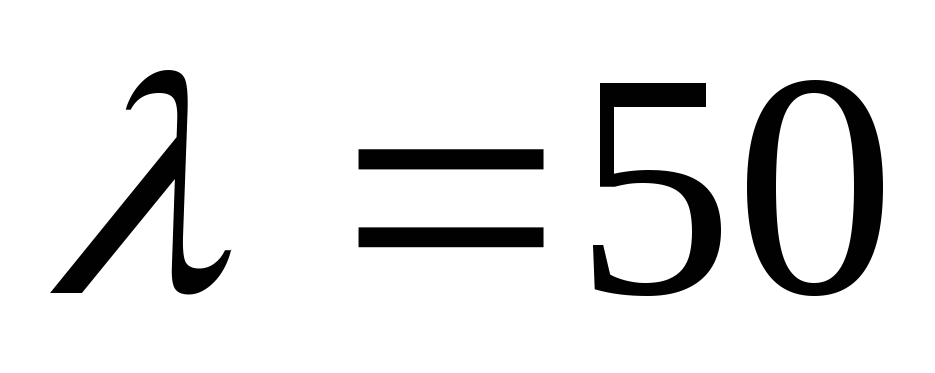
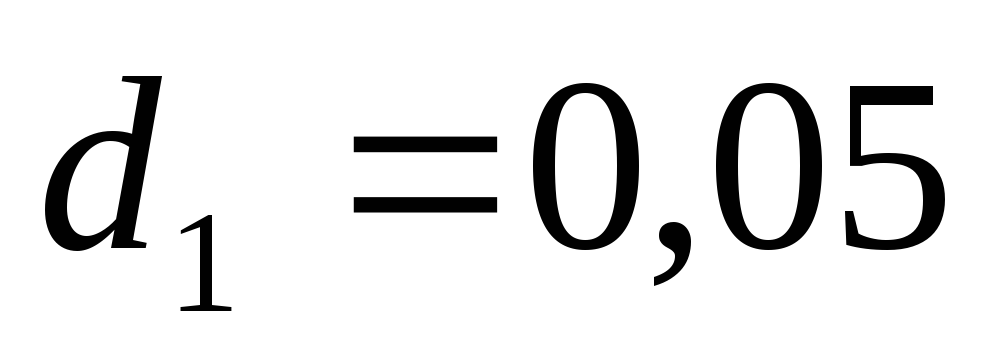 ,
температура дымовых газов
,
температура дымовых газов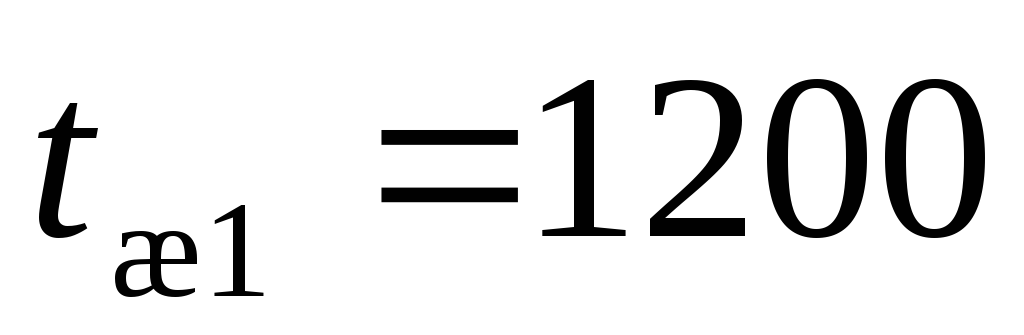 ,
ºС, температура кипящей воды
,
ºС, температура кипящей воды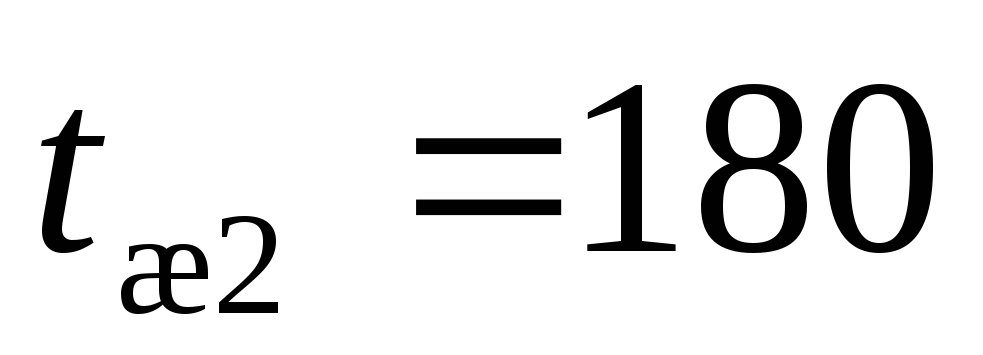 ,
ºС, коэффициент теплоотдачи от дымовых
газов к наружной поверхности трубы
,
ºС, коэффициент теплоотдачи от дымовых
газов к наружной поверхности трубы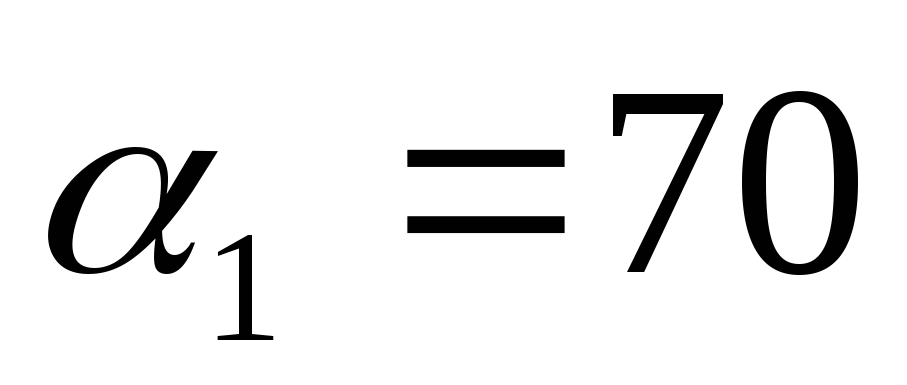 ,
Вт/м²·К, коэффициент теплоотдачи от
внутренней поверхности трубы к воде
,
Вт/м²·К, коэффициент теплоотдачи от
внутренней поверхности трубы к воде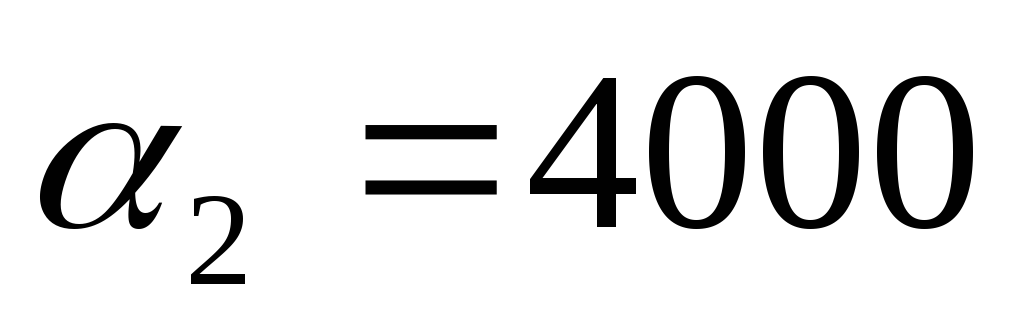
Рассчитать :
-коэффициент теплопередачи (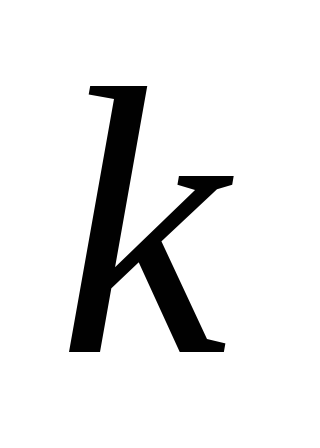 ,
Вт/м²·К) от газов к воде,
,
Вт/м²·К) от газов к воде,
-линейную плотность теплового потока
(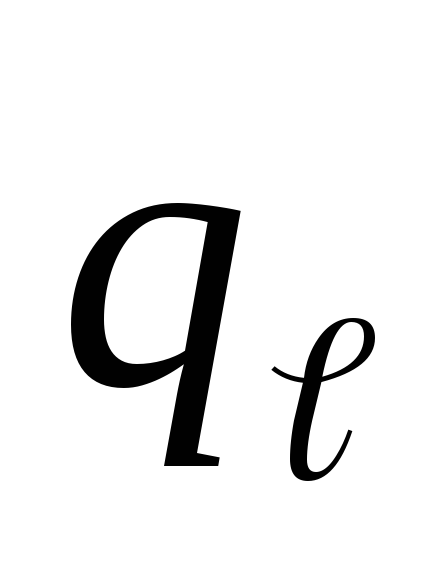 ,
Вт/м),
,
Вт/м),
-температуры на внутренней поверхности
трубы 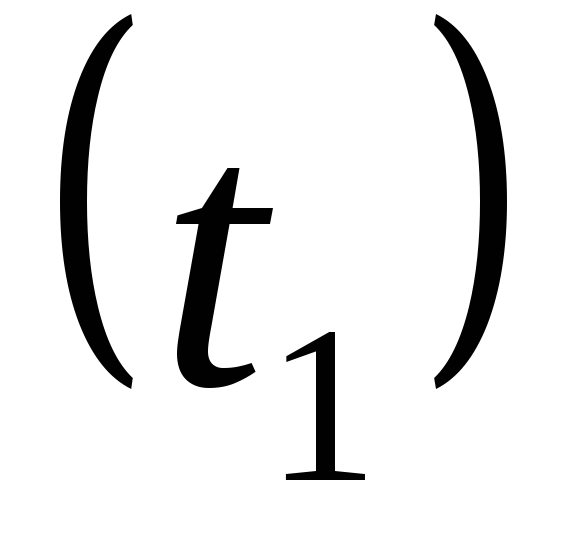 и на наружной поверхности
и на наружной поверхности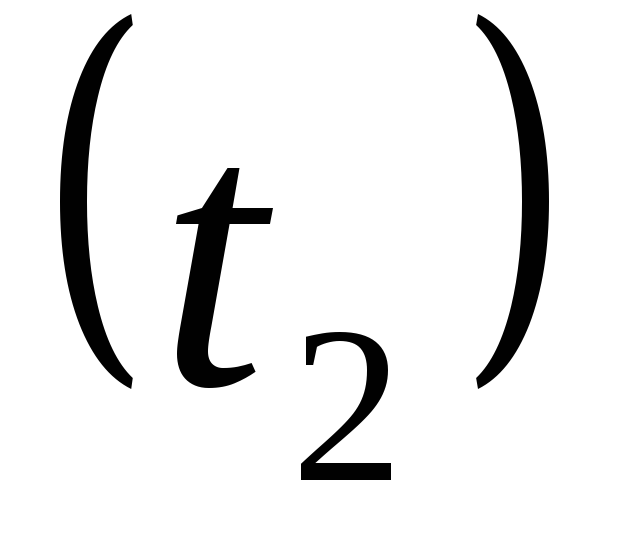
Построить график распределения температур
по толщине стенки. Нанести на график
температуры 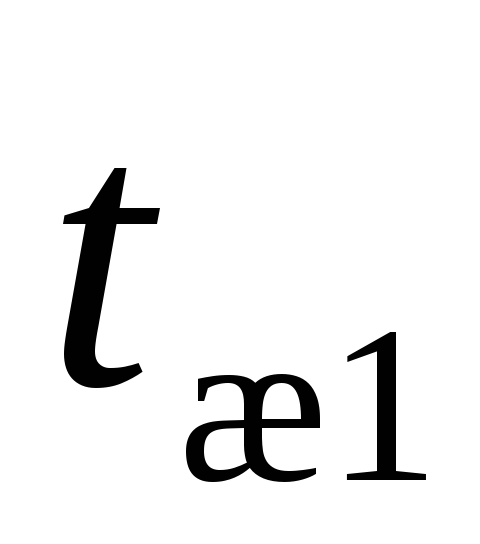
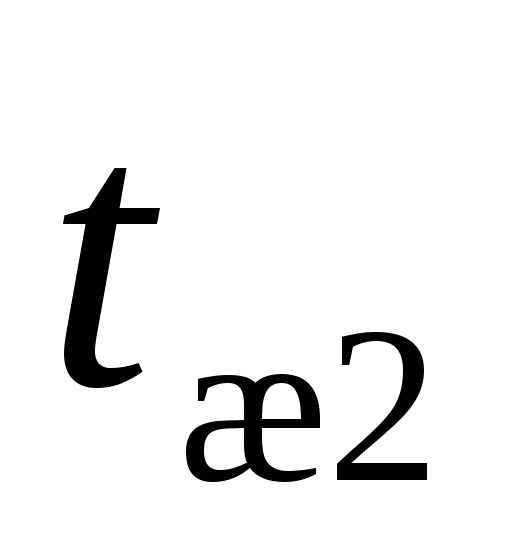 .
. В процессе эксплуатации на внутренней
поверхности образовался слой накипи
толщиной 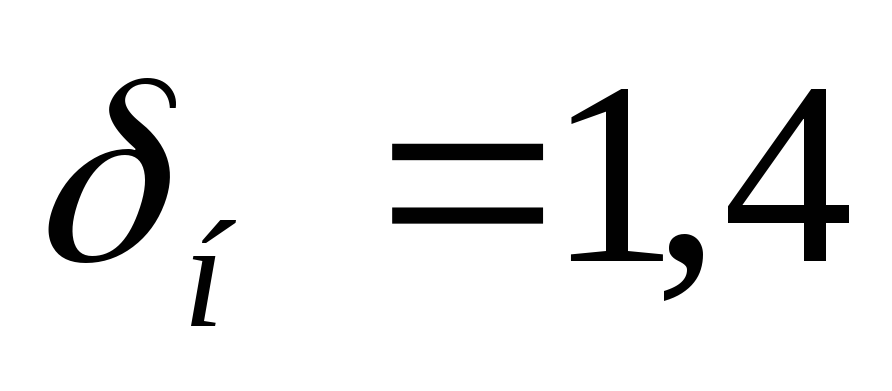 мм.
мм.
Рассчитать для этого случая  ,
, ,
,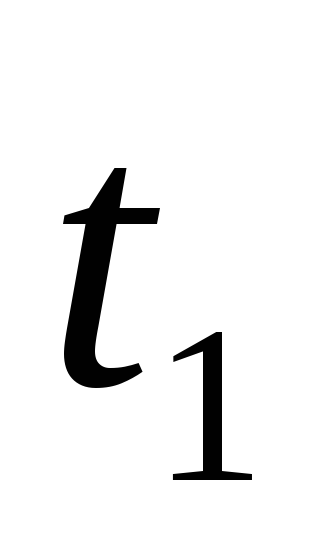 ,
,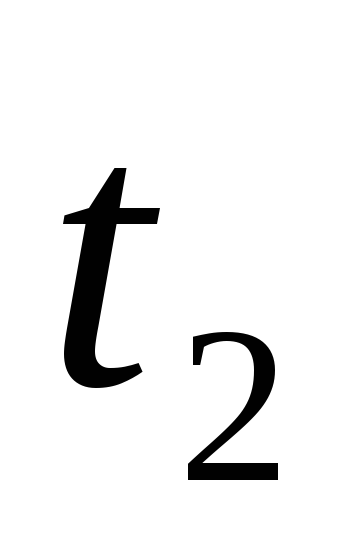
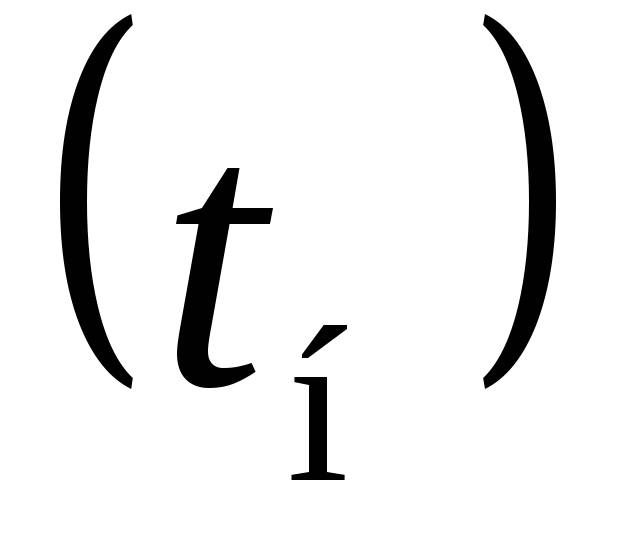 .
. Принять коэффициент теплопроводности
накипи 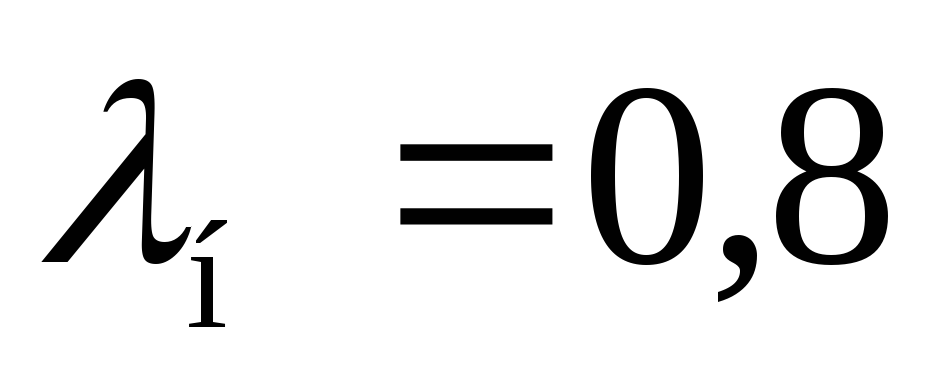 Вт/м·К.
Вт/м·К.
Построить график распределения температур по толщине стенки и накипи. Дать сравнительный анализ двух графиков.
Определяем внешний диаметр трубы 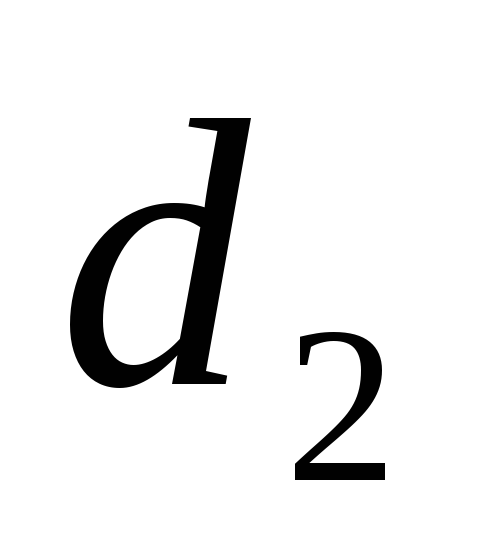
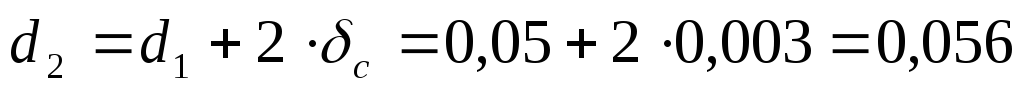 м
м
Определим коэффициент теплопередачи 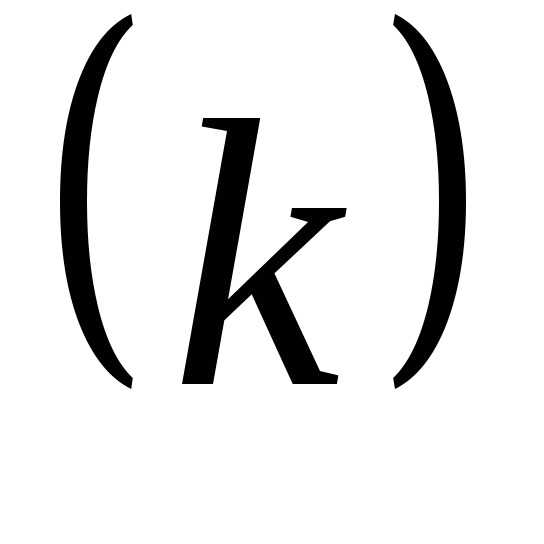 от дымовых газов к воде через стенку
трубы
от дымовых газов к воде через стенку
трубы
 Вт/м²·К
Вт/м²·К
Определим линейную плотность теплового
потока 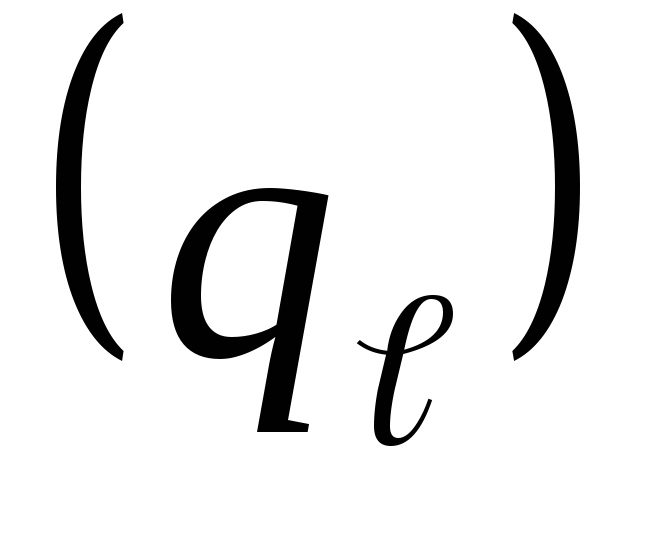 для случая трубы без накипи
для случая трубы без накипи
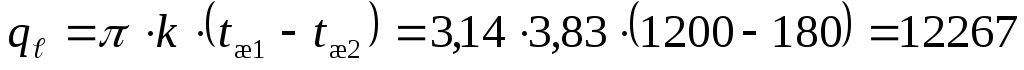 Вт/м
Вт/м
Определим температуры на внутренней
поверхности трубы 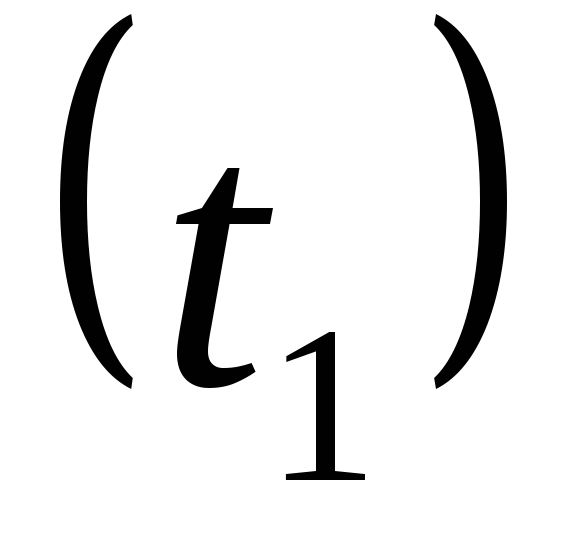 и наружной поверхности трубы
и наружной поверхности трубы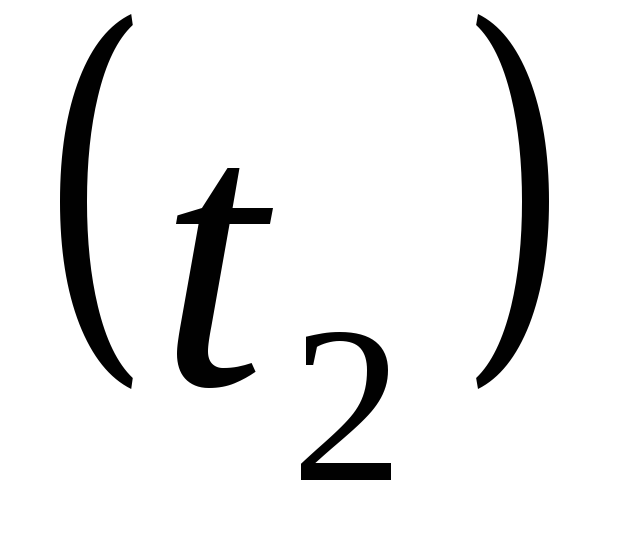
Температура на внутренней поверхности
трубы 
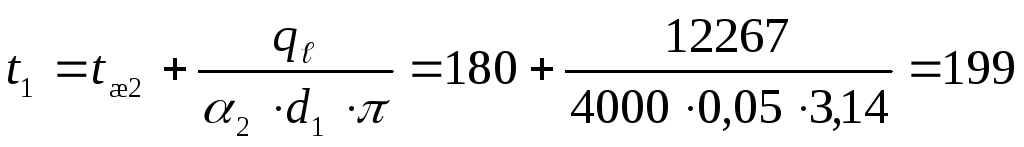 ,
ºС
,
ºС
Температура на наружной поверхности
трубы 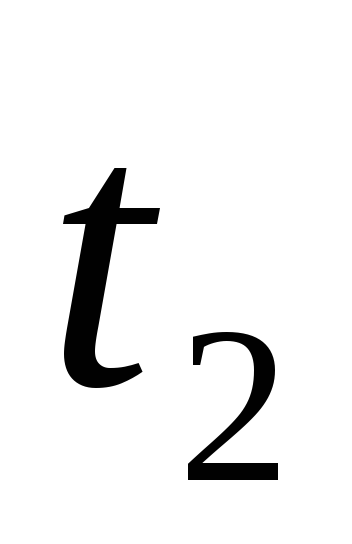
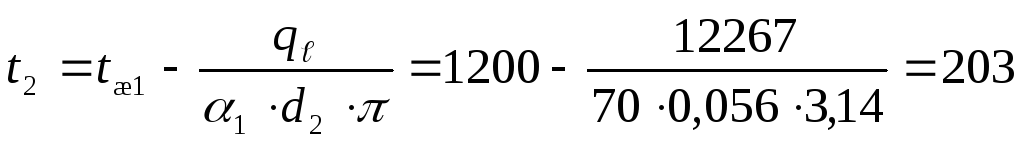 ,
ºС
,
ºС
В процессе эксплуатации на внутренней
поверхности трубы образовалась накипь
толщиной 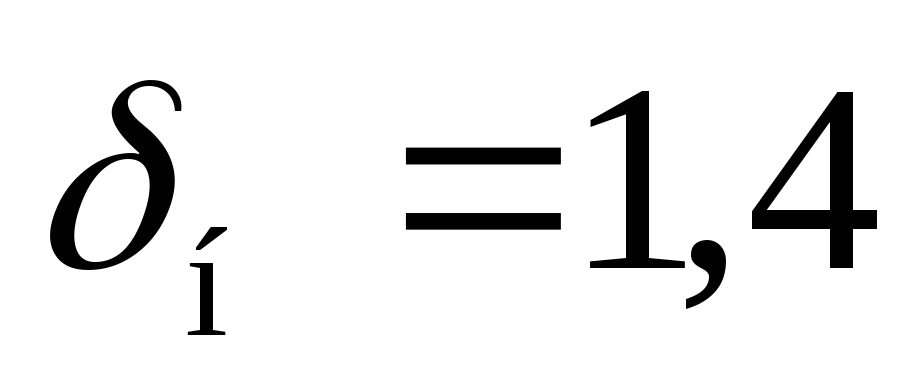 мм.
Коэффициент теплопроводности накипи
мм.
Коэффициент теплопроводности накипи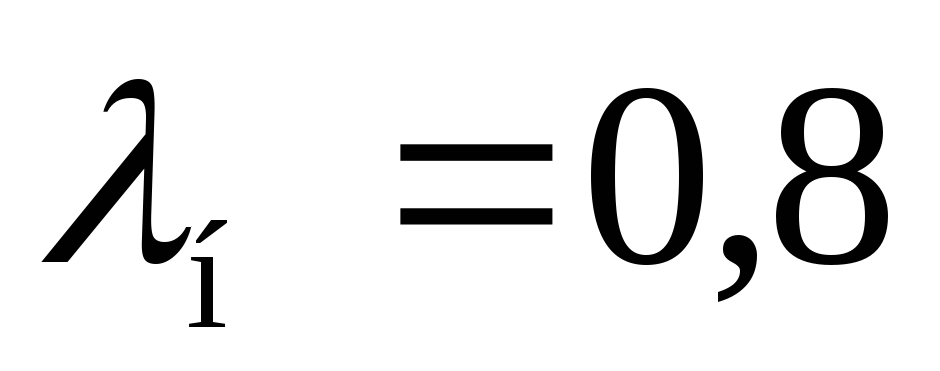 Вт/м·К
Вт/м·К
Определим внутренний диаметр накипи 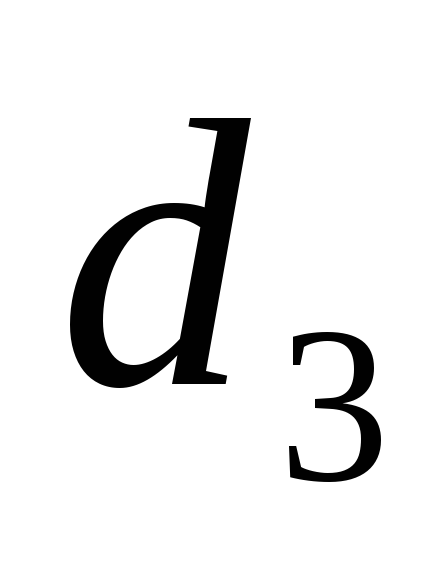
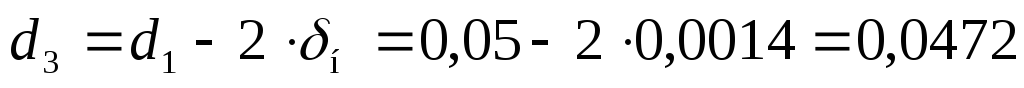 ,
м
,
м
Определим коэффициент теплопередачи для трубы с накипью
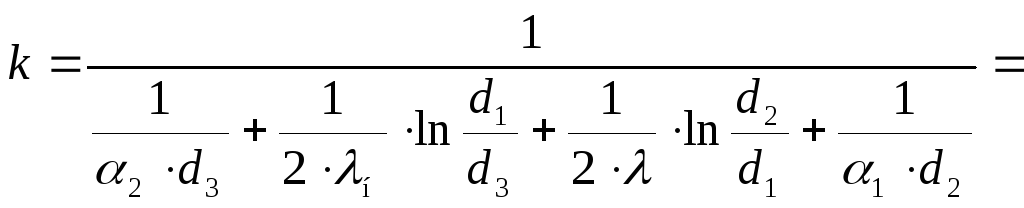
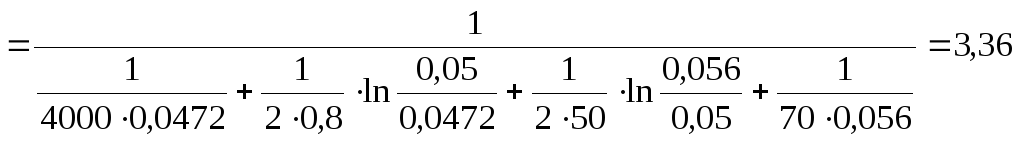 ,
Вт/м²·К
,
Вт/м²·К
Определим линейную плотность теплового
потока 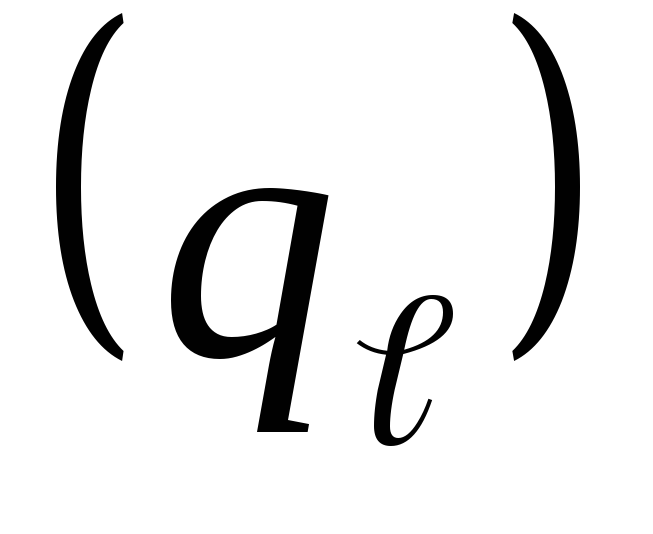 для трубы с накипью
для трубы с накипью
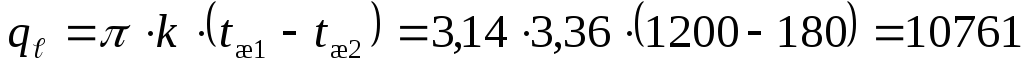 ,
Вт/м
,
Вт/м
Определим температуру на внутренней
поверхности трубы 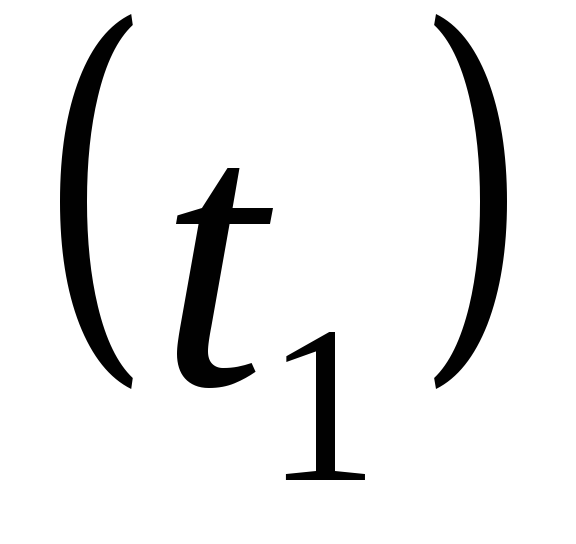 ,
температуру на наружной поверхности
трубы
,
температуру на наружной поверхности
трубы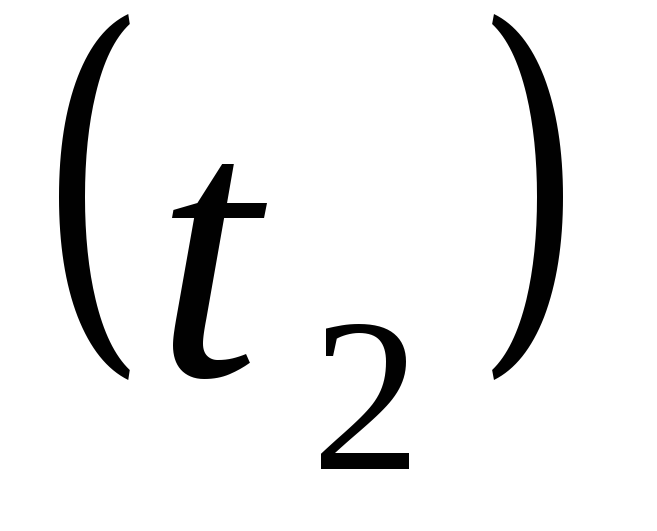 и температуру на внутренней поверхности
накипи
и температуру на внутренней поверхности
накипи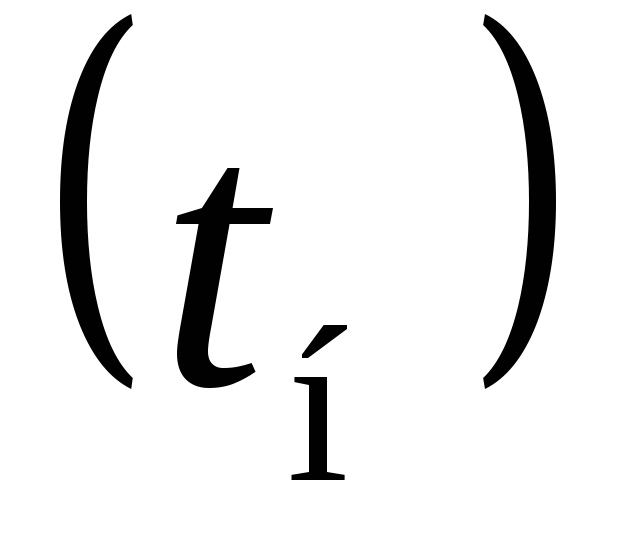
Температура на наружной поверхности
трубы 
 ,
ºС
,
ºС
Температура на внутренней поверхности
накипи 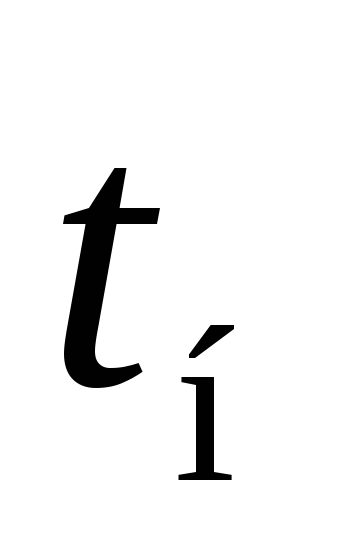
 ,
ºС
,
ºС
Температура на внутренней поверхности
трубы 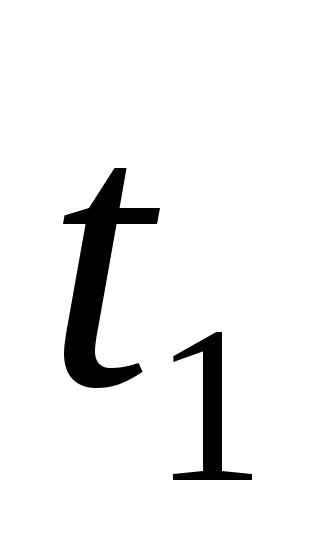
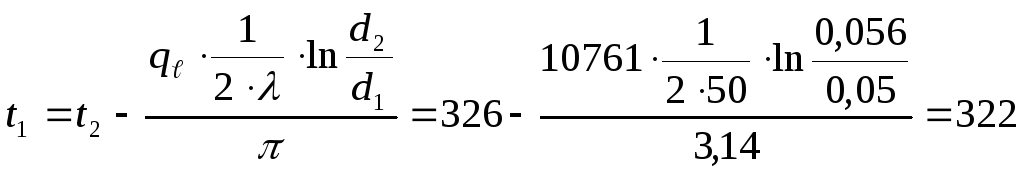 ,
ºС
,
ºС
Построим графики распределения температур по толщине стенки
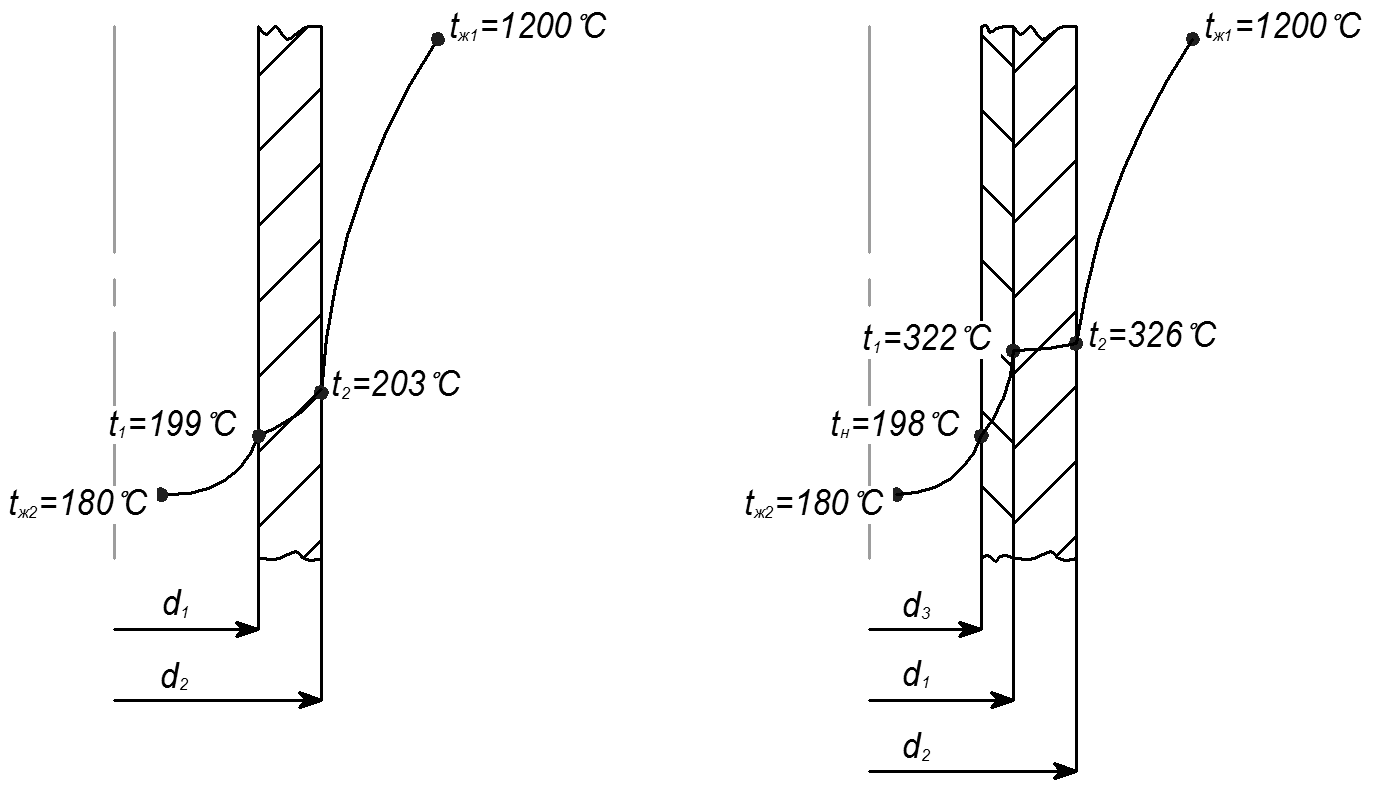
Из расчетов видно что появление накипи на внутренней поверхности трубы влечет снижение теплового потока, а из графиков видно что накипь приводит к некоторому повышению температуры поверхностей трубы.
Расчет нестационарной теплопроводности. Задание №2 Вариант 4
Нагретый шаровой калориметр из меди
диаметром 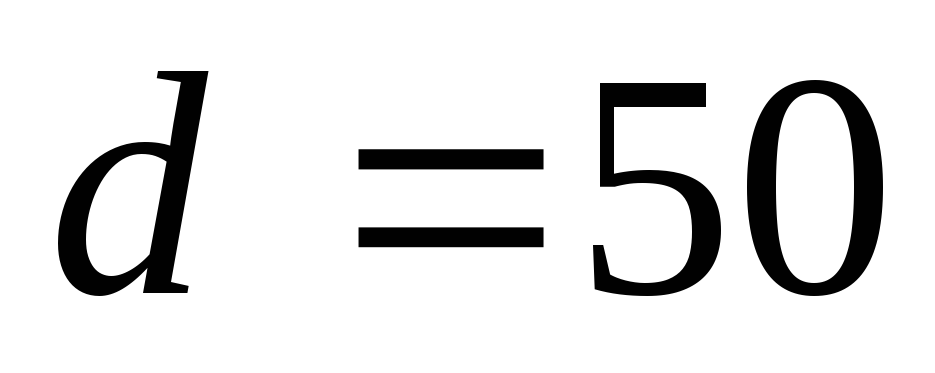 мм
с начальной температурой
мм
с начальной температурой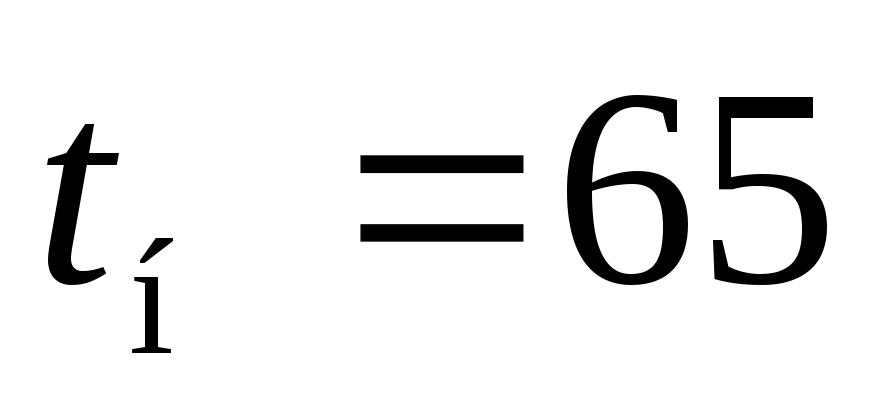 ,ºС
помещен в воду с температурой
,ºС
помещен в воду с температурой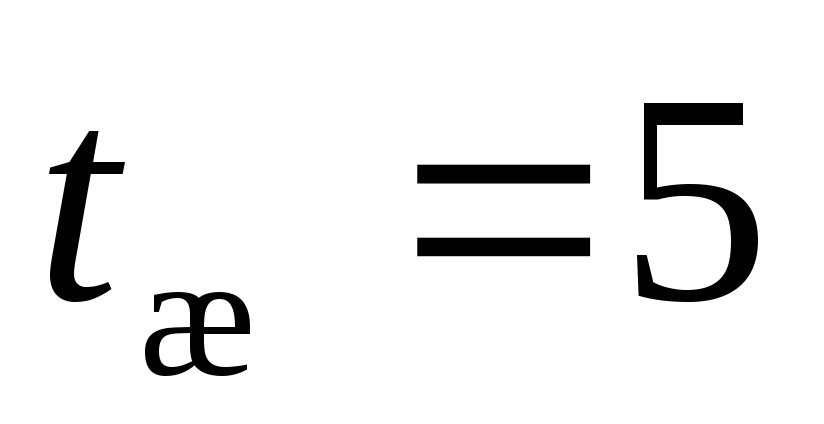 ,
ºС.
,
ºС.
Свойства меди: коэффициент теплопроводности 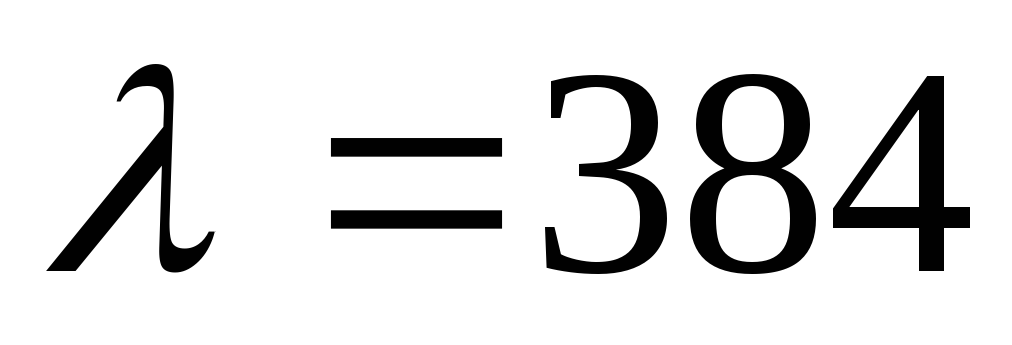 ,
Вт/м·К, удельная теплоемкость
,
Вт/м·К, удельная теплоемкость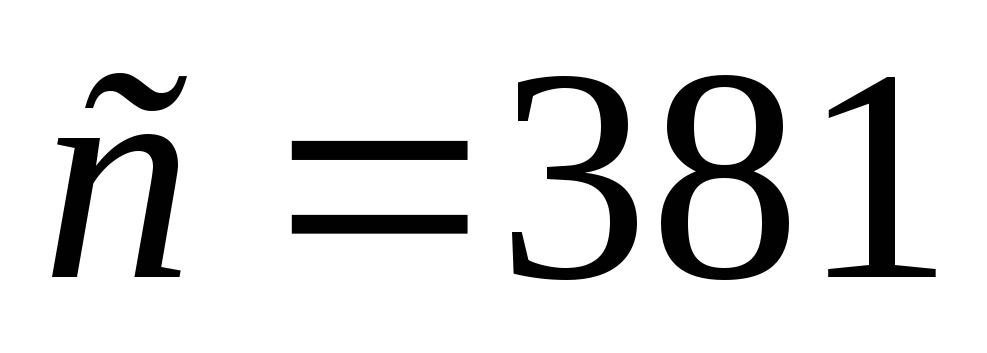 ,
Дж/кг·К, плотность
,
Дж/кг·К, плотность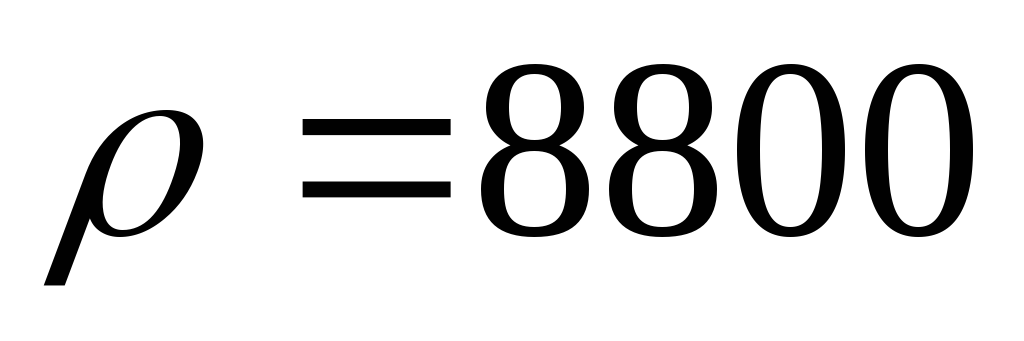 кг/м³.
кг/м³.
Коэффициент теплоотдачи поверхности
шара в процессе охлаждения 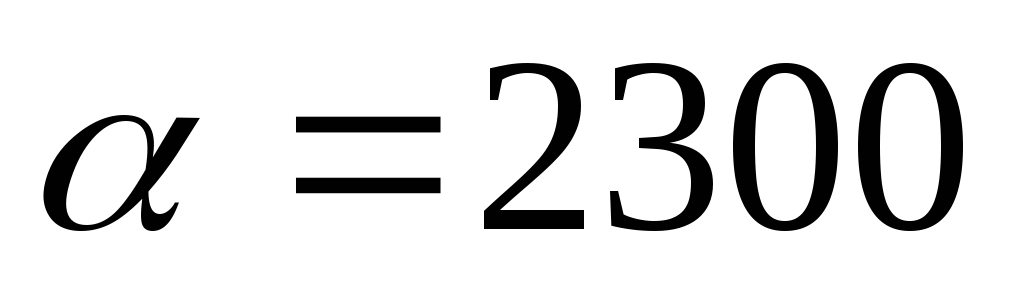 Вт/м²·К
Вт/м²·К
Определить температуры в центре 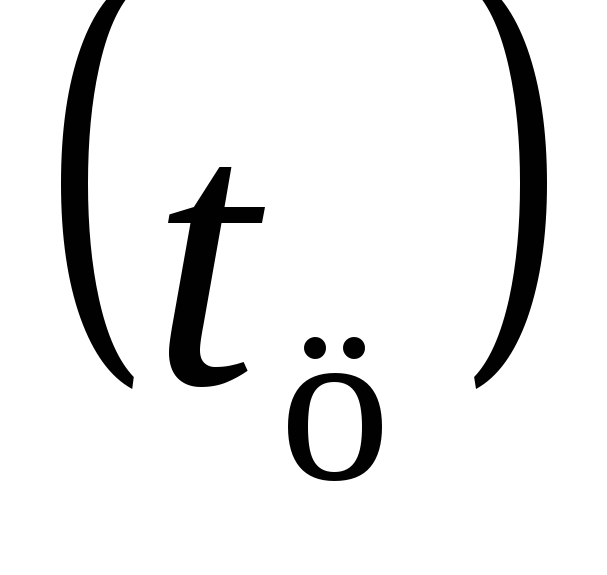 и на поверхности шара
и на поверхности шара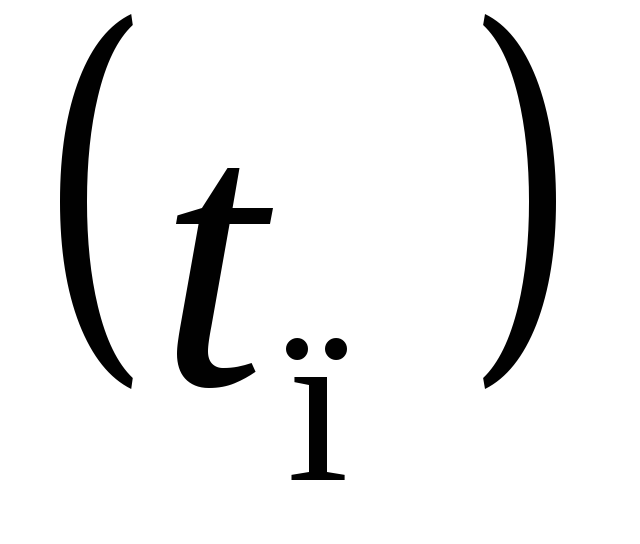 через время
через время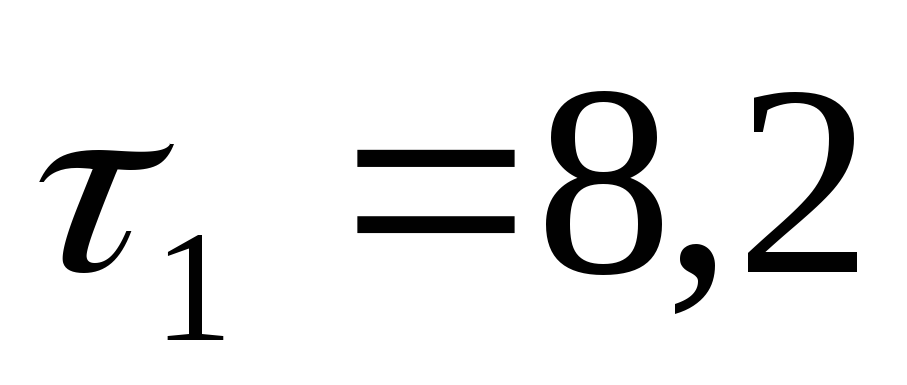 сек. После погружения его в воду.
сек. После погружения его в воду.
Изобразить график распределения
температуры по диаметру шара для моментов
времени 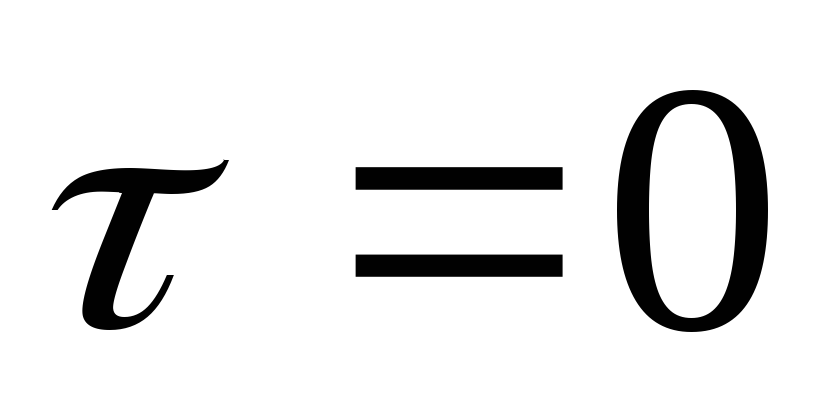 ,
,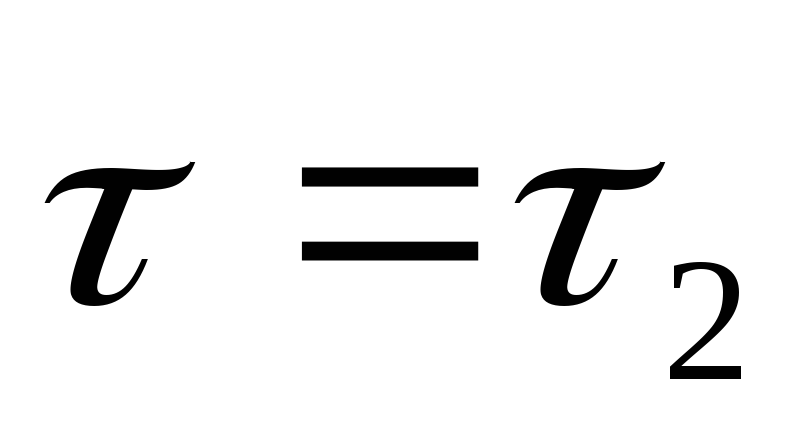 ,
, .
.
Определить полное количество тепла ( ,
Вт), отданное шаровым калориметром в
процессе его охлаждения.
,
Вт), отданное шаровым калориметром в
процессе его охлаждения.
Для определения температуры в центре
и на поверхности шара необходимо найти
безразмерные комплексы, число Био 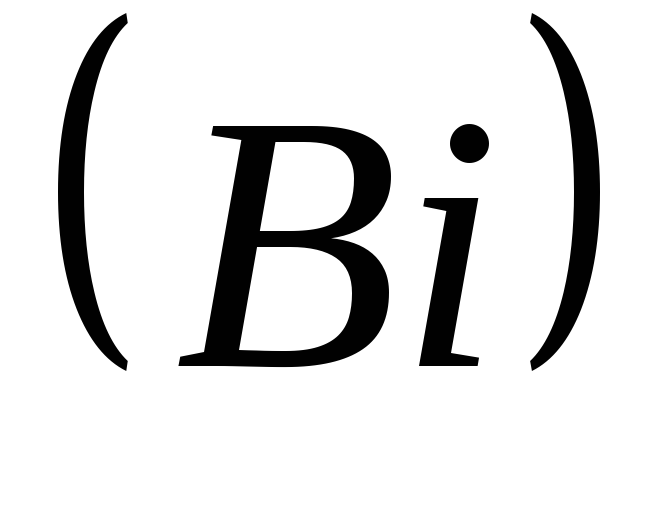 и число Фурье
и число Фурье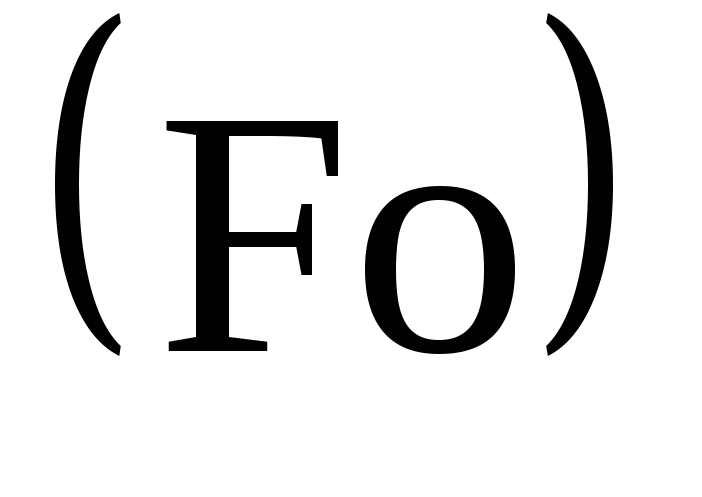
Уравнение для определения значения числа Био для шара будет иметь вид
 ,
,
где:  —
коэффициент теплоотдачи,
—
коэффициент теплоотдачи,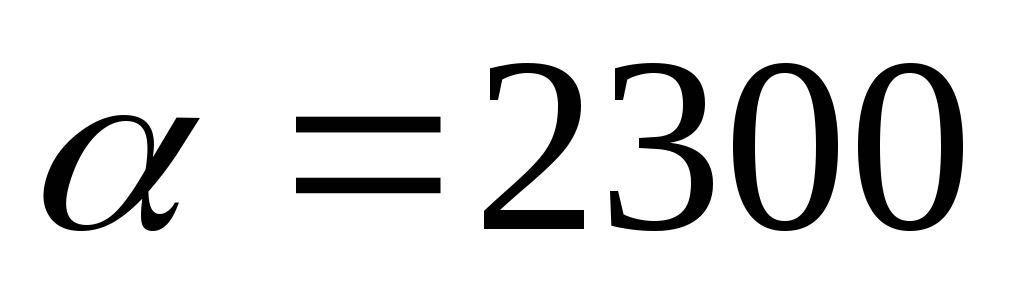 Вт/м²·К
Вт/м²·К
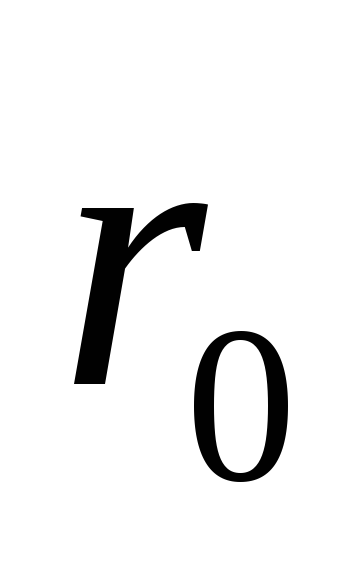 —
определяющий размер для шара это радиус,
—
определяющий размер для шара это радиус,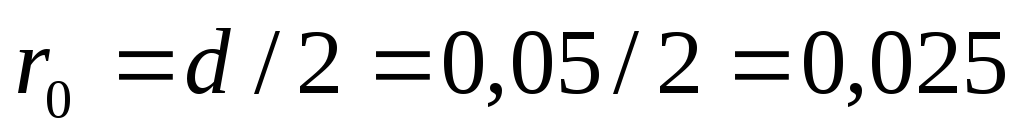 м
м
 —
коэффициент теплопроводности,
—
коэффициент теплопроводности, Вт/м·К
Вт/м·К
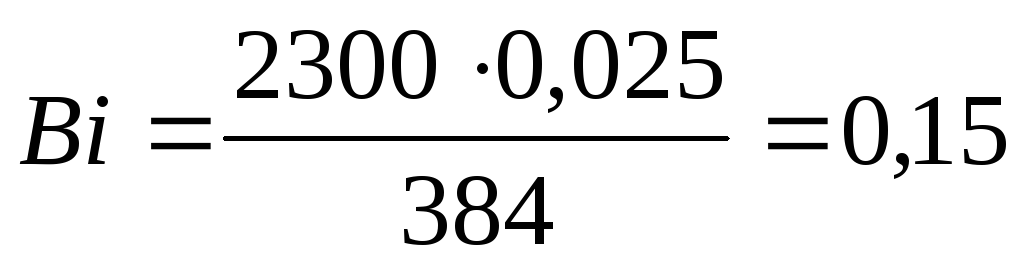
Уравнение для определения значения числа Фурье для шара будет иметь вид
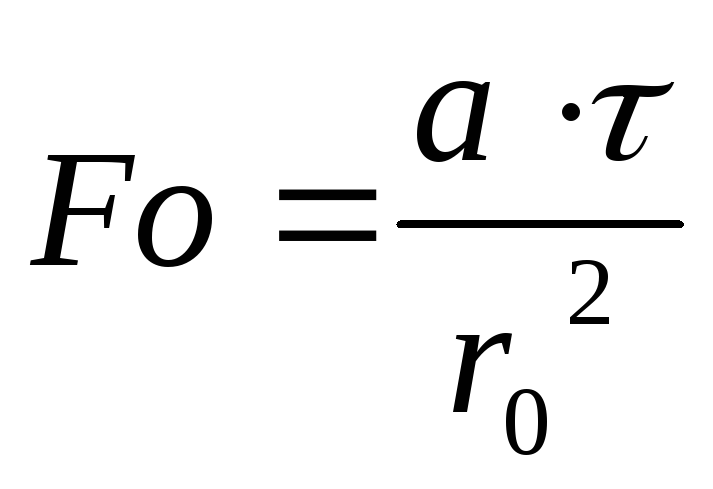 ,
,
где:  —
коэффициент температуропроводности,
м²/с
—
коэффициент температуропроводности,
м²/с
 —
время, с
—
время, с
Коэффициент температуропроводности определяется как
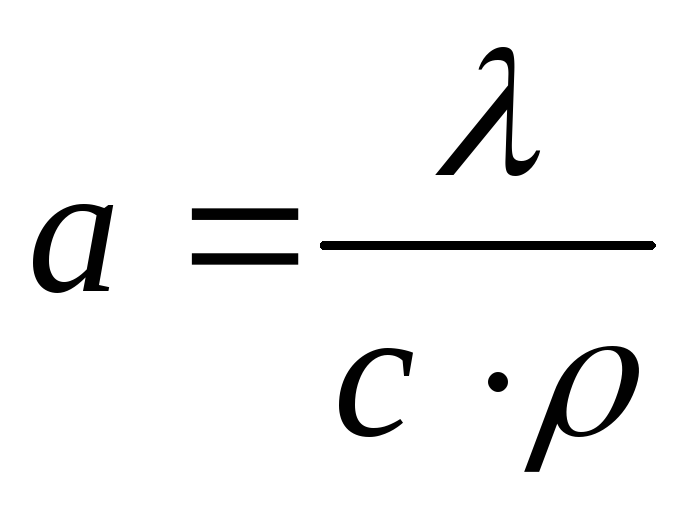 ,
м²/с
,
м²/с
где:  —
теплоемкость,
—
теплоемкость,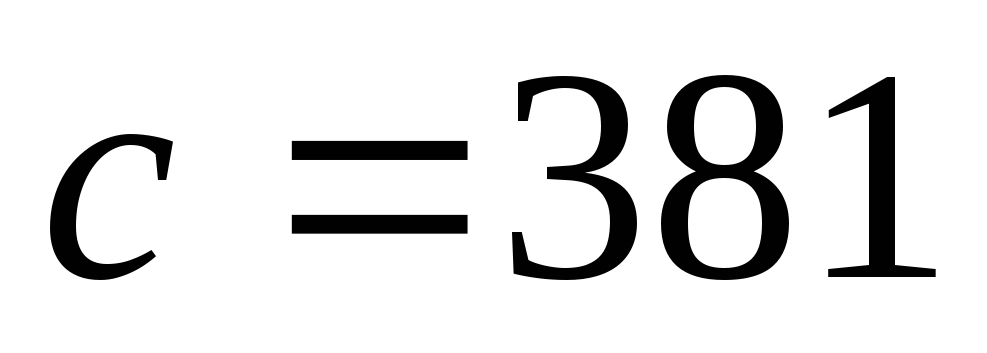 ,
Дж/кг·К
,
Дж/кг·К
 —
плотность,
—
плотность, ,
кг/м³
,
кг/м³
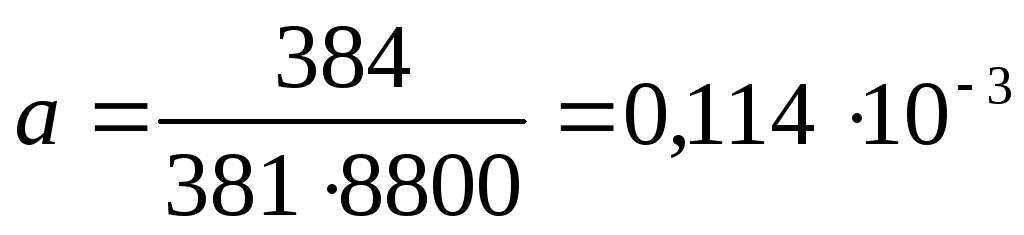 ,
м²/с
,
м²/с
Определим значение числа Фурье
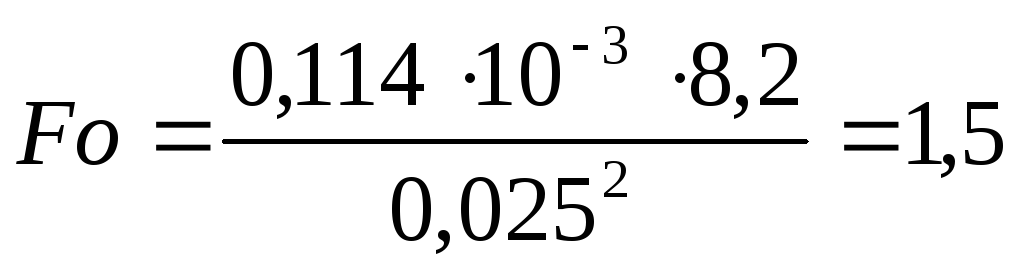
Определим безразмерную температуру 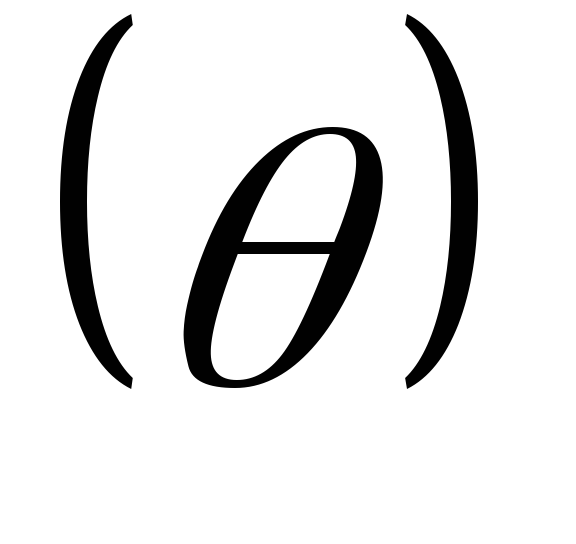 через номограммы. Значения безразмерной
температуры находится по значениям
безразмерных комплексов Фурье и Био.
через номограммы. Значения безразмерной
температуры находится по значениям
безразмерных комплексов Фурье и Био.
Для центра шара рис. 3.13 [4, стр. 86].
Значение безразмерной температуры
центра шара 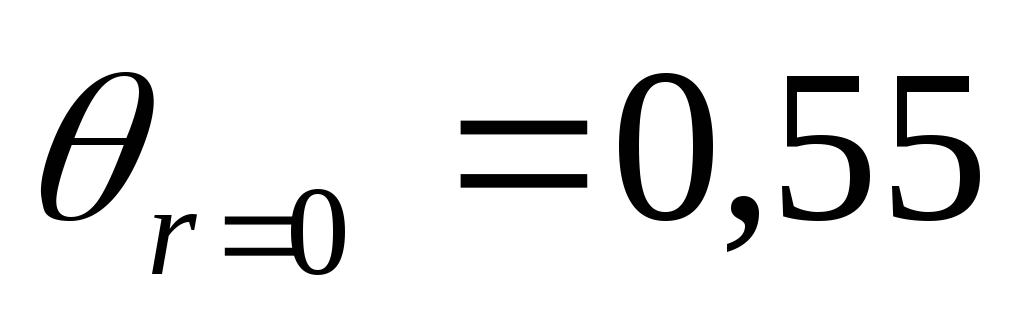
Для поверхности шара рис. 3.14 [4, стр. 86].
Значение безразмерной температуры
поверхности шара 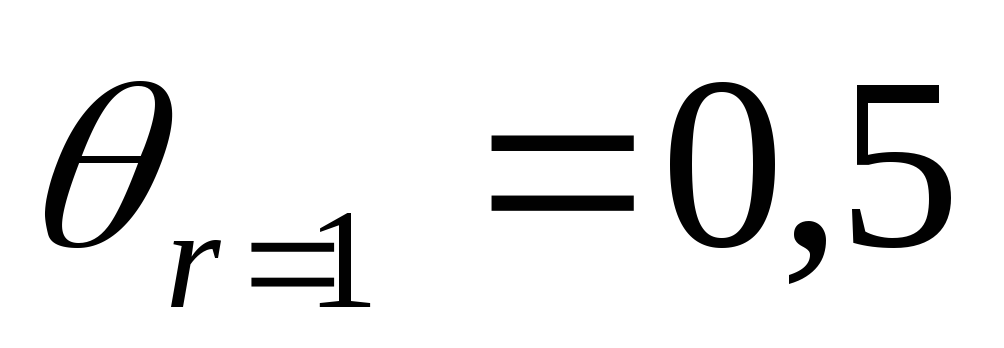
Определим температуру в центре шара
через время 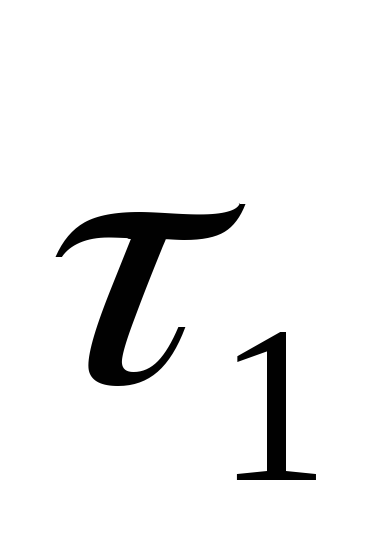
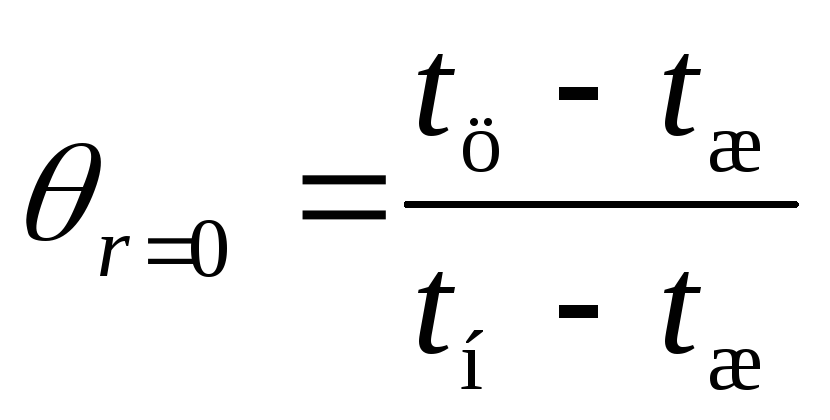

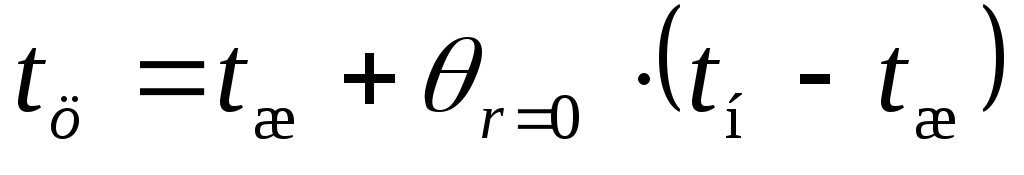
где: 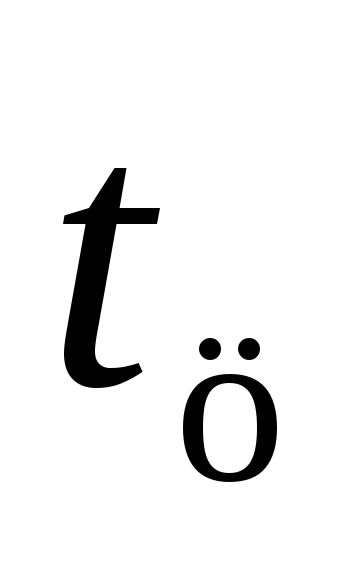 —
температура в центре шара, ºС
—
температура в центре шара, ºС
 —
температура среды в которую помещено
тело,
—
температура среды в которую помещено
тело,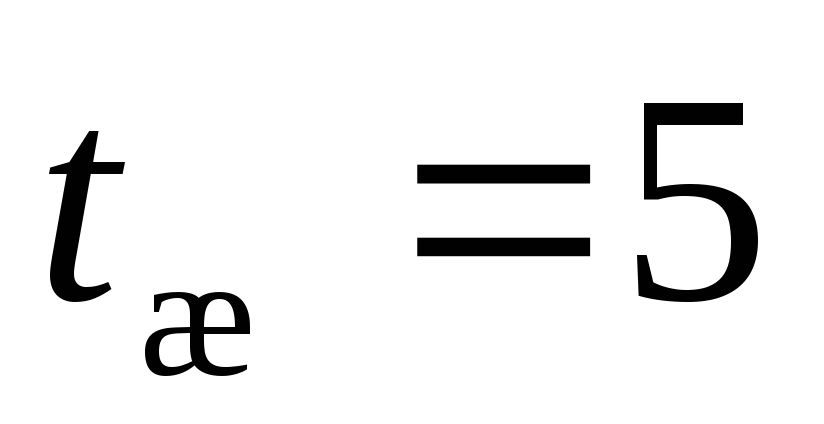 ,
ºС
,
ºС
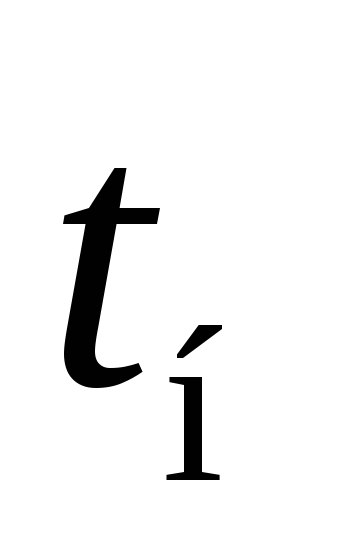 —
начальная температура тела,
—
начальная температура тела,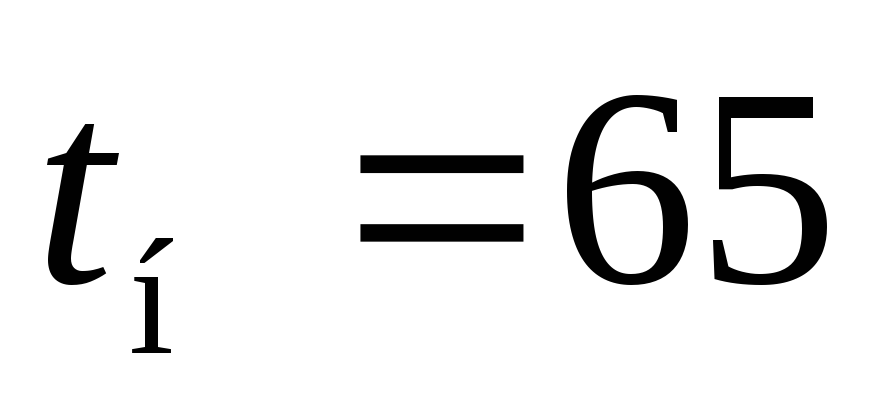 ,
ºС
,
ºС
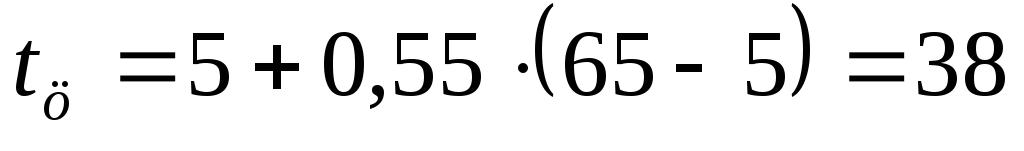 ,
ºС
,
ºС
Определим температуру на поверхности
шара через время 
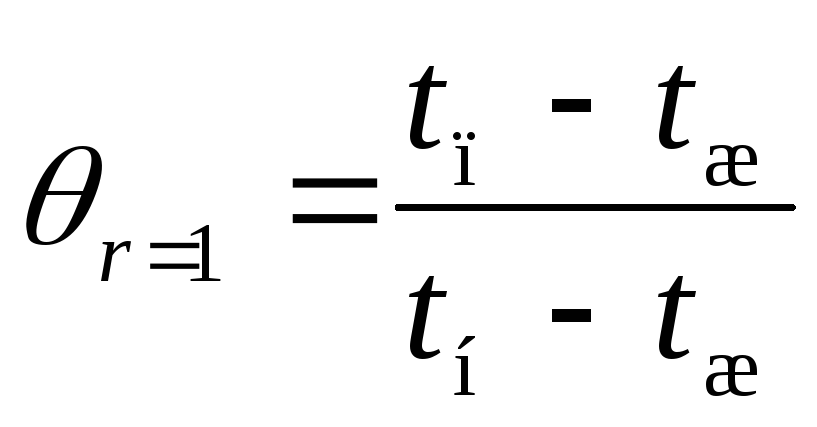

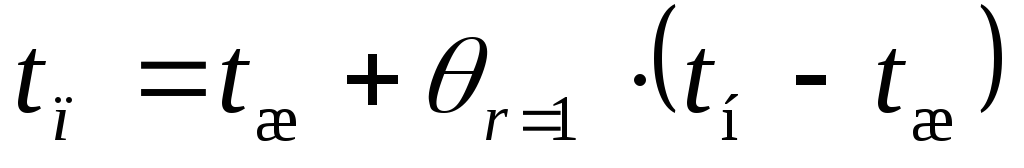
где:  —
температура на поверхности шара, ºС
—
температура на поверхности шара, ºС
 —
температура среды в которую помещено
тело,
—
температура среды в которую помещено
тело, ,
ºС
,
ºС
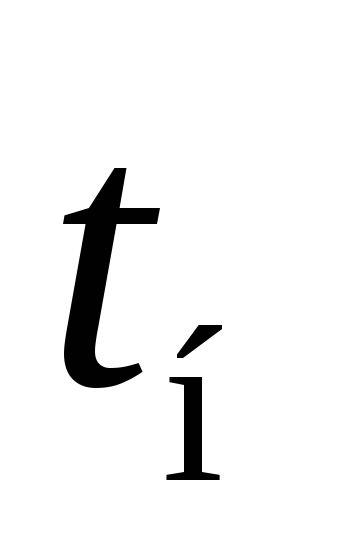 —
начальная температура тела,
—
начальная температура тела,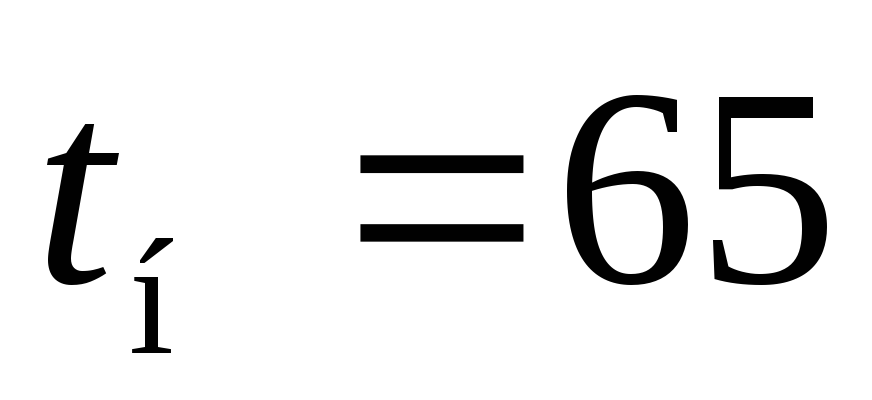 ,
ºС
,
ºС
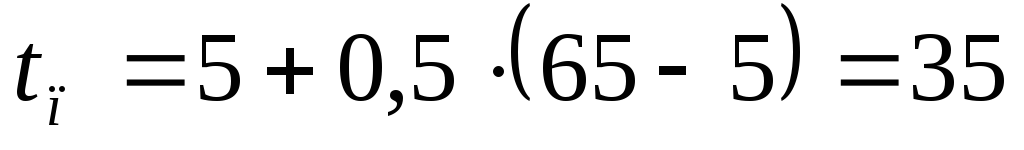 ,
ºС
,
ºС
Определим полное количество теплоты отданное от шара среде по уравнению
отданное от шара среде по уравнению
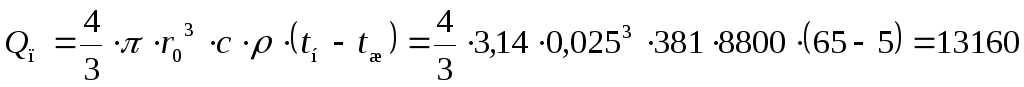 ,
Дж
,
Дж
Определим количество теплоты  отданное шаром воде за время
отданное шаром воде за время
Отношение количества теплоты  отданного за временной промежуток
отданного за временной промежуток и полного количества тепла отданного
шаром определяется по номограмме рис.
3.15 [4, стр. 86], по значению безразмерного
комплекса числа Фурье.
и полного количества тепла отданного
шаром определяется по номограмме рис.
3.15 [4, стр. 86], по значению безразмерного
комплекса числа Фурье.
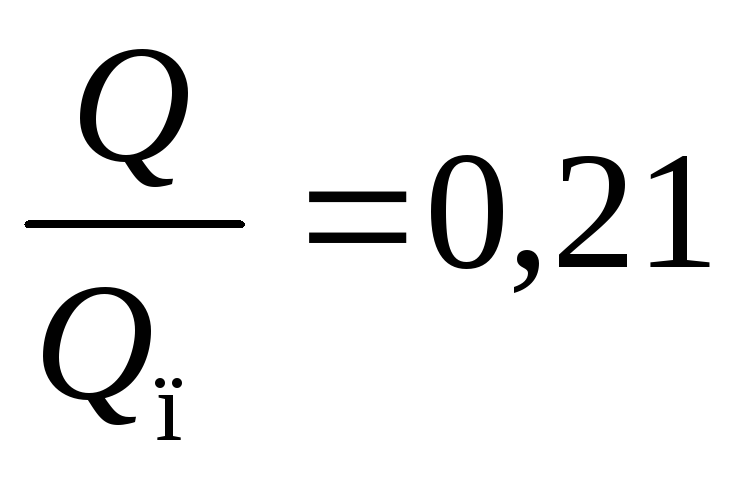
Определим теплоту отданную за время 
 ,
Дж
,
Дж
Изобразим графики распределения температуры по диаметру шара для моментов времени

studfile.net
| Материал | Плотность, кг/м3 | Теплопроводность, Вт/(м·град) | Теплоемкость, Дж/(кг·град) |
| Плита бумажная прессованая | 600 | 0.07 | — |
| Плита пробковая | 80…500 | 0.043…0.055 | 1850 |
| Плитка облицовочная, кафельная | 2000 | 1.05 | — |
| Плитка термоизоляционная ПМТБ-2 | — | 0.04 | — |
| Плиты алебастровые | — | 0.47 | 750 |
| Плиты из гипса ГОСТ 6428 | 1000…1200 | 0.23…0.35 | 840 |
| Плиты древесно-волокнистые и древесно-стружечные (ГОСТ 4598-74, ГОСТ 10632-77) | 200…1000 | 0.06…0.15 | 2300 |
| Плиты из керзмзито-бетона | 400…600 | 0.23 | — |
| Плиты из полистирол-бетона ГОСТ Р 51263-99 | 200…300 | 0.082 | — |
| Плиты из резольноформальдегидного пенопласта (ГОСТ 20916-75) | 40…100 | 0.038…0.047 | 1680 |
| Плиты из стеклянного штапельного волокна на синтетическом связующем (ГОСТ 10499-78) | 50 | 0.056 | 840 |
| Плиты из ячеистого бетона ГОСТ 5742-76 | 350…400 | 0.093…0.104 | — |
| Плиты камышитовые | 200…300 | 0.06…0.07 | 2300 |
| Плиты кремнезистые | 0.07 | — | |
| Плиты льнокостричные изоляционные | 250 | 0.054 | 2300 |
| Плиты минераловатные на битумной связке марки 200 ГОСТ 10140-80 | 150…200 | 0.058 | — |
| Плиты минераловатные на синтетическом связующем марки 200 ГОСТ 9573-96 | 225 | 0.054 | — |
| Плиты минераловатные на синтетической связке фирмы «Партек» (Финляндия) | 170…230 | 0.042…0.044 | — |
| Плиты минераловатные повышенной жесткости ГОСТ 22950-95 | 200 | 0.052 | 840 |
| Плиты минераловатные повышенной жесткости на органофосфатном связующем (ТУ 21-РСФСР-3-72-76) | 200 | 0.064 | 840 |
| Плиты минераловатные полужесткие на крахмальном связующем | 125…200 | 0.056…0.07 | 840 |
| Плиты минераловатные на синтетическом и битумном связующих | — | 0.048…0.091 | — |
| Плиты мягкие, полужесткие и жесткие минераловатные на синтетическом и битумном связующих (ГОСТ 9573-82, ГОСТ 10140-80, ГОСТ 12394-66) | 50…350 | 0.048…0.091 | 840 |
| Плиты пенопластовые на основе резольных фенолформальдегидных смол ГОСТ 20916-87 | 80…100 | 0.045 | — |
| Плиты пенополистирольные ГОСТ 15588-86 безпрессовые | 30…35 | 0.038 | — |
| Плиты пенополистирольные (экструзионные) ТУ 2244-001-47547616-00 | 32 | 0.029 | — |
| Плиты перлито-битумные ГОСТ 16136-80 | 300 | 0.087 | — |
| Плиты перлито-волокнистые | 150 | 0.05 | — |
| Плиты перлито-фосфогелевые ГОСТ 21500-76 | 250 | 0.076 | — |
| Плиты перлито-1 Пластбетонные ТУ 480-1-145-74 | 150 | 0.044 | — |
| Плиты перлитоцементные | — | 0.08 | — |
| Плиты строительный из пористого бетона | 500…800 | 0.22…0.29 | — |
| Плиты термобитумные теплоизоляционные | 200…300 | 0.065…0.075 | — |
| Плиты торфяные теплоизоляционные (ГОСТ 4861-74) | 200…300 | 0.052…0.064 | 2300 |
| Плиты фибролитовые (ГОСТ 8928-81) и арболит (ГОСТ 19222-84) на портландцементе | 300…800 | 0.07…0.16 | 2300 |
termoizol.com
1.5.Теплопроводность цилиндрической стенки (трубы)
Цилиндрические стенки встречаются часто, например, изолированный трубопровод представляет собой многослойную цилиндрическую стенку. Найдем тепловое сопротивление сначала однослойной трубы 1, разбив ее цилиндрическими поверхностями на бесконечно большое число слоев (рис. 1.8).
Количество тепла Q, проходящее через каждый слой, будет равно
Q = — λF(dt/dr) = -2πrλl(dt/dr)= — dt/dR, (1.31)
где тепловое сопротивление элементарного слоя
dR=dr/2πrλl. (1.32)
Общее тепловое сопротивление определим по формуле
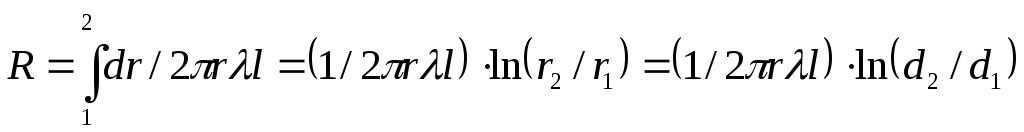 ,
(1.33)
,
(1.33)
где l и d — соответственно длина и диаметр трубы, м.
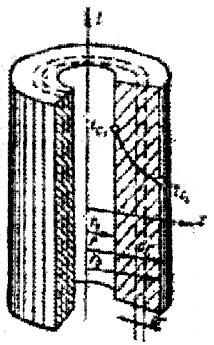
Рис 1.8. Теплопроводность однородной цилиндрической
стенки
Для многослойной трубы (рис. 1.9), например, стальной, покрытой слоем тепловой изоляции, формула (1.33) видоизменяется следующим образом:
 .
(1.34)
.
(1.34)
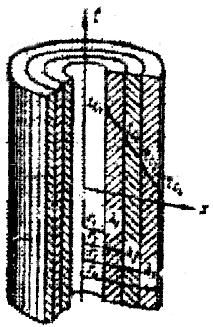
Рис. 1.9. Теплопроводность многослойной цилиндрической стенки
Количество тепла, проходящее через трубу в единицу времени
Q= q= (tc1 –tС2)/ R=2πλl∙((tc1 —tc2)/ln(d2/d1)), Вт. (1.35) (1-35)
Количество тепла, отнесенное к 1 м длины трубы
q= Q/l = 2πλ(Δt/ln(d2/d1)), Вт/м (1.36)
Количество тепла, отнесенное к 1 м2 внешней поверхности трубы
q1=Q/ πd21=2λΔt/d2In(d2/d1), Вт/м2. (1.37)
Температура внутри стенки для каждого слоя распределяется по логарифмической кривой, изображенной на рис. 1.9, в соответствии с формулой
tx=t1-(tc1 -tc2)/ln((d2/d1)∙In(dx/d1). (1.38) (1-38)
Экспериментальное определение коэффициента теплопроводности
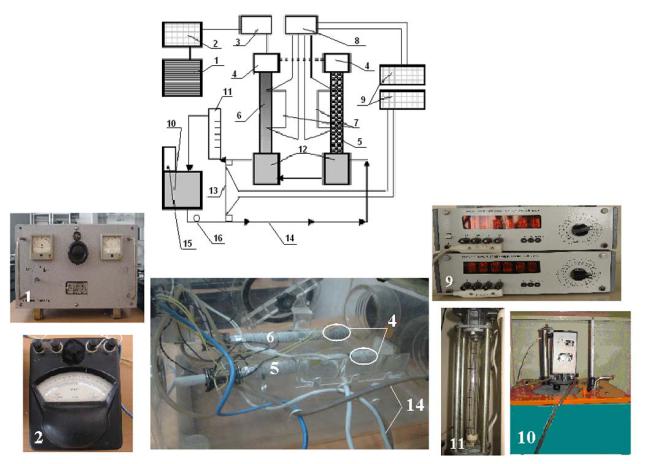
Можно опытным путем определять значения коэффициента теплопроводности λ для изоляционных материалов при невысоких температурах (до 300°С), пользуясь прибором, изображенным на схеме (рис. 1.10). Исследуемый материал помещают на наружной поверхности трубы длиной 1,5 м (чтобы избежать слияния торцов).
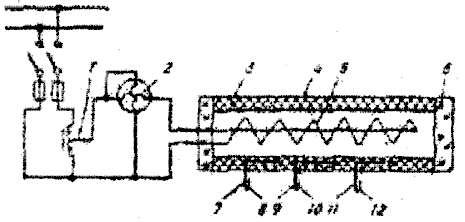
Рис. 1.10. Схема опытной установки:
1-автотрансформатор; 2-ваттметр; 3-труба; 4-исследуемый материал; 5-электроический нагреватель; 6-тепловая изоляция; 7-12-термопары.
Внутри трубы 4 заложен электрический нагреватель, мощность которого измеряется ваттметром 2. Температуры материала измеряются термопарами 7—12, горячие спаи которых заложены на наружной и внутренней поверхностях материала. Коэффициент теплопроводности определяют по формуле
λ=Q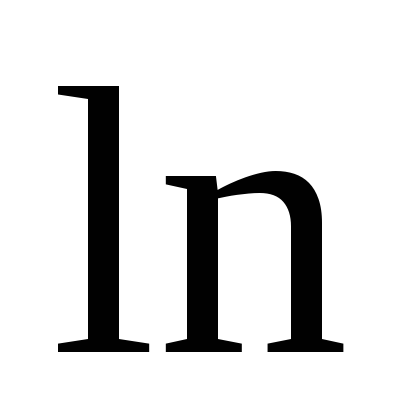 (d2/d1)/2πl (tc1 –tc2),
Вт/(м·град).
(1.39)
(d2/d1)/2πl (tc1 –tc2),
Вт/(м·град).
(1.39)
1.6.Теплопроводность при нестационарном тепловом
режиме
Нагревание или охлаждение тел явление очень распространенное в производственных установках (например, нагревание стальных слитков в промышленных печах, охлаждение нагретых предметов на воздухе и т. д.).
При этом температурное поле тела изменяется во времени, что обусловливается изменением энтальпии тела и является при-
знаком нестационарного теплового режима.
При нагревании тела тепло, воспринимаемое внешней его поверхностью от окружающего пространства печи, постепенно проникает внутрь материала вследствие его теплопроводности и разности температур поверхности и внутренних слоев материала. Для простоты рассмотрим случай нагрева неограниченной пластины (рис. 1.11), когда плотность теплового потока движется только в направлении оси х (перпендикулярно к поверхности пластины).
Нестационарный процесс нагрева описывается уравнением Фурье (1.18). ∂t/∂τ =a(∂2t/∂x2), (1.40) (1-40)
где a — коэффициент температуропроводности, м2/с.
Если среда, окружающая тело, имеет температуру tокp, то по формуле (1.20) можно написать уравнение
α(tокр — tnoв)= -λ(∂t/∂x)пов,
где α — коэффициент теплоотдачи от окружающей среды к поверхности тела.
Само собой разумеется, что на распределение температур в теле влияют толщина пластины s (при двустороннем нагреве удобно толщину пластины принимать за 2s) и начальная температура тела to. Следовательно, температура каждой точки тела описывается уравнением, имеющим вид
t= f (х,τ,а,λ,α,tокр,t0,s). (1.41)
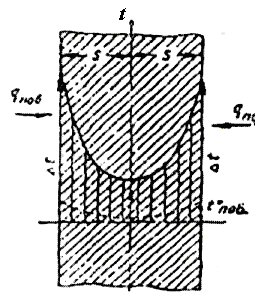
Рис. 1.11. К расчетам двустороннего симметричного
прогрева плиты
Большое число переменных затрудняет аналитическое решение такого уравнения. Задача легче решается, когда размерные переменные объединяются в безразмерные комплексы (критерии). Если переменная выражается в долях от другой одноименной величины, принимаемой за характерную, то безразмерная величина, называемая симплексом, характеризует или то, насколько она отличается от максимальной (например, безразмерная температура θ=t/tmax ≤1), или во сколько раз она превышает величину, принятую в качестве калибра (например, безразмерная длина трубы L= 1/d кратна ее диаметру). Безразмерные комплексы или критерии подобия состоят из разноименных величин, объединение которых осуществляется строго по соответствующим правилам.
studfile.net
03 Теплопроводность металлов и тепловой трубы
Лабораторная работа № 3
ИЗМЕРЕНИЕ И СРАВНЕНИЕ КОЭФФИЦИЕНТОВ ТЕПЛОПРОВОДНОСТИ МЕТАЛЛОВ И ТЕПЛОВОЙ ТРУБЫ
Согласно термодинамике, изолированная (или замкнутая) система с течением времени приходит в термодинамическое равновесие. Например, при неоднородном распределении температуры в такой системе начнутся процессы передачи энергии от более нагретых частей системы к менее нагретым, т.е. возникнут потоки вещества и теплоты, выравнивающие температуру во всех частях системы.
Еслисистеманеявляетсяизолированной, т.е. можетобмениватьсявеществомиэнергиейсокружающимителами (такие системы еще называют открытыми), то в ней также возникают потоки, стремящиеся выровнять температуру. Но из-за обмена энергией (и веществом) с другими телами эта система не придет в термодинамическое равновесие. С течением времени в ней установятся стационарные (не меняющиеся со временем) потоки вещества и теплоты, а также стационарные распределения температуры и других макроскопических параметров (давления, плотности и т.д.).
Таким образом, при наличии температурных неоднородностей всегда возникают потоки тепла, т.е. происходит теплопередача. Можно выделить три вида теплопередачи: излучение, когда нагретое тело является источником электромагнитных волн; конвекция, когда энергия переносится макроскопическими потоками вещества; теплопроводность, когда перенос тепла происходит за счет хаотических движений отдельных частиц вещества — в более нагретых частях тела средняя кинетическая энергия частиц больше, чем в менее нагретых, и при взаимодействии частицы обмениваются энергией.
Вметаллах основным является электронный механизм теплопроводности — передача энергии при взаимодействии свободных электронов, которые можно уподобить идеальному одноатомному газу. В кристаллических твердых телах, где тепловые движения частиц имеют характер малых колебаний, теплопроводность обусловлена передачей энергии этих колебаний. В квантовой теории колебаниям сопоставляются особые фиктивные частицы (квазичастицы) — фононы. В металлах, наряду с основным электронным, действует также фононный механизм теплопроводности, хотя при обычных и высоких температурах доля его не велика.
Знание теплопроводности необходимо для расчета различных физических и технических приборов и установок. Для физической науки явление теплопроводности металлов особенно важно потому, что в нем одновременно участвуют и ионная, и электронная системы (ионная система образует кристаллическую решетку) твердого тела.
Впоследнее время возникла необходимость в создании мощных и эффективных теплопередающих устройств для аэрокосмической техники, радио — электронной аппаратуры, ядерных энергетических установок и т.д. Такие устройства были предложены в патенте Гровера в 1963 г. в Лос-Аламосской лаборатории (штат Нью-Мексико, США) и получили название тепловые трубы.
Тепловая труба — устройство, служащее для передачи теплоты. Тепловые трубы обладают высокой эффективной теплопроводностью, т.е. они способны передавать тепловые потоки высокой плотности при незначительных перепадах температуры между источником и стоком тепла. Перенос теплоты осуществляется в результате процессов испарения и конденсации теплоносителя, т.е. в результате конвекции теплоносителя в паровой и жидкой фазе во внутренней полости тепловой трубы.
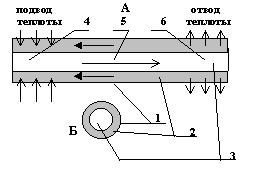
Тепловая труба имеет герметичный корпус (рис. 1), внутренняя поверхность которого покрыта капиллярной структурой — фитилем. Фитиль пропитан жидким теплоносителем, все остальное внутреннее пространство заполнено паром.
Рис. 1. Тепловая труба:
А — продольное сечение; Б — поперечное сечение; 1 — герметичный корпус трубы; 2 — капиллярная структура; 3- паровое пространство; 4 — испарительный участок; 5 — адиабатный участок; 6 — участок конденсации
Пусть один конец тепловой трубы расположен в более горячей зоне (подвод теплоты), а другой — в более холодной (отвод теплоты). Подвод и отвод теплоты находятся на некотором расстоянии друг от друга, и между ними расположен адиабатный участок (т.е. теплоизолированный, без теплообмена с внешней средой). В зоне подвода теплоты тепло передается через стенку корпуса и капиллярную структуру (фитиль), с поверхности которой испаряется жидкий теплоноситель, забирая скрытую теплоту фазового превращения жидкость — пар (теплота фазовых превра-
1
щений очень велика, например, при превращении 1 кг воды в пар поглощается около 2 миллионов Дж.). Об-
разующийся пар проходит адиабатный участок и конденсируется в зоне отвода тепла на поверхности фитиля. Выделяющаяся при конденсации теплота фазового превращения пар — жидкость отводится через слой фитиля и стенку корпуса. Из зоны конденсации в зону испарения жидкость возвращается по фитилю.
Таким образом, внутри тепловой трубы осуществляется замкнутая циркуляция (конвекция) теплоносителя с фазовыми превращениями жидкость — пар в зоне подвода тепла и пар — жидкость в зоне отвода тепла. Пар движется по паровомуканалувнаправлениикзонесменьшейтемпературой(зонеконденсации), ажидкостьпофитилювобратном направлении за счет капиллярных сил, т.е. поддерживается циркуляция действием капиллярных сил. Рассмотрим механизм, обеспечивающий циркуляцию теплоносителя.
Известно, что под действием разности давлений в жидкой Pж и паровой Pп фазах поверхность раздела фаз
искривляется и возникает явление поверхностного натяжения. Радиус искривленной поверхности — мениска — описывается уравнением Лапласа
Pσ = PП −PЖ = 2σ(1/ rи −1/ rк),
где rи и rк — радиусы кривизны менисков в зонах испарения и конденсации; σ — коэффициент поверхностного натяжения. В зоне испарения мениск имеет вогнутую форму, в зоне конденсации кривизна мениска незначительна и ею можно пренебречь.
Для устойчивой циркуляции теплоносителя движущий напор, создаваемый капиллярным давлением, должен превосходить перепад давления по длине контура циркуляции:
Pσ ≥ PП + PЖ.
Здесь Pп, Pж — перепадыдавлениявпаровойижидкойфаземеждуповерхностямииспаренияиконденсации.
Равенство в этой формуле будет означать то, что радиус испаряющего мениска становится равен эффективному (среднему) размеру пор фитиля и тепловая труба при этом передает максимальный тепловой поток.
Таким образом, в тепловой трубе реализованы два наиболее важных физических явления, широко, впрочем, используемых в природе, — капиллярные явления и фазовые превращения.
1. Основы метода измерения коэффициента теплопроводности
Количественно явление теплопроводности описывается законом Фурье. Если температура меняется от точки к точке, то говорят, что имеется градиент температуры (он равен изменению температуры на единицу длины и указывает направление, в котором наиболее сильно возрастает температура). Количество энергии (тепла), передаваемое за единицу времени через поверхность, перпендикулярную градиенту температуры, называется тепловым потоком Q (Вт). Отнесение этого потока к единице выбранной поверхности называют плотностью теплового потока q (Вт/м2).
Математический закон теплопроводности — закон Фурье — выражается формулой
Знак минус в равенстве (1.1) означает, что теплота переносится в сторону убывания температуры. Если градиент температуры направлен вдоль оси X, то закон Фурье может быть представлен в виде
qx = −λ dT | = −λ xT . | (1.2) | ||
dx |
|
|
| |
Если градиент температуры одинаков во всех точках тела, а поток тепла стационарный (не изменяющийся со | ||||
временем), то формулу (1.2) можно переписать в виде | T1 |
|
| |
Q = λ | S , | (1.3) | ||
| ||||
| l |
| ||
где Т1- разность температур между двумя сечениями тела S, расстояние между которыми l.
Коэффициент теплопроводности λ численно равен плотности теплового потока при единичном градиенте
температуры.
Измерить теплопроводность вещества — значит измерить его коэффициент теплопроводности. Из (1.3) следует, что коэффициент теплопроводности вычисляется по формуле
λ = | Ql | . | (1.4) |
| |||
| S T |
| |
| 1 |
|
|
Таким образом, для определения коэффициента теплопроводности нужно измерить количество теплоты, передаваемое через сечение тела в единицу времени (тепловой поток) Q, площадь этого сечения S, разность температур T1 и расстояние l между двумя выбранными сечениями.
Так как в металлах носителями тепловой и электрической энергии являются электроны, то коэффициенты теплопроводности и электропроводности пропорциональны друг другу. При повышении температуры вследствие усиления тепловых неоднородностей рассеяние электронов увеличивается. Это влечет за собой уменьшение коэффициентов тепло- и электропроводности чистых металлов с ростом температуры.
При наличии разного рода примесей коэффициент теплопроводности металлов резко убывает. Это можно объяснить увеличением структурных неоднородностей, которые приводят к рассеянию электронов. Так, например, для чистой меди λ=396 Вт/м К, а для меди со следами мышьяка λ=142 Вт/м К.
В отличие от чистых металлов коэффициенты теплопроводности сплавов при повышении температуры увеличиваются.
2. Описание экспериментальной установки
Принципиальная схема установки для определения коэффициента теплопроводности металлов (твердых тел) представлена на рис.2.
Рис. 2. Схема и фото экспериментальной установки:
1 — блок питания; 2 — ваттметр; 3 — переключатель нагревателей; 4 — подвод теплоты; 5 — тепловая труба; 6 — медный стержень; 7 — дифференциальные термопары на образцах; 8 — переключатель термопар; 9 — милливольтметры; 10 — термостат; 11 — расходомер; 12 — отвод теплоты; 13 — дифференциальная термопара; 14 — магистраль охлаждения; 15 — регулятор термостата; 16 — зажим
В боксе помещены два исследуемых образца: медный стержень и тепловая труба. На одном конце каждого из образцов помещен электрический нагреватель, мощность которого задается блоком питания и контролируется по ваттметру. Переключатель нагревателей «НАГРЕВ» (расположен на стенке бокса) имеет три положения: «медный стержень», «тепловая труба» и «выключено».
Охлаждение образцов осуществляется циркулирующей по линии охлаждения водой. Постоянство расхода воды (а значит, и отводимого от образца теплового потока) может быть достигнуто с помощью регулятора термостата и зажима на линии охлаждения.
Массовый расход воды m& измеряется расходомером с ценой деления 0,5 г/с. Если разность температур холод-
ной (на выходе из термостата) и нагретой образцом воды T2 известна (измеряется дифференциальной термопарой), то тепловой поток Q может быть рассчитан по формуле
где с = 4.2 Дж/г К — удельная теплоемкость воды.
Поскольку площадь S сечения цилиндрического образца равна S=πd2 /4, где d — диаметр цилиндра, то формулу (1.4) с учетом (2.1) можно представить в виде
& | T2l |
|
| |
λ = 4 | mc | . | (2.2) | |
πd2 |
| |||
| T |
| ||
|
| 1 |
|
|

Разность температур Т1 (вдоль образцов) измеряется дифференциальными термопарами. Переключатель термопар»Дифференциальнаятермопара» имеетдваположения: «медныйстержень» и»тепловаятруба». Расстояниямежду спаями термопар l одинаковы для обоих образцов (l = 15 10-2 м). Одинаковы и диаметры образцов (d = 1,6 10-2 м).
Милливольтметры измеряют термо — ЭДС дифференциальных термопар E (mV). Поскольку связь между разностью температур и термо – ЭДС линейна, то очевидно, что в формулу (2.2) вместо разности температур можно подставлять соответствующее значение термо-ЭДС в mV.
3. Методика проведения эксперимента
П о д г о т о в к а к о п ы т у
Ознакомиться с описанием и лабораторной установкой.
Внимание! Питание блока питания, термостата и милливольтметров осуществляется напряжением 220 В, соблюдайте осторожность при работе! Помните, что тепловая труба представляет собой двухфазную систему (жидкость — пар) и при отсутствии охлаждения ее конденсатора взрывоопасна. Поэтому необходимо вначале включить термо-
стат и убедиться по расходомеру (расход воды должен быть не ниже 5 г/с) в наличии расхода охлаждающей конденсатор воды.
З а д а н и е
В настоящей работе необходимо измерить коэффициент теплопроводности медного стержня и тепловой трубы. Сравнить их теплопроводности и убедиться в том, что тепловая труба является сверхпроводником тепла.
1.Включить термостат и установить (с помощью регулятора термостата и зажима) по расходомеру массовый расход воды на отметке 10 (по верхней части поплавка расходомера), что соответствует 5 г/c.
2.Включить приборы для измерения термо — ЭДС термопар и дождаться установления стационарных условий, т.е. неизменности показаний приборов (значения могут меняться в последнем знаке после запятой, колеблясь вблизи
некоторого значения). При этом, работая с тепловой трубой, установить предел измерения T1 на милливольтметре 1 мВ, а предел измерения T2 — 10 мВ. При работе с медным стержнем эти же пределы устанавливаются наоборот. После установления стационарных условий списать показания приборов и считать их начальными.
3.Поставить переключатели «нагрев» и «дифференциальная термопара» в положение «тепловая труба».
4.Включить блок питания и установить 20 Вт по ваттметру, предварительно определив его цену деления. Сле-
дить за показаниями милливольтметров. При нормальной работе тепловой трубы показания T2 должны быть зна-
чительно больше начальных и не уменьшаться (если это не так, то срочно выключить блок питания и пригласить преподавателя). Дождаться неизменности показаний милливольтметров и снять эти показания.
5.Проделать то же самое при показаниях ваттметра 30, 40, 50 Вт.
6.Выключить блок питания, установив сначала показания ваттметра на нуль, а затем поставить переключатель «нагрев» в положение «выключено». Дождаться неизменности показаний милливольтметров и списать эти показания.
7.Поставить переключатели «нагрев» и «дифференциальная термопара» в положение «медный стержень». Установить 10 Вт по ваттметру, дождаться неизменности показаний милливольтметров и списать эти показания. Проделать то же для 15 и 20 Вт. После этого выключить все приборы.
8. Вычислить T1, T2 с учетом их начальных значений и рассчитать соответствующие значения коэффици-
ентов теплопроводности.
Данные измерений и вычислений занести в таблицу.
Экспериментальные данные
| N, | T1, | T2 , | m , | λ , |
|
|
| & |
| |
| Вт | мВ | мВ | г/с | Вт/м К |
Тепловая |
|
|
|
|
|
труба |
|
|
|
|
|
Медный |
|
|
|
|
|
стержень |
|
|
|
|
|
Относительная систематическая погрешность определения λ для доверительной вероятности P=0,95 равна
λ = |
| & |
| 2 |
| ( T1) | 2 |
| ( T2 ) |
| 2 | (3.1) |
m |
| + |
| + |
| . | ||||||
λ |
| m |
|
|
|
|
|
|
|
|
|
|
|
|
|
| T1 |
| T2 |
|
| ||||
|
| & |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
9.Рассчитать систематическую (по последним измерениям) и случайную погрешности определения λ тепловой трубы и медного стержня.
10.Сделать выводы.
4.Контрольные вопросы
1.В чем состоит явление теплопроводности?
2.Каков физический смысл коэффициента теплопроводности?
3.Каков физический смысл градиента температуры? Как направлен вектор градиента? Как направлен вектор потока тепла?
4.В каких единицах измеряется коэффициент теплопроводности?
5.Что такое поток тепла? Что такое плотность потока тепла?
6.Каков физический смысл теплопроводности металлов?
7.Как зависит теплопроводность чистых металлов от температуры? Каковы численные значения (по порядку величины) коэффициентов теплопроводности металлов?
8.Как устроена и работает тепловая труба?
9.Какие известные Вам физические явления использованы в работе тепловой трубы? Сформулируйте условия работоспособности тепловой трубы.
Список литературы
1.Кикоин А.К., Кикоин И.К. Молекулярная физика. М.: Наука, 1976.
2.Дан П., Рей Д. Тепловые трубы. М.: Энергия, 1979.
3. Преображенский В.П. Теплотехнические измерения и приборы. М.: Энергия, 1978.
4. Енохович А.С. Краткий справочник по физике. М.: Высш. шк.,1976.
studfile.net
Теплопроводность стенки трубы — Энциклопедия по машиностроению XXL
Задача 13.2. Паропровод диаметром djd.2 = 150/160 мм покрыт слоем теп-.ювой изоляции толщиной б = 100 мм коэффициент теплопроводности стенки трубы = 50 Вт/(м К), а изоляции = 0,08 Вт/(м К). Температура внутренней поверхности паропровода = 400 °С, наружной поверхности изоляции [c.175]X — теплопроводность стенки трубы. [c.300]
Полное решение задачи для произвольно задаваемого распределения плотности теплового потока по окружности трубы требует составления довольно обширных таблиц. Однако решение для простого косинусоидального распределения плотности теплового потока по окружности трубы можно записать в очень компактном виде. Так как теплопроводность стенки трубы до некоторой степени сглаживает изменение температуры по окружности, распределение плотности теплового потока по окружности во многих прикладных задачах можно аппроксимировать косинусоидальной зависимостью. [c.212]
Ям —коэффициент теплопроводности стенки трубы, вт м град-, [c.215]
Термическое сопротивление оксидной пленки, м К/Вт Теплопроводность стенок труб греющей секции, Вт/(м К) [c.290]
Теплопроводность стенки трубы 249 [c.249]
Теплопроводность стенки трубы 251 [c.251]
По табл. 2-1 находим коэффициенты теплопроводности стенки трубы >.0 = 50 ккал/м час град, первого слоя изоляции Г, = 0,12 час и второго слоя [c.104]
Трубчатый воздушный подогреватель производительностью 2,78 кг воздуха в 1 с выполнен из труб диаметром й(/йз = 43/49 мм. Коэффициент теплопроводности материала труб Л=50 Вт/(м °С). Внутри труб движется горячий газ, а наружная поверхность труб омывается поперечным потоком воздуха. Средняя температура дымовых газов /ц(1 = 250°С, а средняя температура подогреваемого воздуха 1к2=145°С. Разность температур воздуха на входе и выходе из подогревателя равна 6 =250° С. Коэффициент теплоотдачи от газов к стенке ai = 45 Вт/(м — С) и от стенки к воздуху 03 = =25 Вт/(м2.°С), [c.18]
Температура у основания ребра о = 80°С температура окружающего воздуха f)K=18° . Коэффициент теплоотдачи от ребер и внешней поверхности трубы к окружающему воздуху а = 9,3 Вт/ /(м -°С) коэффициент теплопроводности стенки Л=55,7 Вт/(м-°С), [c.22]
Определение коэффициента теплопроводности теплоизоляционных материалов методом трубы. Метод трубы основан на законе теплопроводности цилиндрической стенки. Схема прибора представлена на рис. 32-1. На медную трубу 2 с наружным диаметром di и длиной I накладывается цилиндрический слой исследуемого материала с диаметром d.2, внутри трубы заложен электрический нагреватель 3, создающий равномерный ее обогрев. Равномерность обогрева изоляции 1 обеспечивается] хорошей теплопроводное медной трубы. Сила тока в нагревателе регулируется реостатом. Теплота Q, выделяемая нагревателем 3, определяется по мощности тока, измеряемой амперметром и вольтметром. [c.519]
Уравнение (25.7)—уравнение энергии для движущейся в трубе жидкости. Уравнение (25.8) —уравнение теплопроводности для стенки трубы. [c.299]
Теплопроводность углеродистой стали 30 при = 100°С .2 = 50,2 Вт/(м-К). Температура наружной стенки трубы [c.434]
Теплопроводность углеродистой стали при = 100 Л,=50,2 Вт/(м-К). Толщина стенки трубы [c.436]
Рассмотрим стационарный процесс теплопроводности через однородную цилиндрическую стенку (трубу) длиной I с внутренним радиусом Г] и наружным Г2 (рис. 13.3). Теплопроводность материала стенки Л — величина постоянная. На поверхности стенки заданы постоянные температуры и t 2 [c.292]
Паропровод диаметром 150/160 мм покрыт с.ноем тепловой изоляции толщиной биа=100 ММ коэффициенты теплопроводности стенки трубы . = 50 Вт/(м-°С) н изоляции >.2 = 0,08 Вт/(м-°С). Температура на впутреиней поверхности паропровода [c.14]
Подняв и (приблизив значение меньшего 1Коэффиц и-ента теплоотдачи к (большему, (следует использовать возможность (повышения (отношения l/s, т. е. всемер(Ного уменьшения термического сопротивления, обусловленного малой теплопроводностью стенки трубы (это имеет место при (неметаллических Т(рубах) и гла(вное загрязнениями из на(К ши, нагарш и отложений всех видов. [c.304]
При расчете теплообмена конвективных поверхностей нагрева используют коэффициент теплопередачи, который для многослойной стенки, какой является труба котла с наружными и внутренними загрязненями, зависит от коэффициента теплоотдачи от газов к стенке трубы и от трубы к нагреваемой среде, а также от толщины и теплопроводности стенки трубы и наружных и внутреншх отложений. [c.52]
В которой под q следует понимать количество тепла, проходящее через основание плавника Я,тр — коэффициент теплопроводности стенки трубы в основании трубы 11пл—коэффициент растечки под плавником. [c.103]
Крашенинников В. В. О допустимости замены уравнения теплопроводности стенки трубы уравнением баланса тепла при исследовании переходных процессов в теплообменниках. — В кн. Доклады П1 конференции НТОЭ и ЭП при ВТИ им. Дзержинского. М., ОНТИ ВТИ, 1970. [c.412]
Д.— Т. э. был обнаружен и исследован англ. учёными Дж. П. Джоулем и У, Томсоном (Кельвином) в 1852—62. В опытах Джоуля и Томсона измерялась темп-ра в двух последоват. сечениях непрерывного и стационарного потока газа (до дросселя и за ним). Вследствие значит, трения газа в дросселе (мелкопористой пробке из ваты) скорость газового потока была очень малой и кинетич. энергия потока при дросселировании практически не изменялась. Благодаря низкой теплопроводности стенок трубы и дросселя теплообмен между газом и внеш. средой отсутствовал. При перепаде давления на дросселе Ap=pi— —Ра равном атм. давлению, измеренная разность темп-р АТ—Т —Т для воздуха составила —0,25°С (опыт проводился при комнатной темп-ре). Для СО2 и На в тех же условиях АТ оказалась соотв. равной —1,25 и -f-0,02° , Д,— Т. э, принято называть положительным, если газ в процессе дросселирования охлаждается (ЛГ 0). [c.154]
Фултона [18], Шспера [19] и Ван-Демтсра [20] ). Строгое теоретическое рассмотрение сложного турбулентного течения газа, которое имеет место в вихревой трубе, является чрезвычайно трудной задачей, особенно в связи с тем, что профиль скоростей потока внутри трубы экспериментально пока еще не определен. Однако качественно эффект охлаждения можно объяснить следую-п им образом. Вращающийся поток воздуха внутри трубы создает в радиальном направлении градиент давления, возрастающий от оси к стенке трубы. Влияние турбулентности на такое ноле давлений выражается в адиабатическом перемешивании. Это приводит к созданию адиабатического распределения температур, при котором более холодный газ оказывается в области, расположенной вблизи оси трубы. Однако вследствие теплопроводности, приводящей к уменьшению градиента температур в радиальном направлении а также непостоянства значений угловой скорости в разных местах трубы адиабатическое распределение полностью осуществлено быть не может. Ван-Демтор описывает последний эффект следующим образом Если угловая скорость непостоянна, то вступает п действие другой механизм, приводящий к возникновению потока механической энергии в радиальном направлении наружу. Вследствие турбулентного трения (вихревой вязкости) внутренние слои жидкости или газа стремятся заставить внешние слои двигаться с той [c.13]
Рассмотрим однослойную цилпидрическую стенку (трубу) с внутренним д 1аметром с/,,,,, наружным и длиной I. Стенка трубы характеризуется коэффициентом теплопроводности X. Внутри трубы течет более нагретая среда с температурой /т, снаружи — более холодная с температурой t . Суммарные коэффициенты теплоотдачи на внутренней и наружной поверхностях трубы j,H и н. Температуры г.оверхностей стенки и t -i неизвестны фис. 19.2). [c.230]
Вычислить потерю теплоты с 1м неизолированного трубопровода диаметром б1/(12=150/165мм, проложенного на открытом воздухе, если внутри трубы протекает вода со средней температурой 1ж1=90°С и температура окружающего воздуха 1 2= -15°С. Коэффициент теплопроводности материала трубы Х=50 Вт/(м °С), Коэффициент теплоотдачи от воды к стенке трубы 1=1000 Вт/(м °С) и от трубы к окружающему воздуху 2=12 Вт/(м -°С). Определить так же темпере-туры на внутренней и внешней поверхностях трубы, [c.29]
ТОЛЩИНА СТЕНКИ ТРУБЫ, М=.0015 7 КОЭФ.ТЕПЛОПРОВОДНОСТИ СТЕНКИ =45 ВВЕДИТЕ ТЕПЛОЕМКОСТЬ, ПЛОТНОСТЬ, ТЕПЛОПРОВОДНОСТЬ И ЧИСЛО ПРАНДТЛЙ ТЕПЛОНОСИТЕЛЯ-1 ПРИ ТЕМПЕРАТУРЕ (Т1ВХ+Т1ВЫХ)/2= 72.5 [c.293]
mash-xxl.info
