В чем измеряется теплота: Теплота сгорания — Википедия – величина, принципы расчетов, порядок вычислений

Количество теплоты. Единицы количества теплоты. Видеоурок. Физика 8 Класс

В данном уроке рассматривается понятие количества теплоты.

Если до этого момента мы рассматривали общие свойства и явления, связанные с теплом, энергией или их передачей, то теперь пришло время познакомиться с количественными характеристиками этих понятий. А точнее, ввести понятие количества теплоты. На этом понятии будут основаны все дальнейшие расчеты, связанные с преобразованиями энергии и теплотой.

          Определение

Количество теплоты – это энергия, которая передается с помощью теплопередачи.

 

Рассмотрим вопрос: какой величиной мы будем выражать это количество теплоты?

Количество теплоты связано с внутренней энергией тела, поэтому, когда тело получает энергию, его внутренняя энергия увеличивается, а когда отдает – уменьшается (рис. 1).

Рис. 1. Взаимосвязь количества теплоты и внутренней энергии

Аналогичные выводы можно сделать и о температуре тела (рис. 2).

Рис. 2. Взаимосвязь количества теплоты и температуры

          Внутренняя энергия выражается в джоулях (Дж). Значит, количество теплоты также измеряется в джоулях (в СИ):

.

 

 – стандартное обозначение количества теплоты.

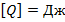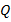
Чтобы выяснить: от чего зависит 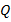, проведем 3 эксперимента.

 

Эксперимент № 1

Возьмем два одинаковых тела, но разной массы. Например, возьмем две одинаковые кастрюли и нальем в них разное количество воды (одинаковой температуры).

Очевидно, что для того, чтобы вскипятить ту кастрюлю, в которой воды больше, потребуется больше времени. То есть ей необходимо будет сообщить большее количество теплоты.

Из этого можно сделать вывод, что количество теплоты зависит от массы (прямо пропорционально – чем больше масса, тем больше количество теплоты).

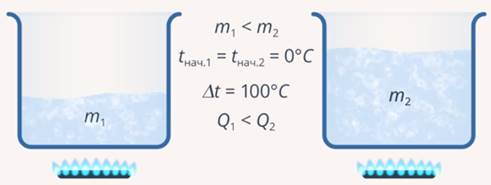
Рис. 3. Эксперимент № 1

Эксперимент № 2

Во втором эксперименте мы будем нагревать тела одинаковой массы до разной температуры. То есть возьмем две кастрюли с водой одинаковой массы и нагреем одну из них на 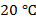, а вторую, к примеру, на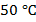

.

Очевидно, что, для того чтобы нагреть кастрюлю до большей температуры, понадобится больше времени, то есть ей необходимо будет сообщить большее количество теплоты.

Из этого можно сделать вывод, что количество теплоты зависит от разности температур (прямо пропорционально – чем больше разность температур, тем больше количество теплоты).

Рис. 4. Эксперимент № 2

Эксперимент № 3

В третьем эксперименте рассмотрим зависимость количества теплоты от характеристик вещества. Для этого возьмем две кастрюли и нальем в одну из них воду, а в другую – подсолнечное масло. При этом температуры и массы воды и масла должны быть одинаковы. Будем нагревать обе кастрюли до одинаковой температуры. 

Для того чтобы нагреть кастрюлю с водой, потребуется больше времени, то есть ей необходимо будет сообщить большее количество теплоты.

Из этого можно сделать вывод, что количество теплоты зависит от рода вещества (подробнее о том, как именно, мы поговорим на следующем уроке).

Рис. 5. Эксперимент № 3

          После проведенных экспериментов можно сделать вывод, что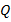

 зависит:

• от массы тела;
• изменения его температуры;
• рода вещества.

Отметим, что во всех рассмотренных нами случаях речь не идет о фазовых переходах (то есть изменениях агрегатного состояния вещества).

Вместе с тем численное значение количества теплоты может зависеть и от его единиц измерения. Кроме джоуля, который является единицей СИ, используется еще одна единица измерения количества теплоты – калория (переводится как «жар», «тепло»).

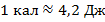
Это достаточно маленькое значение, поэтому чаще используется понятие килокалории: 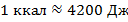. Эта величина соответствует количеству теплоты, которое необходимо передать  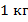воды, чтобы нагреть его на .

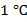На следующем уроке мы рассмотрим понятие удельной теплоемкости, которая связывает вещество и количество теплоты.

         

Список литературы

1. Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
2. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
3. Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «festival.1september.ru» (Источник)
2. Интернет-портал «class-fizika.narod.ru» (Источник)
3. Интернет-портал «school.xvatit.com» (Источник)

 

Домашнее задание

1. Стр. 20, параграф 7, вопросы № 1–6. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
2. Почему вода в озере остывает за ночь гораздо меньше, чем песок на пляже?
3. Почему климат, для которого характерны резкие перепады температуры между днем и ночью, называют резко континентальным?

Единица измерения количества теплоты, теория и онлайн калькуляторы

Определение

Количеством теплоты или просто теплотой ($Q$) называют внутреннюю энергию, которая без совершения работы передается от тел с более высокой температурой к телам с более низкой температурой в процессах теплопроводности или лучеиспускания.

Джоуль — единица измерения количества теплоты в системе СИ

Единицу количества теплоты можно получить из первого начала термодинамики:

\[\Delta Q=A+\Delta U\ \left(1\right),\]

где $A$ — работа термодинамической системы; $\Delta U$ — изменение внутренней энергии системы; $\Delta Q$ — количество теплоты, подводимое к системе.

Из закона (1), а тем более из его варианта для изотермического процесса:

\[\Delta Q=A\ \left(2\right).\]

очевидно, что в Международной системе единиц (СИ) джоуль (Дж) — единица измерения энергии и работы.

Через основные единицы джоуль легко выразить, если использовать определение энергии ($E$) вида:

\[E=mc^2\left(2\right),\]

где $c$ — скорость света; $m$ — масса тела. Исходя из выражения (2), имеем:

\[\left[Q\right]=\left[E\right]=кг\cdot {\left(\frac{м}{с}\right)}^2=\frac{кг\cdot м^2}{с^2}.\]

С джоулем используют все стандартные приставки системы СИ, обозначающие десятичные дольные и кратные единицы. Например, $1кДж={10}^3Дж$; 1МДж =${10}^6Дж$; 1 ГДж=${10}^9Дж$.

Эрг — единица измерения количества теплоты в системе СГС

В системе СГС (сантиметр, грамм, секунда) теплота измеряется в эргах (эрг). При этом одни эрг равен:

\[1\ эрг=1\ дин\cdot 1\ см.\]

Принимая во внимание то, что:

\[1\ Н={10}^5{\rm дин};;1\ {\rm м}=100\ см,\]

получаем соотношение между джоулем и эргом:

\[1\ Дж={10}^7эрг.\]

Калория — единица измерения количества теплоты

В качестве внесистемной единицы измерения количества теплоты используется калория. Одна калория равна количеству теплоты, которое следует передать воде массой один килограмм, чтобы нагреть ее на один градус Цельсия. Соотношение между джоулем и калорией следующее:

\[1кал\approx 4,2\ Дж.\]

Если говорить точнее, то различают:

• Международную калорию, она равна:
\[1\ кал=4,1868\ Дж;;\]
• термохимическую калорию:
\[1\ кал=4,184\ Дж;;\]
• 15-градусная калория, используемая для термических измерений:
\[1\ кал=4,1855\ Дж;;\]

Часто калории используют с десятичными приставками, такими как: ккал (килокалория) $1ккал={10}^3кал$; Мкал (мегакалория) 1Мкал =${10}^6кал$; Гкал (гигакалория) 1 Гкал=${10}^9кал$.

Иногда килокалорию называют большой калорией или килограмм-калорией.

Примеры задач с решением

Пример 1

Задание. Какое количество теплоты поглощает водород массой $m=0,2$кг при его нагревании от $t_1=0{\rm{}^\circ\!C}$ до $t_2=100{\rm{}^\circ\!C}$ при неизменном давлении? Запишите ответ в килоджоуля

Тепловой эффект химической реакции — Википедия

Тепловой эффект химической реакции — изменение внутренней энергии ΔU{\displaystyle \Delta U} или энтальпии ΔH{\displaystyle \Delta H} системы вследствие протекания химической реакции и превращения исходных веществ (реактантов) в продукты реакции в количествах, соответствующих уравнению химической реакции (стехиометрии реакции^[1]) при следующих условиях:

• единственно возможной работой при этом является работа против внешнего давления,
• как исходные вещества, так и продукты реакции имеют одинаковую температуру^[2][3].

Теплота термохимического процесса и тепловой эффект химической реакции[править | править код]

Поясним приведённое выше определение теплового эффекта химической реакции^{[K 1]}. Для этого запишем фундаментальные уравнения Гиббса для внутренней энергии и энтальпии простой^[10]открытой однородной термодинамической системы^[11][12]:

dU=TdS−PdV+∑i=1kμidni,{\displaystyle dU=TdS-PdV+\sum _{i=1}^{k}\mu _{i}dn_{i},}

(Фундаментальное уравнение Гиббса для внутренней энергии)

dH=TdS+VdP+∑i=1kμidni.{\displaystyle dH=TdS+VdP+\sum _{i=1}^{k}\mu _{i}dn_{i}.}

(Фундаментальное уравнение Гиббса для энтальпии)

Здесь T{\displaystyle T} — абсолютная температура, S{\displaystyle S} — энтропия, P{\displaystyle P} — давление, V{\displaystyle V} — объём, ni{\displaystyle n_{i}} — количество (или масса) i{\displaystyle i}-го составляющего систему вещества, μi{\displaystyle \mu _{i}} — химический потенциал этого вещества (см. Энтропия открытой системы).

Для бесконечно малого^[13]квазистатического изохорного процесса (V=const{\displaystyle V=const})

dU=TdS+∑i=1kμidni;{\displaystyle dU=TdS+\sum _{i=1}^{k}\mu _{i}dn_{i};}

(Изменение внутренней энергии в бесконечно малом квазистатическом изохорном процессе)

для бесконечно малого квазистатического изобарного процесса (P=const{\displaystyle P=const})

dH=TdS+∑i=1kμidni.{\displaystyle dH=TdS+\sum _{i=1}^{k}\mu _{i}dn_{i}.}

(Изменение энтальпии в бесконечно малом квазистатическом изобарном процессе)

Важно понимать, что представление о теплоте химической реакции при сохранении исторически сложившегося названия (восходящего ко временам, когда любое изменение температуры связывали с поглощением или выделением теплоты) уже не имеет прямого отношения к общефизическому понятию количества теплоты. Действительно, при химической реакции в изолированной системе (например, инициируемом электрической искрой взрыве гремучего газа в герметически закрытом термосе) может иметь место изменение температуры (за счёт изменения состава системы), но не происходит ни выделения/поглощения теплоты^[14], ни изменения внутренней энергии системы. Наконец, традиционная трактовка теплоты, основанная на представлении об адиабатической изоляции системы от окружающей среды^[15] (см. Неоднозначность понятий «теплота» и «работа») к открытым системам не применима, и для них теплоту q{\displaystyle q} бесконечно малого квазистатического процесса полагают равной^[16][17]

q≡TdS.{\displaystyle q\equiv TdS.}

(Дефиниция теплоты для любого бесконечно малого квазистатического процесса)

Таким образом, теплота бесконечно малого квазистатического изохорного процесса qV{\displaystyle q_{V}} равна

qV=dU−∑i=1kμidni,{\displaystyle q_{V}=dU-\sum _{i=1}^{k}\mu _{i}dn_{i},}

(Теплота бесконечно малого квазистатического изохорного процесса)

а теплота бесконечно малого квазистатического изобарного процесса qP{\displaystyle q_{P}} равна

qP=dH−∑i=1kμidni.{\displaystyle q_{P}=dH-\sum _{i=1}^{k}\mu _{i}dn_{i}.}

(Теплота бесконечно малого квазистатического изобарного процесса)

Для закрытых систем изменение энергии системы за счёт изменения масс составляющих систему веществ (химическую работу^{[18][19][20][21][22]}, работу перераспределения масс составляющих систему веществ^[23]) ∑iμidni{\displaystyle \sum _{i}\mu _{i}dn_{i}} учитывать не требуется^[24][25], и выражения для теплот ещё более упрощаются:

qV=dU,{\displaystyle q_{V}=dU,}

(Теплота бесконечно малого квазистатического изохорного процесса в простой закрытой системе)

qP=dH.{\displaystyle q_{P}=dH.}

(Теплота бесконечно малого квазистатического изобарного процесса в простой закрытой системе)

Из сказанного ясно, почему в дефиниции теплового эффекта химической реакции фигурируют внутренняя энергия, энтальпия и запрет на любые виды работ в системе, кроме работы расширения/сжатия. Уточним, что в понятии «химическая работа» термин «работа» не имеет отношения к понятию «термодинамическая работа» и использован просто как синоним словосочетания «изменение энергии». Наконец, подчеркнём, что когда речь идёт о тепловом эффекте химической реакции, то, как и во многих других случаях, касающихся термохимии, подразумевается, что речь идёт о закрытой системе и полномасштабное применение мощного, но громоздкого математического аппарата термодинамики систем переменного состава не требуется^[24][25][26].

Энергетический эффект химической реакции всегда рассматривают применительно к конкретному термохимическому уравнению, которое может не иметь отношения к реальному химическому процессу. Термохимическое уравнение лишь показывает, какие наборы начальных и конечных индивидуальных веществ, находящихся в определенных состояниях и количественных соотношениях, исчезают и образуются. В начальном состоянии должны присутствовать только исходные вещества (реактанты), а в конечном — только продукты химической реакции. Единственным условием при записи термохимического уравнения является соблюдение материального и зарядового баланса. Вещества в растворённом или адсорбированном состоянии тоже считаются индивидуальными соединениями; если растворитель или адсорбент не участвует непосредственно в химической реакции и не реагирует с растворённым веществом, то он рассматривается просто как фактор, влияющий на термодинамические свойства рассматриваемого вещества. Наконец, в термохимическом уравнении могут фигурировать частицы, не способные к самостоятельному существованию (электроны, протоны, ионы, радикалы, атомарные простые вещества)^[27].

Энергетический эффект реального процесса с химической реакцией зависит от условий проведения процесса и не может служить стандартной характеристикой конкретной химической реакции^[3]. Химическая же термодинамика нуждается в показателе, связанном с энергетикой химической реакции, но не зависящем от условий её проведения. Покажем, как может быть получен интересующий нас показатель. Для этого рассмотрим следующий мысленный эксперимент. Возьмем чистые индивидуальные исходные вещества в мольных количествах, соответствующих стехиометрическим коэффициентам интересующего нас термохимического уравнения, и находящиеся при определенных температуре и давлении. Если привести эти вещества в контакт, то энтальпия образовавшейся неравновесной системы в начальный момент времени будет равна сумме энтальпий исходных веществ. Теперь рассмотрим конечное состояние изучаемой системы в предположении, что реактанты прореагировали полностью^[28] и продукты реакции находятся при той же температуре и том же давлении, что и реактанты. Энтальпия системы (в общем случае неравновесной) из продуктов химической реакции будет равна сумме энтальпий этих веществ. Поскольку энтальпия — функция состояния, то разность энтальпий ΔH{\displaystyle \Delta H} системы в конце и начале рассмотренного мысленного эксперимента не зависит от условий проведения химической реакции. Эту разность энтальпий и называют изобарным тепловым эффектом (термохимической теплотой) химической реакции, соответствующей определённому термохимическому уравнению^[29][30]. Важно, что реальная осуществимость рассмотренного мысленного эксперимента, гипотетические условия его проведения и неравновесность исходного и конечного состояний термохимической системы не сказываются на дефиниции теплового эффекта химической реакции.

Часто тепловой эффект химической реакции относят к 1 молю одного из продуктов реакции^[31].

Резюмируем сказанное: теплота процесса, связанного с фактическим протеканием химической реакции, и энергетический эффект химической реакции отнюдь не одно и то же, а дефиниция теплового эффекта химической реакции вообще не предполагает действительного осуществления реакции, соответствующей рассматриваемому термохимическому уравнению^[32].

И внутренняя энергия, и энтальпия представляют собой функции состояния, поэтому тепловой эффект химической реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, то есть от числа и характера промежуточных стадий (закон Гесса)^{[33][34][35][36]}.

Тепловой эффект химической реакции, протекающей при постоянном давлении, и равный изменению энтальпии системы в процессе, соответствующем термохимическому уравнению, называется изобарным тепловым эффектом или энтальпией химической реакции. Тепловой эффект химической реакции, протекающей при постоянном объёме, и равный изменению внутренней энергии системы в процессе, соответствующем термохимическому уравнению, называют изохорным тепловым эффектом^[2].

Для отдельных типов химических реакций вместо общего термина «тепловой эффект химической реакции» используют специальные (сокращённые) термины: теплота образования, теплота сгорания и т. п.^[1]

Дефиниции тепловых эффектов должны быть дополнены указанием на начальные точки отсчёта значений энергии и энтальпии. Для сравнения тепловых эффектов и упрощения термодинамических расчётов все величины тепловых эффектов реакций относят к стандартным условиям (все вещества находятся в стандартных состояниях)^[1]. Если реакцию — реально или гипотетически — проводят при стандартных условиях (T = 298,15 К = 25 °С и P = 1 бар = 100 кПа)^[37], то тепловой эффект называют стандартным тепловым эффектом реакции или стандартной энтальпией реакции ΔHo
r.

Химические реакции, сопровождающиеся повышением температуры, называют экзотермическими, понижением температуры — эндотермическими. В термодинамической системе знаков тепловой эффект экзотермической реакции (ΔU<0{\displaystyle \Delta U<0} или ΔH<0{\displaystyle \Delta H<0}) считают отрицательным, эндотермической (ΔU>0{\displaystyle \Delta U>0} или ΔH>0{\displaystyle \Delta H>0}) — положительным. В устаревшей и не рекомендуемой к употреблению термохимической системе знаков положительным, наоборот, считается тепловой эффект экзотермической реакции, а отрицательным — эндотермической^[38].

Тепловые эффекты химических реакций важны для теоретической химии и необходимы при расчётах равновесных составов смесей, выхода продуктов реакций, удельной тяги топлив реактивных двигателей и для решения многих других прикладных задач^[1].

Изучение тепловых эффектов химических реакций составляет важнейшую задачу термохимии^[3]. Для расчёта стандартных тепловых эффектов химических реакций используют таблицы стандартных теплот образования или сгорания^[38].

Стандартная энтальпия образования (стандартная теплота образования)[править | править код]

Под стандартной теплотой образования понимают тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.

Например, стандартная энтальпия образования 1 моля метана из углерода и водорода равна тепловому эффекту реакции:

С(тв) + 2H₂(г) = CH₄(г) + 74,9 кДж/моль.

Стандартная энтальпия образования обозначается ΔHo
f. Здесь индекс f означает formation (образование), а знак «O» в верхнем индексе указывает, что величина относится к стандартному состоянию вещества: один моль индивидуального химического соединения, взятого в чистом виде при стандартных условиях в том агрегатном состоянии, которое устойчиво в этих условиях (если нет специальной оговорки)^[39]. Иногда для обозначения стандартного состояния используют перечёркнутый символ «O» в верхнем индексе; согласно рекомендациям ИЮПАК по использованию обозначений в физической химии^[40], перечёркнутый и неперечёркнутый символ «O», используемые для обозначения стандартного состояния, одинаково приемлемы. В литературе часто встречается другое обозначение стандартной энтальпии — ΔHo
298,15, где знак «O» указывает на равенство давления одной атмосфере^[41] (или, несколько более точно, на стандартные условия^[42]), а 298,15 — температура. Иногда индекс «O» используют для величин, относящихся к чистому веществу, оговаривая, что обозначать им стандартные термодинамические величины можно только тогда, когда в качестве стандартного состояния выбрано именно чистое вещество^[43]. Стандартным также может быть принято, например, состояние вещества в предельно разбавленном растворе.

Энтальпия образования простых веществ принимается равной нулю, причем нулевое значение энтальпии образования относится к агрегатному состоянию, устойчивому при T = 298,15 K. Например, для иода в кристаллическом состоянии ΔH^o(I₂, тв) = 0 кДж/моль, а для жидкого иода ΔH^o(I₂, ж) = 22 кДж/моль. Энтальпии образования простых веществ при стандартных условиях являются их основными энергетическими характеристиками.

Тепловой эффект любой реакции находится как разность между суммой теплот образования всех продуктов и суммой теплот образования всех реагентов в данной реакции (следствие закона Гесса):

ΔH^o_{реакции} = ΣΔHo
f (продукты) — ΣΔHo
f (реагенты).

Термохимические эффекты можно включать в химические реакции. Химические уравнения в которых указано количество выделившейся или поглощенной теплоты, называются термохимическими уравнениями. Реакции, сопровождающиеся выделением тепла в окружающую среду имеют отрицательный тепловой эффект и называются экзотермическими. Реакции, сопровождающиеся поглощением тепла имеют положительный тепловой эффект и называются эндотермическими. Тепловой эффект обычно относится к одному молю прореагировавшего исходного вещества, стехиометрический коэффициент которого максимален.

Температурная зависимость теплового эффекта (энтальпии) реакции[править | править код]

Чтобы рассчитать температурную зависимость энтальпии реакции, необходимо знать мольные теплоемкости веществ, участвующих в реакции. Изменение энтальпии реакции при увеличении температуры от Т₁ до Т₂ рассчитывают по закону Кирхгофа (предполагается, что в данном интервале температур мольные теплоемкости не зависят от температуры и нет фазовых превращений):

ΔH(T2)=ΔH(T1)+∫12ΔCp(T1,T2)d(T).{\displaystyle \Delta {H(T_{2})}=\Delta {H(T_{1})}+\int \limits _{1}^{2}{\Delta {C_{p}}(T_{1}{,}T_{2})d(T)}.}

Если в данном интервале температур происходят фазовые превращения, то при расчёте необходимо учесть теплоты соответствующих превращений, а также изменение температурной зависимости теплоемкости веществ, претерпевших такие превращения:

ΔH(T2)=ΔH(T1)+∫1TφΔCp(T1,Tφ)d(T)+∫Tφ2ΔCp(Tφ,T2)d(T),{\displaystyle \Delta {H(T_{2})}=\Delta {H(T_{1})}+\int \limits _{1}^{T_{\varphi }}{\Delta {C_{p}}(T_{1}{,}T_{\varphi })d(T)}+\int \limits _{T_{\varphi }}^{2}{\Delta {C_{p}}(T_{\varphi }{,}T_{2})d(T)},}

где ΔC_p(T₁, T_φ) — изменение теплоемкости в интервале температур от Т₁ до температуры фазового перехода; ΔC_p(T_φ, T₂) — изменение теплоемкости в интервале температур от температуры фазового перехода до конечной температуры, и T_φ — температура фазового перехода.

Стандартная энтальпия сгорания — ΔHо
гор., тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Теплота сгорания негорючих веществ принимается равной нулю.

Стандартная энтальпия растворения — ΔHо
раств., тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Складывается из теплоты разрушения кристаллической решётки и теплоты гидратации (или теплоты сольватации для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием соединений переменного состава — гидратов (сольватов). Разрушение кристаллической решетки, как правило, эндотермический процесс — ΔH_реш. > 0, а гидратация ионов — экзотермический, ΔH_гидр. < 0. В зависимости от соотношения значений ΔH_реш. и ΔH_гидр. энтальпия растворения может иметь как положительное, так и отрицательное значение. Так растворение кристаллического гидроксида калия сопровождается выделением тепла:

ΔHо
раств.KOH = ΔHо
реш. + ΔHо
гидр.К⁺ + ΔHо
гидр.OH⁻ = −59 кДж/моль.

Под энтальпией гидратации ΔH_гидр. понимается теплота, которая выделяется при переходе 1 моля ионов из вакуума в раствор.

Стандартная энтальпия нейтрализации[править | править код]

Стандартная энтальпия нейтрализации ΔHо
нейтр. — энтальпия реакции взаимодействия сильных кислот и оснований с образованием 1 моля воды при стандартных условиях:

HCl + NaOH = NaCl + H₂O

H⁺ + OH⁻ = H₂O, ΔHо
нейтр. = −55,9 кДж/моль

Стандартная энтальпия нейтрализации для концентрированных растворов сильных электролитов зависит от концентрации ионов, вследствие изменения значения ΔHо
гидратации ионов при разбавлении.

1. ↑ В общем случае, когда не выполняются условия, перечисленные в дефиниции теплового эффекта химической реакции, говорят об энергетическом эффекте химической реакции^[4][5][6][7], который при выполнении упомянутых выше условий сводится к выделению/поглощению системой теплоты, то есть именно к тепловому эффекту. В соответствии со сложившейся в термохимии традицией термины «энергетический эффект химической реакции» и «тепловой эффект химической реакции» до сих пор иногда рассматривают как синонимы^[8][9].

1. ↑ ^{1 2 3 4} БСЭ, 3-е изд., т. 25, 1976, с. 450.
2. ↑ ^{1 2} Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 16.
3. ↑ ^{1 2 3} Химическая энциклопедия, т. 4, 1995, с. 522—523.
4. ↑ Александров Н. Е. и др., Основы теории тепловых процессов и машин, ч. 2, 2015, с. 290.
5. ↑ Морачевский А. Г., Фирсова Е. Г., Физическая химия. Термодинамика химических реакций, 2015, с. 21.
6. ↑ Карякин Н. В., Основы химической термодинамики, 2003, с. 17, 63.
7. ↑ Шмидт Э., Введение в техническую термодинамику, 1965, с. 311.
8. ↑ Александров Н. Е. и др., Основы теории тепловых процессов и машин, ч. 2, 2015, с. 174.
9. ↑ Нараев В. Н., Физическая химия, ч. 1, 2007, с. 6.
10. ↑ Состояние простой термодинамической системы (газы и изотропные жидкости в ситуации, когда поверхностными эффектами и наличием внешних силовых полей можно пренебречь) полностью задано её объёмом, давлением в системе и массами составляющих систему веществ.
11. ↑ Кубо Р., Термодинамика, 1970, с. 143.
12. ↑ Мюнстер А., Химическая термодинамика, 1971, с. 103.
13. ↑ Бесконечно малым (элементарным, инфинитезимальным) называют процесс, для которого разница между начальным и конечным состояниями системы бесконечно мала.
14. ↑ Под теплотой здесь подразумевается изменение энергии системы в результате теплопередачи через граничную поверхность (см. Теплота).
15. ↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 8.
16. ↑ Базаров И. П., Термодинамика, 2010, с. 114.
17. ↑ Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 54.
18. ↑ Lebon G. e. a., Understanding Non-equilibrium Thermodynamics, 2008, p. 14.
19. ↑ Жариков В. А., Основы физической геохимии, 2005, с. 31.
20. ↑ Callen H. B., Thermodynamics and an Introduction to Thermostatistics, 1985, p. 36.
21. ↑ Сычёв В. В., Сложные термодинамические системы, 2009, с. 257.
22. ↑ Путилов К. А., Термодинамика, 1971, с. 125.
23. ↑ Тамм М. Е., Третьяков Ю. Д., Физико-химические основы неорганической химии, 2004, с. 11.
24. ↑ ^{1 2} Степановских Е. И. и др., Химическая термодинамика в вопросах и ответах, 2014, с. 87.
25. ↑ ^{1 2} Бурдаков В. П. и др., Термодинамика, ч. 2, 2009, с. 10.
26. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 127.
27. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 128.
28. ↑ То, что конечное состояние может оказаться недостижимым в действительности, применительно к данному рассмотрению не имеет значения.
29. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 130.
30. ↑ Морачевский А. Г., Кохацкая М. С., Прикладная химическая термодинамика, 2008, с. 24.
31. ↑ Никольский Б. П. и др., Физическая химия, 1987, с. 17.
32. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 131.
33. ↑ Ляшков В. И., Теоретические основы теплотехники, 2015, с. 102.
34. ↑ Морачевский А. Г., Кохацкая М. С., Прикладная химическая термодинамика, 2008, с. 23.
35. ↑ Кнорре Д.Г. и др., Физическая химия, 1990, с. 245.
36. ↑ Никольский Б. П. и др., Физическая химия, 1987, с. 18.
37. ↑ До 1982 года ИЮПАК принимал в качестве стандартного давления 1 атм = 101325 Па; это следует учитывать при использовании данных из литературы, изданной ранее.
38. ↑ ^{1 2} Химический энциклопедический словарь, 1983, с. 563.
39. ↑ Курс физической химии // Под ред. Я. И. Герасимова. М.-Л.: Химия, 1964. — Т. 1. — С. 55.
40. ↑ International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. p. 49. Electronic version.
41. ↑ Жуховицкий А. А., Шварцман Л. А. Физическая химия. — М.: Металлургия, 1976. — 544 с.
42. ↑ Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов / Под ред. А. Г. Стромберга. — 2-е изд. — М.: Высш. шк., 1988. — 496 с.
43. ↑ Пригожин И., Дефэй Р. Химическая термодинамика = Chemical Thermodynamics / Перевод с англ. под ред. В. А. Михайлова. — Новосибирск: Наука, 1966. — 502 с.

• Callen H. B. Thermodynamics and an Introduction to Thermostatistics. — 2nd ed. — N. Y. e. a.: John Wiley, 1985. — XVI + 493 p. — ISBN 0471862568, 9780471862567.
• Lebon G., Jou D., Casas-Vázquez J. Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers. — Berlin — Heidelberg: Springer, 2008. — XIII + 325 p. — ISBN 978-3-540-74251-7, 978-3-540-74252-4. — doi:10.1007/978-3-540-74252-4.
• Александров Н. Е., Богданов А. И., Костин К. И. и др. Основы теории тепловых процессов и машин. Часть II / Под ред. Н. И. Прокопенко. — 5-е изд. (электронное). — М.: Бином. Лаборатория знаний, 2015. — 572 с. — ISBN 978-5-9963-2613-6. (недоступная ссылка)
• Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
• Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: Советская Энциклопедия, 1976. — Т. 25: Струнино — Тихорецк. — 600 с. Архивная копия от 5 августа 2017 на Wayback Machine
• Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М: Инфра-М, 2017. — 868 с. — ISBN 978-5-16-104227-4.
• Бурдаков В. П., Дзюбенко Б. В., Меснянкин С. Ю., Михайлова Т. В. Термодинамика. Часть 2. Специальный курс. — М.: Дрофа, 2009. — 362 с. — (Высшее образование. Современный учебник). — ISBN 978-5-358-06140-8.
• Жариков В. А. Основы физической геохимии. — М.: Наука; Изд-во МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
• Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
• Карякин Н. В. Основы химической термодинамики. — М.: Академия, 2003. — 463 с. — (Высшее профессиональное образование). — ISBN 5-7695-1596-1. (недоступная ссылка)
• Кнорре Д. Г., Крылова Л. Ф., Музыкантов В. С. Физическая химия. — 2. — М.: Высшая школа, 1990. — 416 с. — ISBN 5-06-000655-7.
• Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
• Ляшков В. И. Теоретические основы теплотехники. — М.: Курс; Инфра-М, 2015. — 328 с. — ISBN 978-5-905554-85-8, 978-5-16-0І0639-7.
• Морачевский А. Г., Кохацкая М. С. Прикладная химическая термодинамика. — СПб.: Изд-во Политехн. ун-та, 2008. — 254 с. — ISBN 978-5-7422-2006-0.
• Морачевский А. Г., Фирсова Е. Г. Физическая химия. Термодинамика химических реакций. — 2-е изд., испр. — СПб.: Лань, 2015. — 101 с. — (Учебники

для вузов. Специальная литература). — ISBN 978-5-8114-1858-9. (недоступная ссылка)

• Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — М.: Мир, 1971. — 296 с.
• Нараев В. Н. Физическая химия. Часть 1. Химическая термодинамика. Фазовые равновесия и учение о растворах. Электрохимия. — СПб.: Санкт-Петербургский государственный технологический институт (Технический университет), 2007. — 262 с. (недоступная ссылка)
• Никольский Б. П., Смирнова Н. А., Панов М. Ю. и др. Физическая химия. Теоретическое и практическое руководство / Под ред. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с. — (Для высшей школы).
• Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
• Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: УИПЦ, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
• Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
• Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
• Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
• Химическая энциклопедия / Гл. ред. Н. С. Зефиров. — М.: Большая Российская энциклопедия, 1995. — Т. 4: Пол — Три. — 640 с. —

Удельная теплота плавления — Википедия

Материал из Википедии — свободной энциклопедии

Уде́льная теплота́ плавле́ния (также: энтальпия плавления; также существует равнозначное понятие уде́льная теплота́ кристаллиза́ции) — количество теплоты, которое необходимо сообщить одной единице массы кристаллического вещества в равновесном изобарно-изотермическом процессе, чтобы перевести его из твёрдого (кристаллического) состояния в жидкое (то же количество теплоты выделяется при кристаллизации вещества).

Единица измерения — Дж/кг. Теплота плавления — частный случай теплоты термодинамического фазового перехода.

Удельная теплота плавления обозначается буквой λ{\displaystyle \lambda } (греческая буква лямбда). Формула расчёта удельной теплоты плавления:

λ=Qm,{\displaystyle \lambda ={\frac {Q}{m}},}

где Q{\displaystyle Q} — количество теплоты, полученное веществом при плавлении (или выделившееся при кристаллизации), m{\displaystyle m} — масса плавящегося (кристаллизующегося) вещества. Удельная теплота плавления всегда положительна; единственное известное исключение — гелий под высоким давлением^[1][2].

Значения удельной теплоты плавления некоторых веществ[править | править код]

• Енохович А. С. Краткий справочник по физике. — М.: «Высшая школа», 1976. — С. 114. — 288 с.

1. ↑ Atkins, Peter & Jones, Loretta (2008), Chemical Principles: The Quest for Insight (4th ed.), W. H. Freeman and Company, с. 236, ISBN 0-7167-7355-4 
2. ↑ Hoffer J. K., Gardner W. R., Waterfield C. G., Phillips N. E. Thermodynamic properties of ⁴He. II. The bcc phase and the P-T and VT phase diagrams below 2 K (англ.) // Journal of Low Temperature Physics (англ.)русск. : journal. — 1976. — April (vol. 23, no. 1). — P. 63—102. — doi:10.1007/BF00117245. — Bibcode: 1976JLTP…23…63H.

Приведённое количество теплоты — Википедия

Приведённое количество теплоты — элементарное количество теплоты δQ{\displaystyle \delta Q}, полученное термодинамической системой в бесконечно малом процессе, при абсолютной температуре T{\displaystyle T}^[1]. Определяется отношением δQ/T{\displaystyle \delta Q/T}. Понятие в термодинамику было введено Клаузиусом.

Содержание

• 1 Неравенство Клаузиуса
• 2 Энтропия
• 3 См. также
• 4 Примечания

Основная статья: Неравенство Клаузиуса

Приведённое количество теплоты, полученное системой при любом круговом процессе, неположительно:

∮⁡δQT≤0{\displaystyle \oint {\frac {\delta Q}{T}}\leq 0}.

(1)

Основная статья: Энтропия

Разность энтропий в двух равновесных состояниях 1 и 2, по определению, равна приведённому количеству тепла, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути^[1]:

ΔS1→2=S2−S1=∫1→2δQT{\displaystyle \Delta S_{1\to 2}=S_{2}-S_{1}=\int \limits _{1\to 2}{\frac {\delta Q}{T}}}.

(2)

• Неравенство Клаузиуса
• Энтропия
• Теплота

1. ↑ ^{1 2} Сивухин Д. В. Общий курс физики. — М., 1979. — Т. II. Термодинамика и молекулярная физика. — С. 127.

Это заготовка статьи по физике. Вы можете помочь проекту, дополнив её.

Удельная теплоёмкость — урок. Физика, 8 класс.

Для того чтобы нагреть на определённую величину тела, взятые при одинаковой температуре, изготовленные из различных веществ, но имеющие одинаковую массу, требуется разное количество теплоты.

Пример:

Для нагревания \(1\) кг воды на \(1 \)°С требуется количество теплоты, равное \(4200\) Дж. А если нагревать \(1\) кг цинка на \(1\) °С, то потребуется всего \(400\) Дж. 

Физическая величина, численно равная количеству теплоты, которое необходимо передать веществу массой \(1\) кг для того, чтобы его температура изменилась на \(1\) °С, называется удельной теплоёмкостью вещества.

Обрати внимание!

Удельная теплоёмкость обозначается буквой \(с\) и измеряется в Дж/(кг·°С).

Пример:

Удельная теплоёмкость серебра равна \(250\) Дж/(кг·°С). Это означает, что для нагревания серебра массой \(1\) кг на \(1\) °С необходимо количество теплоты, равное \(250\) Дж.

При охлаждении серебра массой \(1\) кг на \(1\) °С выделится количество теплоты, равное \(250\) Дж.

Это означает, что если меняется температура серебра массой \(1\) кг на \(1\) °С, то оно или поглощает, или выделяет количество теплоты, равное \(250\) Дж.

Таблица 1. Удельная теплоёмкость некоторых веществ.

 

Твёрдые вещества

Вещество	\(c\), Дж/(кг·°С)
Алюминий	\(920\)
Бетон	\(880\)
Дерево	\(2700\)
Железо, сталь	\(460\)
Золото	\(130\)
Кирпич	\(750\)
Латунь	\(380\)
Лёд	\(2100\)
Медь	\(380\)
Нафталин	\(1300\)
Олово	\(250\)
Парафин	\(3200\)
Песок	\(970\)
Платина	\(130\)
Свинец	\(120\)
Серебро	\(250\)
Стекло	\(840\)
Цемент	\(800\)
Цинк	\(400\)
Чугун	\(550\)
Сера	\(710\)

 

Жидкости

Вещество	\(c\), Дж/(кг·°C)
Вода	\(4200\)
Глицерин	\(2400\)
Железо	\(830\)
Керосин	\(2140\)
Масло подсолнечное	\(1700\)
Масло трансформаторное	\(2000\)
Ртуть	\(120\)
Спирт этиловый	\(2400\)
Эфир серный	\(2300\)

 

Газы (при постоянном давлении и температуре \(20\) °С)

Вещество	\(c\), Дж/(кг·°C)
Азот	\(1000\)
Аммиак	\(2100\)
Водород	\(14300\)
Водяной пар	\(2200\)
Воздух	\(1000\)
Гелий	\(5200\)
Кислород	\(920\)
Углекислый газ	\(830\)

 

Удельная теплоемкость реальных газов, в отличие от идеальных газов, зависит от давления и температуры. И если зависимостью удельной теплоемкости реальных газов от давления в практических задачах можно пренебречь, то зависимость удельной теплоемкости газов от температуры необходимо учитывать, поскольку она очень существенна.

 

Обрати внимание!

Удельная теплоёмкость вещества, находящегося в различных агрегатных состояниях, различна.

Пример:

Вода в жидком состоянии имеет удельную теплоёмкость, равную \(4200\) Дж/(кг·°С), в твёрдом состоянии (лёд) — \(2100\) Дж/(кг·°С), в газообразном состоянии (водяной пар) — \(2200\) Дж/(кг·°С).

Вода — вещество особенное, обладающее самой высокой среди жидкостей удельной теплоёмкостью. Но самое интересное, что теплоёмкость воды снижается при температуре от \(0\) °С до \(37\) °С и снова растёт при дальнейшем нагревании.

 

 

В связи с этим вода в морях и океанах, нагреваясь летом, поглощает из окружающей среды огромное количество теплоты. А зимой вода остывает и отдаёт в окружающую среду большое количество теплоты. Поэтому в районах, расположенных вблизи водоёмов, летом не бывает очень жарко, а зимой очень холодно.

 

 

Из-за высокой удельной теплоёмкости воду широко используют в технике и быту. Например, в отопительных системах домов, при охлаждении деталей во время их обработки на станках, в медицине (в грелках) и др.

 

 

Именно благодаря высокой удельной теплоёмкости вода является одним из лучших средств для борьбы с огнём. Соприкасаясь с пламенем, она моментально превращается в пар, отнимая большое количество теплоты у горящего предмета.

 

 

Помимо непосредственного отвода тепла, вода гасит пламя ещё и косвенным образом. Водяной пар, образующийся при контакте с огнём, окутывает горящее тело, предотвращая поступление кислорода, без которого горение невозможно.

Какой водой эффективнее тушить огонь: горячей или холодной? Горячая вода тушит огонь быстрее, чем холодная. Дело в том, что нагретая вода скорее превратится в пар, а значит, и отсечёт поступление воздуха к горящему объекту.

 

Источники:

Пёрышкин А.В. Физика, 8 кл.: учебник. — М.: Дрофа, 2013. — 237 с.

www.infourok.ru

www.puzzleit.ru

www.libma.ru

www.englishhelponline.files.wordpress.com

www.avd16.ru

Удельная теплота парообразования и конденсации — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 декабря 2018; проверки требуют 6 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 декабря 2018; проверки требуют 6 правок.

Уде́льная теплота́ парообразова́ния и конденса́ции — физическая величина, показывающая, какое количество теплоты необходимо, чтобы обратить количество жидкости с единичной массой в пар , при данной температуре жидкости и без её изменения (температуры) в процессе испарения. Равна удельной теплоте конденсации единичной массы пара в жидкость.

Удельная теплота парообразования и конденсации обозначается буквой L{\displaystyle L}. Рассчитывается по формуле:

L=Qm,{\displaystyle L={\,Q \over m},}

где Q — теплота, истраченная на превращение жидкости в пар или пара в жидкость, m — масса.

Наименьшее значение удельной теплоты парообразования будет при температуре кипения жидкости.

Размерность удельной теплоты парообразования в СИ — Дж/кг. Устаревшие, но иногда применяемые единицы для теплоты парообразования — ккал/кг и кал/кг.

В химии теплота парообразования обычно приводится к молю вещества. Эта величина называется молярной теплотой испарения (конденсации); единица её измерения — Дж/моль. Также используются устаревшие единицы: ккал/моль, кал/моль.

Удельная теплота парообразования некоторых веществ при нормальном атмосферном давлении (760 мм. рт. ст. = 101,325 кПа) и температуре, равной температуре кипения вещества^[1]: