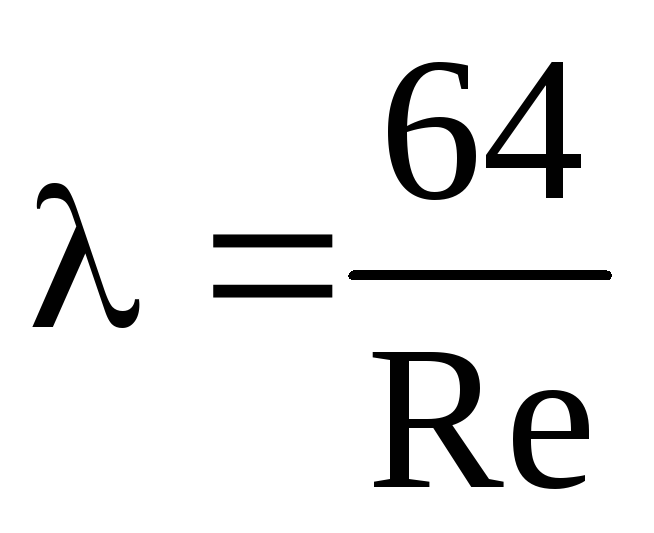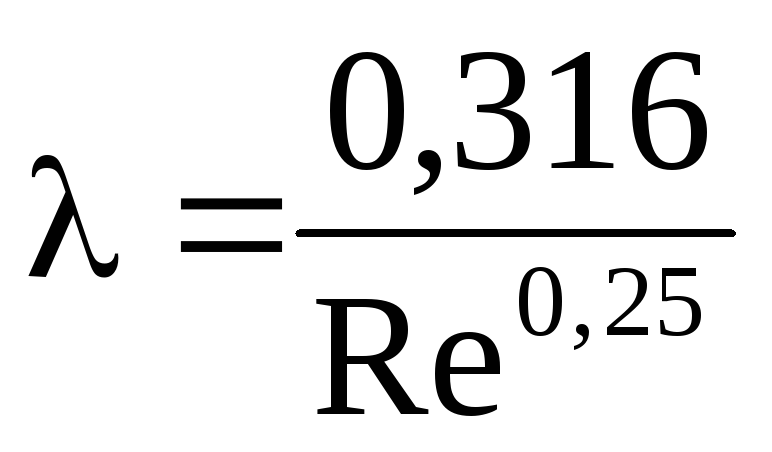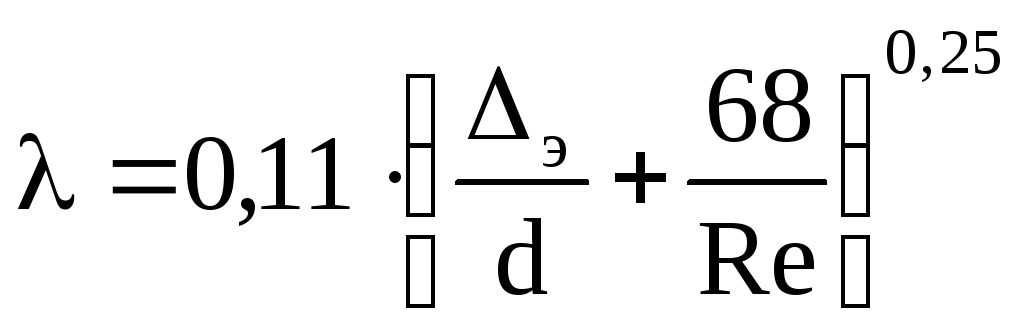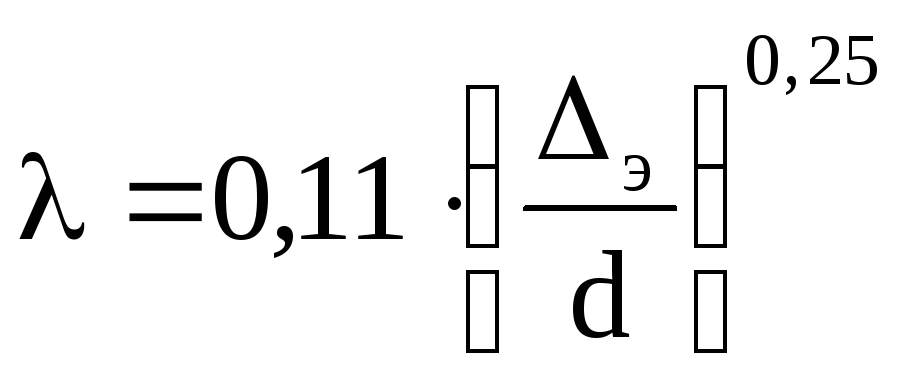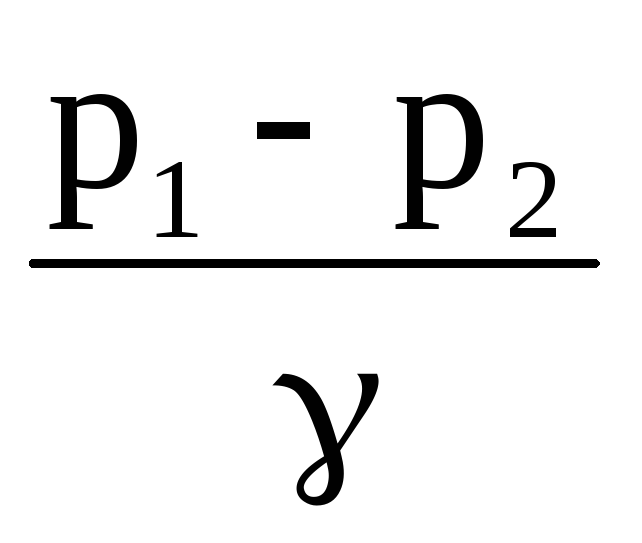Определение коэффициента гидравлического трения прямой трубы
Министерство образования и науки Российской Федерации
Национальный исследовательский ядерный университет «МИФИ»
Балаковский инженерно-технологический
Методические указания к выполнению лабораторной работы
по дисциплинам: «Гидравлика», «Механика жидкости и газа», «Водоснабжение и водоотведение с основами гидравлики», «Гидрогазодинамика», «Гидравлика и гидропневмопривод»
для студентов направлений: «Теплоэнергетика и теплотехника», «Строительство», «Конструкторско-технологическое обеспечение машиностроительных производств», «Строительство уникальных зданий и сооружений» », «Наземные транспортно-технологические средства»
профиль «Подъемно-транспортные, строительные, дорожные средства и оборудование»
очной, заочной и заочно-сокращенной форм обучения
Балаково 2015
Ц е л ь р а б о т ы:
1.Определить опытным путем коэффициент гидравлического трения.
2.Определить коэффициент гидравлического трения по теоретическим формулам и сравнить с опытным значением.
ОСНОВНЫЕ ПОНЯТИЯ
Потеря напора на трение по длине круглых труб hl oпределятся по формуле Дарси:
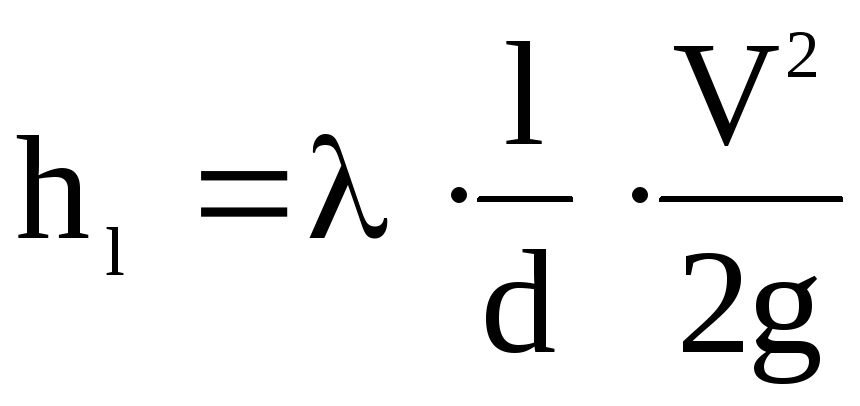 ,
(1)
,
(1)
где — коэффициент гидравлического трения;
d — диаметр трубы ;
V — средняя скорости жидкости;
g — ускорение силы тяжести, равное 981 см/с2 .
Многочисленными
экспериментами установлено, что
коэффициент гидравлического трения
зависит в общем случае от числа Рейнольдса
Re и относительной шероховатости стенок
трубы 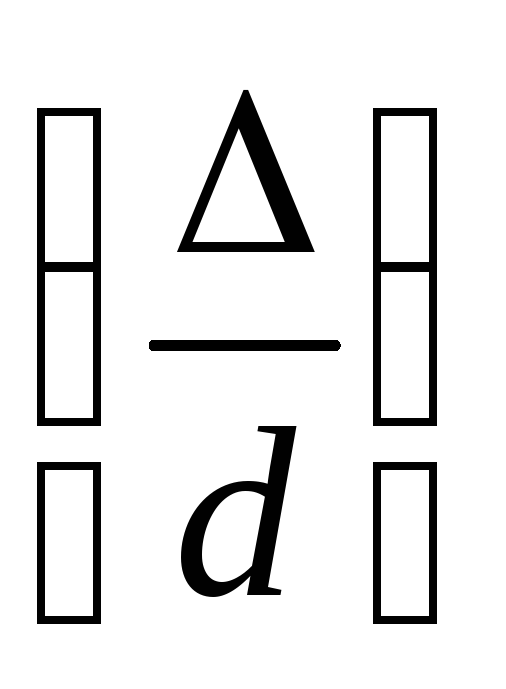 :
:
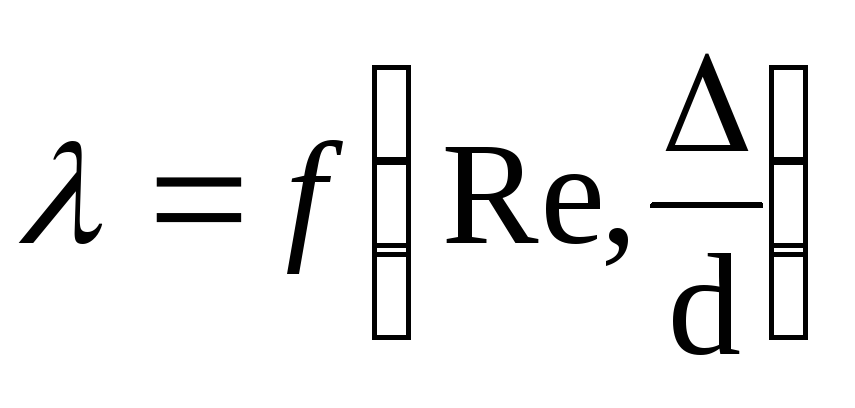
где — высота выступов шероховатости внутренних стенок трубы.
Преобладание того или иного фактора зависит от режима течения жидкости.
Существует пять зон гидравлического сопротивления.
1. З о н а в я з к о г о с о п р о т и в л е н и я.
Движение ламинарное, Re < 2300. В этой зоне шероховатость стенок мало влияет на потери напора
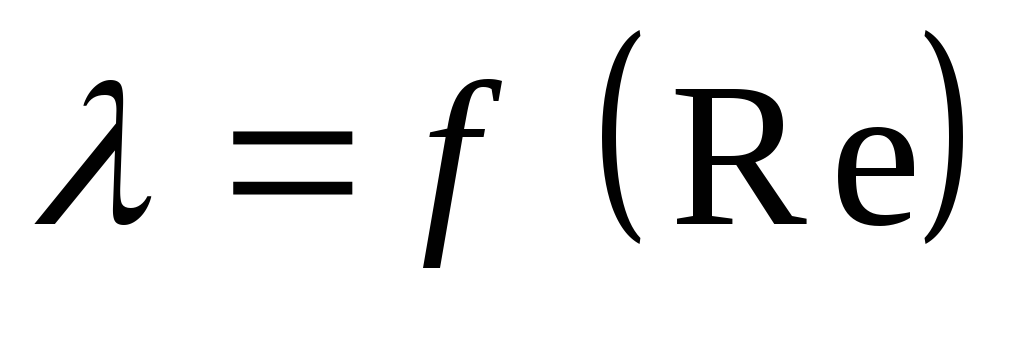 .
(3)
.
(3)
Теоретическая формула для определения коэффициента гидравлического трения для круглой трубы вытекает из закона Пуазейля :
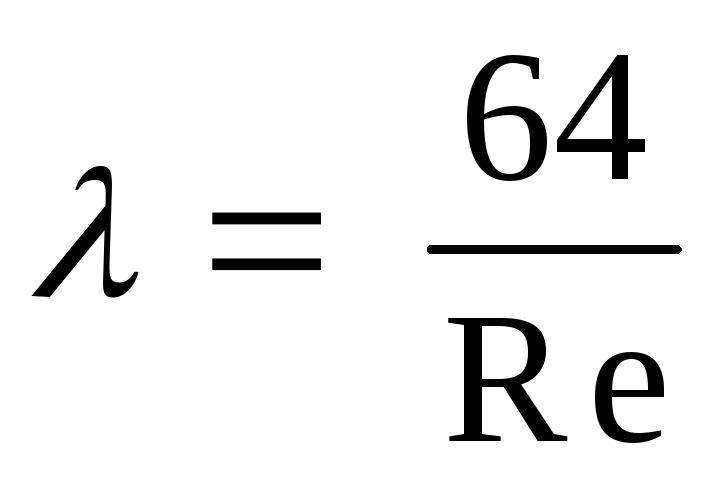 .
(4)
.
(4)
2. П е р е х о д н а я з о н а. При 2300 < Re < 4000 имеет место переходная зона, в которой движение уже не ламинарное и еще не турбулентное, т. е. здесь режим неустойчивый. Инженерные расчеты в этой зоне выполняются очень редко.
3. З о н а г
и д р а в л и ч е с к и г л а д к
и х т р у б. Движение турбулентное
4000 < Re < 10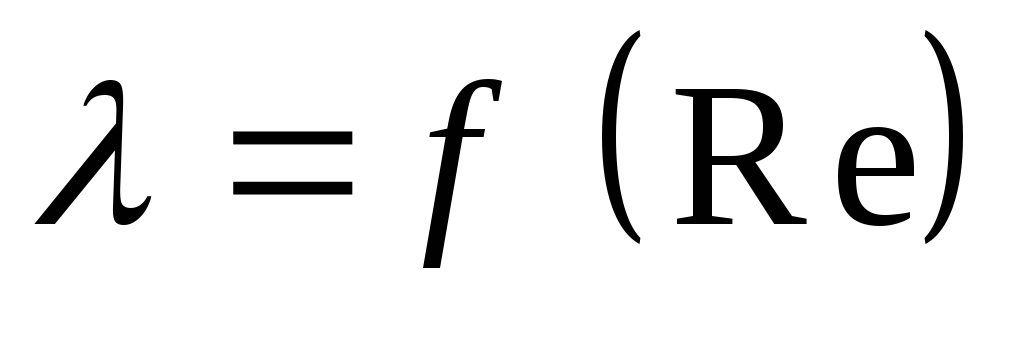 .
.
Для определения коэффициента гидравлического трения существует множество формул, однако, в данном методическом указании приводим лишь по одной, наиболее применимой. Для зоны гидравлически гладких труб можно воспользоваться формулой Блазиуса
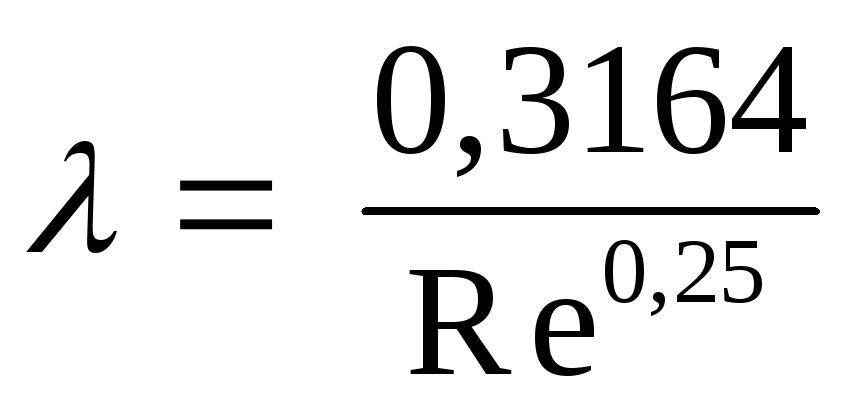 ;
(5)
;
(5)
4. З о н а д о к в а д р а т и ч н о г о с о п р о —
т и в л е н и я . Движение турбулентное. Ориентировочные границы зоны
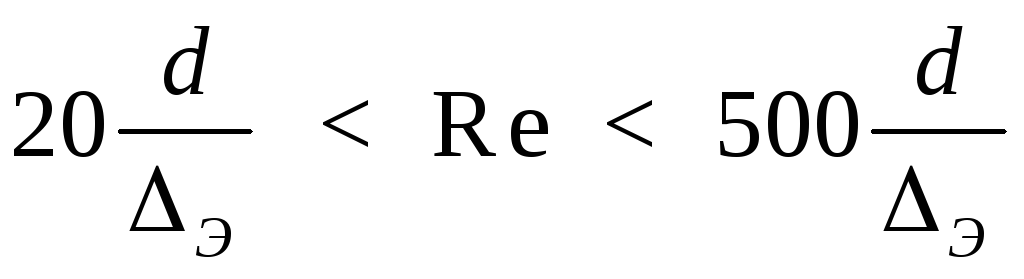 ,
,
где э- величина эквивалентной равномерно-зернистой шероховатости.
Под эквивалентной
шероховатостью понимают такую равномерно
— зернистую шероховатость, которая в
области квадратичного сопротивления
оказывает такое же сопротивление
движению жидкости как и труба с
естественной шероховатостью. В этой
зоне сопротивления коэффициент
гидравлического трения зависит от обеих
факторов 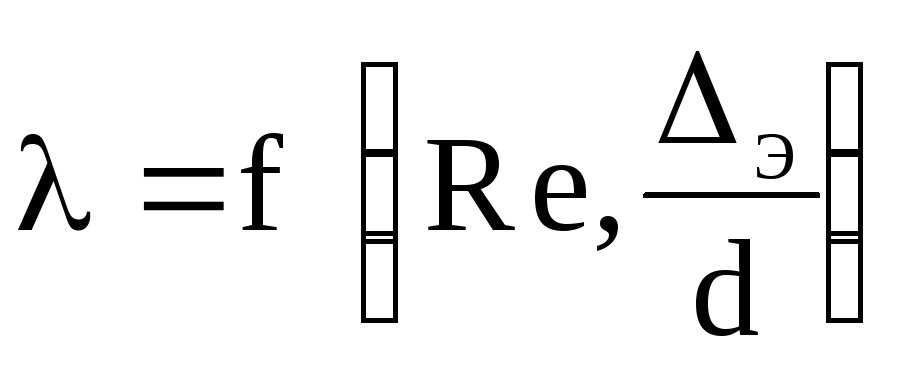
Для определения коэффициента гидравлического трения можно воспользоваться формулой А.Д. Альтшуля
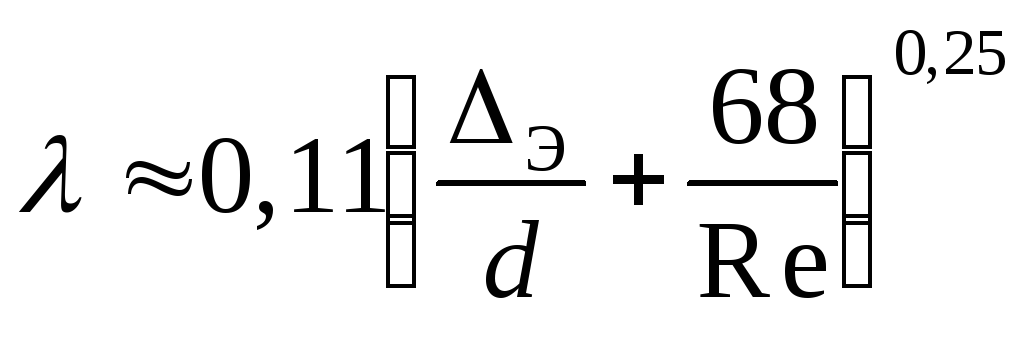 .
(6)
.
(6)
5. З о н а к в а д р а т и ч н о г о с о п р о т и в л е н и я.
Движение
турбулентное. Нижняя граница зоны 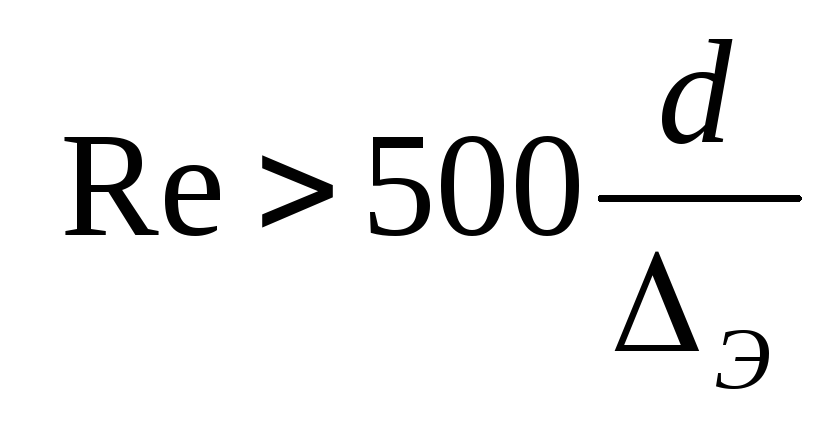 .
В этой зоне основным фактором, влияющим
на сопротивление, является шероховатость
стенок трубы
.
В этой зоне основным фактором, влияющим
на сопротивление, является шероховатость
стенок трубы 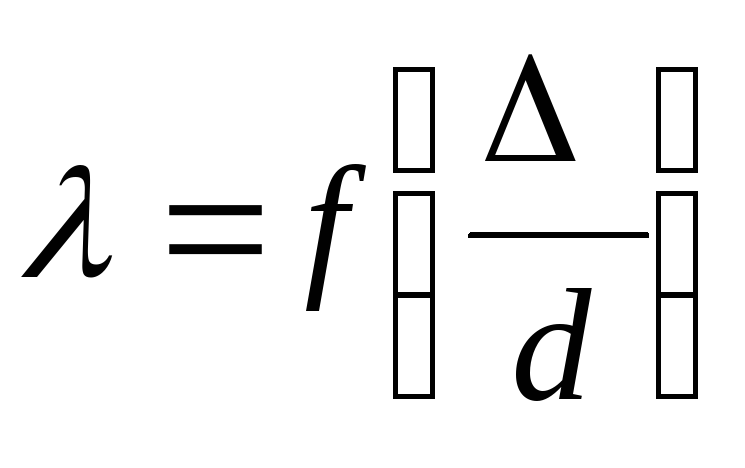 .
.
Для определения коэффициента гидравлического трения можно воспользоваться следующими формулой Б.Л.Шифринсона
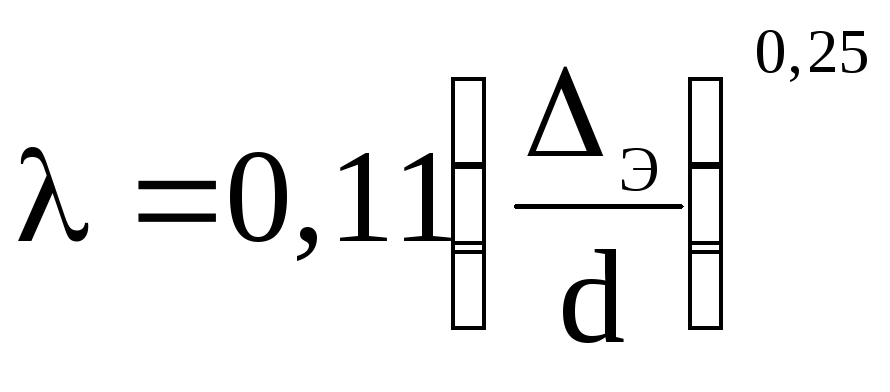 .
(7)
.
(7)
МЕТОДИКА ЭКСПЕРИМЕНТА
О п и с а н и е л а б о р а т о р н о й у с т а н о в к и
М е т о д и к а п р о в е д е н и я о п ы т о в
Перед проведением опытов напорный бак 1 заполняется водой. При этом вентиль 5 должен быть закрытым. Затем вентиль 5 открывается и задается расход Q в интервале 0 < Q <= Qmax. Обычно начинают с максимального расхода, соответствующего полному открытию вентиля 5. При проведении опытов необходимо поддерживать установившееся движение воды. Для этого при помощи вентиля 7 уровень воды в напорном баке 1
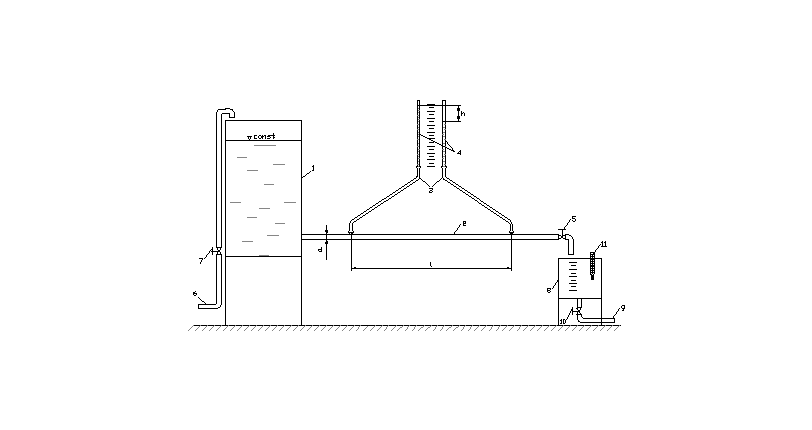 Схема лабораторной
установки
Схема лабораторной
установки
поддерживается постоянным. При заданном расходе воды выполняются следующие измерения. При помощи пьезометров 4 по шкале определяется разность уровней воды в них с погрешностью 0.5 мм. Линия визирования при этом должна быть перпендикулярна плоскости шкалы. Одновременно с этим определяется расход воды объемным способом при помощи мерной емкости 8 и секундомера
Температура жидкости необходима для определения кинематического коэффициента вязкости и измеряется в нижнем баке при помощи термометра с погрешностью ± 0,5 °С.
Расходы воды задаются с таким расчетом, чтобы в опытах охватить все зоны сопротивления.
ТРЕБОВАНИЯ БЕЗОПАСНОСТИ ТРУДА
1. Перед проведением опытов необходимо изучить инструкцию по правилам безопасности работы в лаборатории.
3. При проведении опыта аккуратно обращаться со стеклянными и хрупкими приборами и оборудованием лабораторной установки.
4. При возникновении затруднений в выполнении опытов, а также поломки приборов и оборудования, необходимо прекратить опыты и обратиться к преподавателю.
5. После завершения опытов доложить преподавателю и сдать приборы.
6. В случае получения травмы необходимо немедленно прекратить опыты и обратиться к преподавателю за медицинской помощью.
ПОРЯДОК ПРОВЕДЕНИЯ ОПЫТОВ
1. Подготовка установки к проведению опыта.
1.1. Открыть вентиль 7 и заполнить напорный бак 1 водой до уровня перелива напорного бака. При этом вентиль 5 должен быть закрытым.
1.3. Проверяется отсутствие течей воды в местах соединения гибких шлангов 3 и через вентили.
1.4. Определяются длина исследуемой трубы, внутренний диаметр, шероховатость стенок.
1.5. Определяют размеры мерной емкости.
2. Определение коэффициентов гидравлического трения опытным путем.
Максимальным открытием вентиля 5 устанавливают максимальный расход воды в трубе.
При помощи вентиля 7 добиваются постоянства уровня воды в напорном баке 1.
2.3. После достижения установившегося режима движения по шкале определяют разность уровней воды в пьезометрах 4. Результат записывают в таблицу.
2.4. Одновременно определяют расход воды объемным способом и измеряют температуру воды. При измерении расхода определяют время наполнения заданного объема мерной емкости.
2.6. После завершения всех измерений в данном опыте закрывается сначала вентиль 7, затем вентиль 5.
2.7. В таблице выполняются необходимые расчеты для установления зоны сопротивления .
2.8. Открывают вентиль 5 менее максимального, затем при помощи вентиля 7 добиваются постоянства уровня воды в напорном баке. Выполняют измерения аналогично первому опыту.
2.9. При проведении опытов добиваются, чтобы охватить все зоны сопротивления. Количество опытов должно быть не менее четырех.
2.10. После завершения всех опытов вентили 7 и 5 закрываются, вентиль 10 открывается и проверяется на отсутствие течей в вентилях, в местах соединения шлангов и в самих шлангах.
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
Результаты измерений и необходимых вычислений заносятся в таблицу.
1. Вычисляется площадь поперечного сечения трубы S:
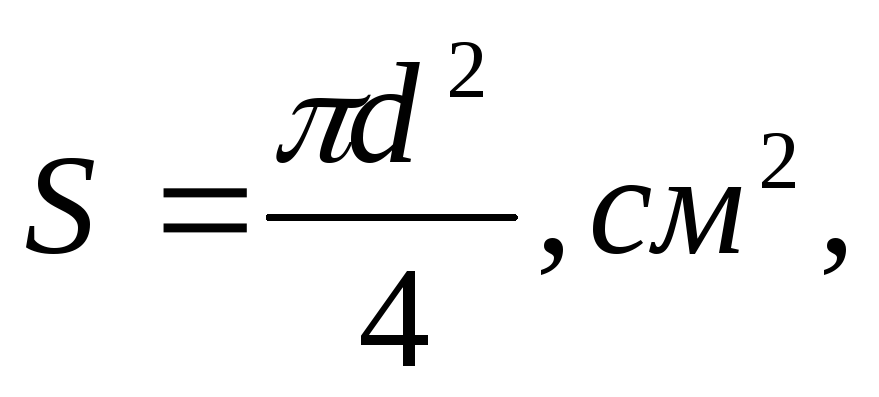 (8)
(8)
где d — внутренний диаметр трубы, см.
2. Вычисляется расход жидкости Q , см3/с.
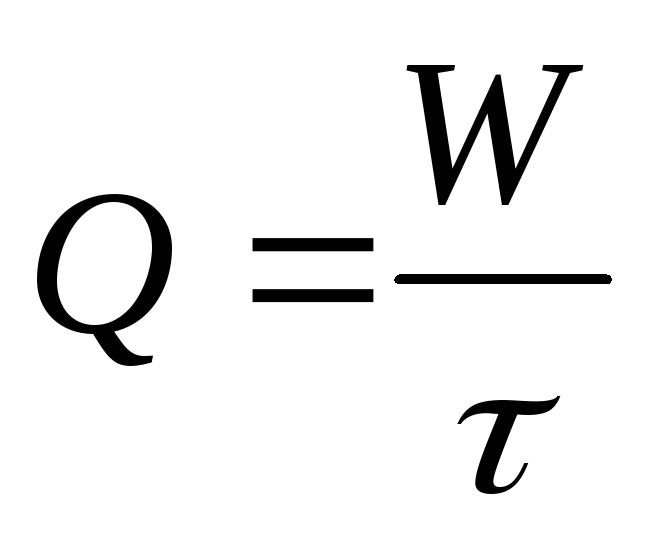 ,
(9)
,
(9)
где W — объем мерного сосуда, см3 ;
t — время наполнения мерного бака, с.
3. Вычисляется средняя скорость потока жидкости V:
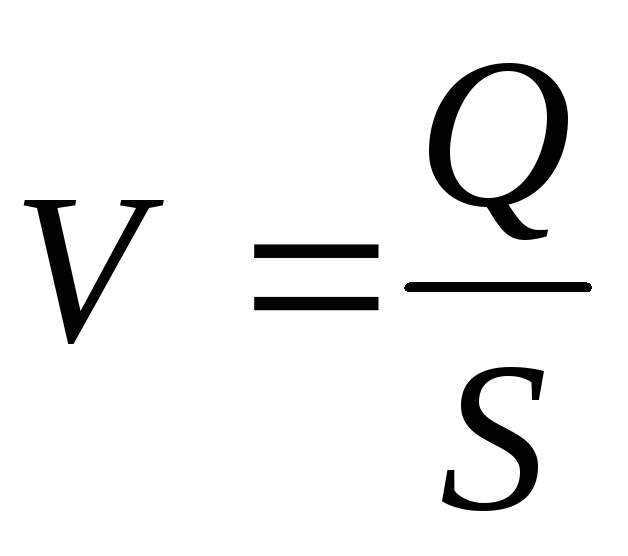 ,
, 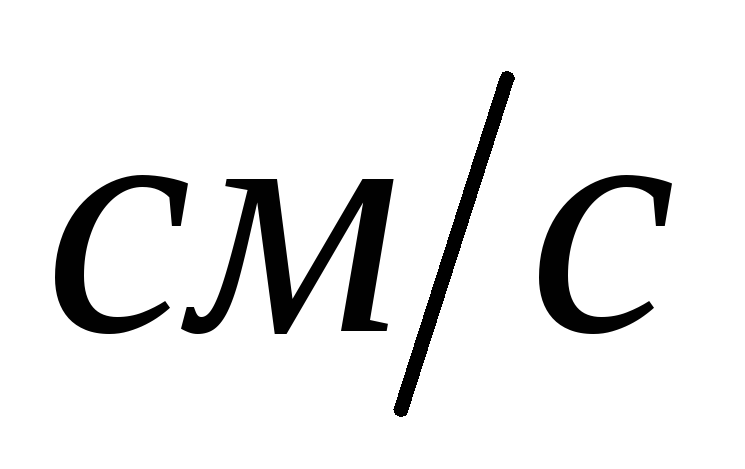 .
(10)
.
(10)
4. Из приложения определяют кинематический коэффициент вязкости воды n см2 /с в соответствии с измеренной температурой °С.
5. Вычисляют число Рейнольдса Re, соответствующее каждому опыту и устанавливают зону гидравлического сопротивления:
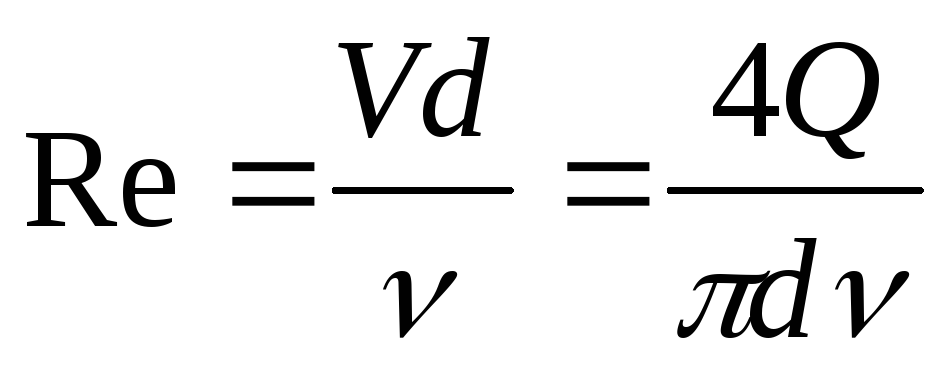 (11)
(11)
6. Вычисляют опытное значение коэффициента гидравлического трения по формуле
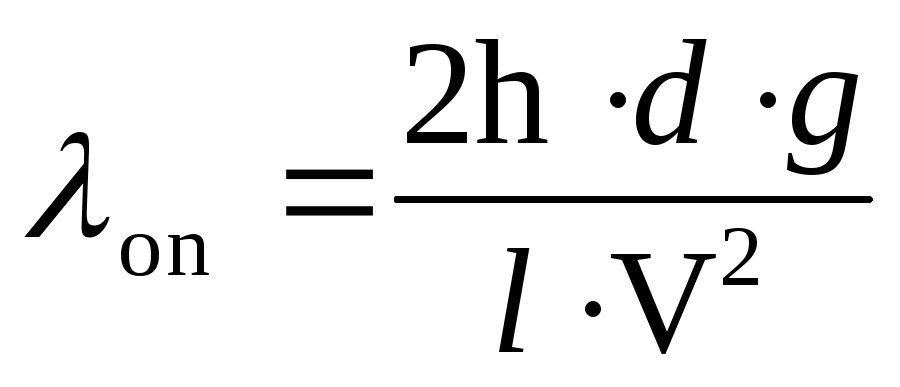 .
(12)
.
(12)
7 Вычисляют теоретическое значение коэффициента гидравлического трения по формуле, соответствующей зоне сопротивления .
8. Определяют расхождение коэффициентов гидравлического трения
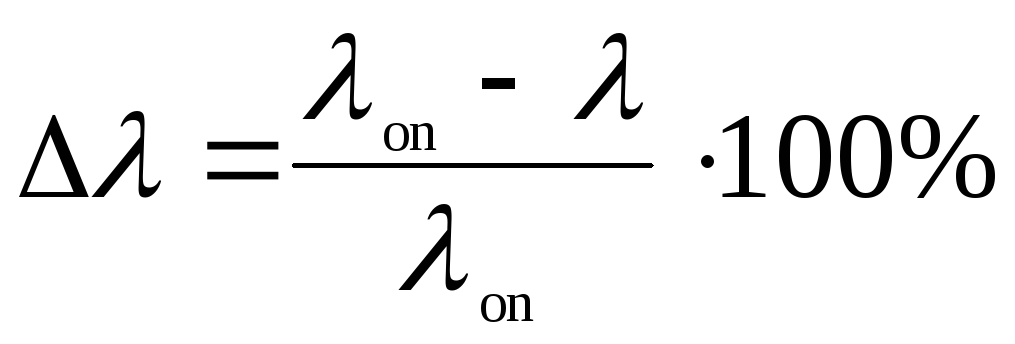 .
.
9. Делают выводы о соответствии теоретического и опытного коэффициентах гидравлического трения и характере изменения коэффициента в зависимости от числа Рейнольдса.
Определение погрешности эксперимента
Случайными погрешностями пренебрегают и рассматривают только систематические погрешности. Погрешность определения площади, расхода, скорости и коэффициента гидравлического трения находится как погрешность косвенных измерений.
Согласно выражениям (8) — (12), относительная погрешность определения площади, расхода, скорости и коэффициента гидравлического трения составит:
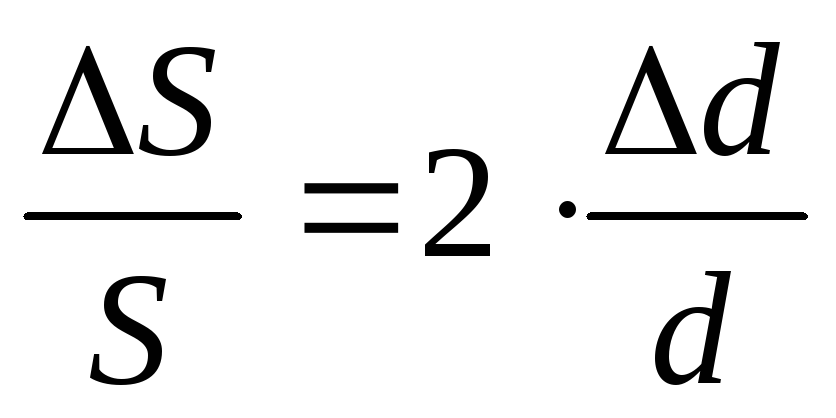 ,
(13)
,
(13)
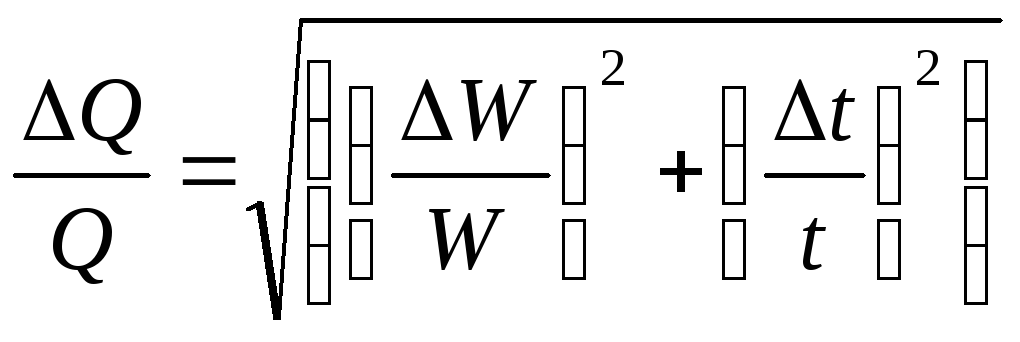 ,
(14)
,
(14)
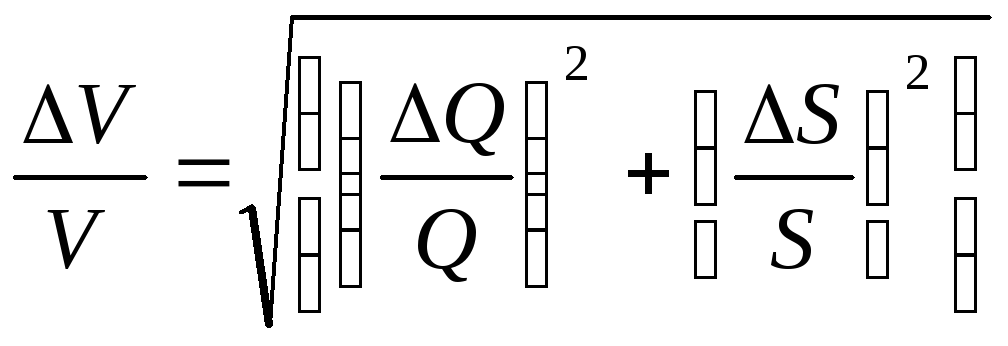 ,
(15)
,
(15)
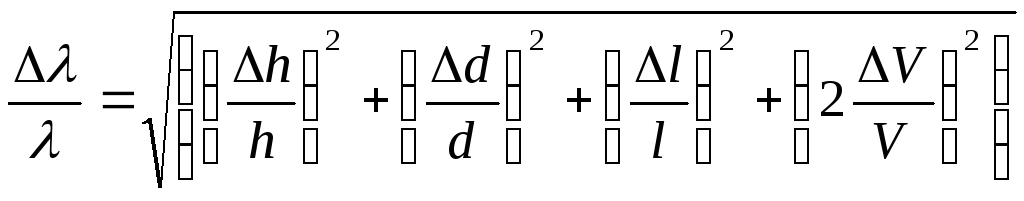 ,
(16)
,
(16)
Через  обозначены абсолютные ошибки измерения
отдельных величин, входящих в выражения.
обозначены абсолютные ошибки измерения
отдельных величин, входящих в выражения.
В данной работе экспериментально измеряется время наполнения мерной емкости, уровень воды в пьезометрах и её температура.
Объем мерного сосуда определяют с погрешностью DW = ± 10 см3, время его наполнения с погрешностью Dt = ± 0,2 с, Погрешность кинематического коэффициента вязкости воды n определить в соответствии с погрешностью измерения температуры. Температуру воды определяют при помощи термометра с погрешностью ± 0,5 °С. Внутренний диаметр трубы измеряется по дубликату при помощи штангенциркуля с погрешностью не более 0,1 мм.
Погрешности по формулам (13 — 16) рассчитываются для каждого сопротивления и всех опытов. Далее делается анализ полученных результатов, намечаются пути увеличения точности опытов. По согласованию с преподавателем каждым студентом звена делается расчет одного из предложенных мероприятий по снижению погрешности. По результатам всех расчетов делается общий вывод о возможности увеличении точности опытов до заданной преподавателем величины.
СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА ПО РАБОТЕ
Отчет по работе каждым студентом оформляется письменно в отдельной тетради и должен содержать :
1. Название лабораторной работы.
2. Формулировку цели работы.
3. Некоторые основные понятия и формулы.
4. Схему и описание лабораторной установки.
5. Таблицу с результатами опыта.
6. Выводы.
При рукописном оформлении схема установки, таблицы выполняются в карандаше с использованием чертежных приборов. Желательно выполнение отчета полностью на компьютере.
Гидравлические потери. Коэффициент сопротивления. Коэффициент сопротивления трения.
Гидравлические потери при движении жидкости по трубопроводу зависят от формы и размеров его поперечного сечения, шероховатости стенок, скорости течения и вязкости жидкости.
Экспериментально установлено, что гидравлические потери пропорциональны квадрату скорости, поэтому принят следующий способ выражения гидравлических потерь полного напора в единицах длины:
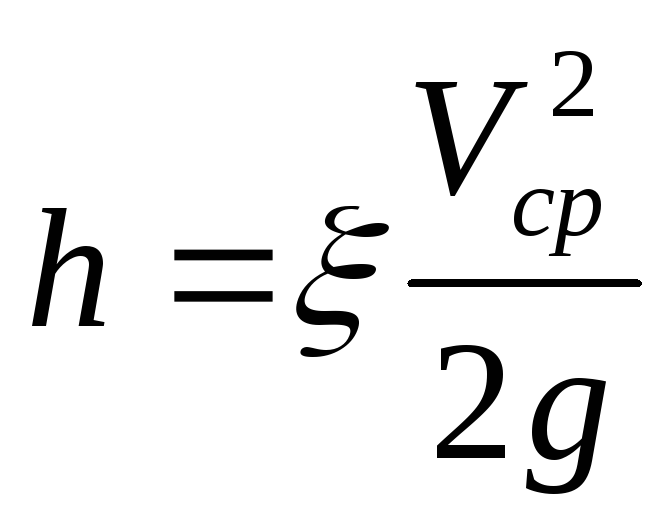
где – коэффициент сопротивления.
Выделяют два типа гидравлических потерь – местные и потери на трение. Местные потери обусловлены изменением величины и величины и направления вектора скорости на участке трубопровода, длина которого соизмерима с диаметром.
В качестве примеров местных сопротивлений могут служить вентили, задвижки, колена, диафрагмы, и т.п. Местные потери определяются по формуле
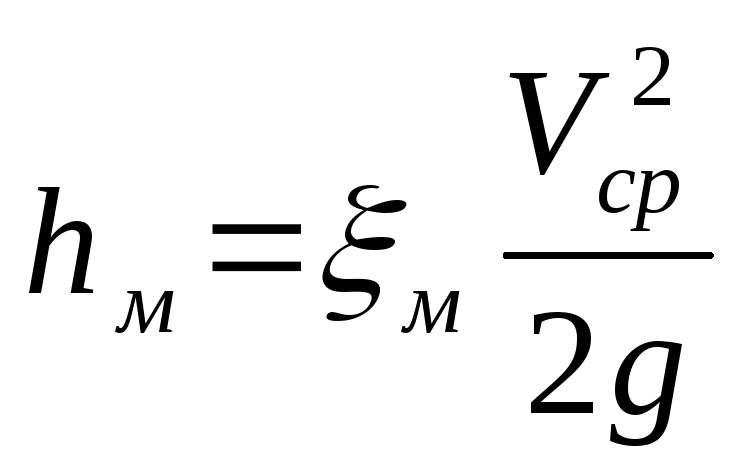
которая носит название формулы Вейсбаха. Здесь Vcp – средняя скорость, соответствующая меньшему из сечений подводящего или отводящего трубопровода, м – коэффициент местного сопротивления.
Потери по длине или потери на трение возникают в прямолинейных трубопроводах постоянного сечения. Они обусловлены вязкостью жидкости и поэтому существуют в трубах с любой сколь угодно малой шероховатостью стенок. Эти потери линейно связаны с длиной трубы, поэтому для их определения используется формула Дарси
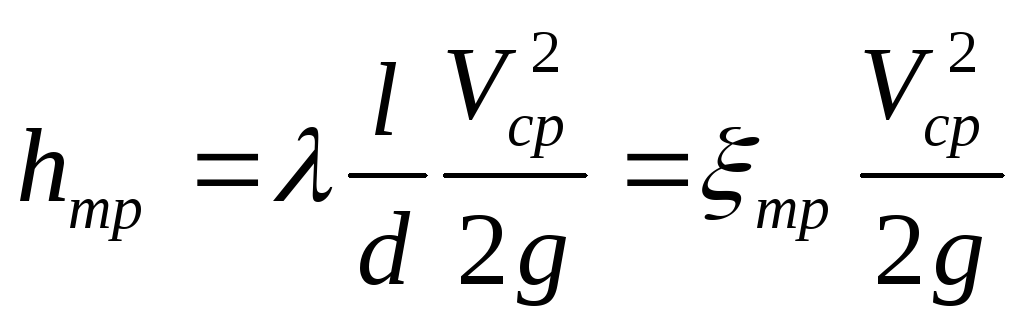
где λ– коэффициент потерь на трение (сопротивление трения участка трубы, длина которого равна диаметру).
Определение гидравлических потерь в трубопроводах является одним из основных вопросов гидравлики.
Гидродинамические измерения и приборы
Измерения параметров потока производится с помощью измерительной цепи, состоящей из одного или нескольких датчиков, соединительных элементов и измерительных приборов. Основными измеряемыми параметрами являются перепады давления и расходы (скорости движения) жидкости,
Необходимо различать абсолютное и относительное давления. Абсолютным называется разность давлений между измеряемой величиной и абсолютным вакуумом. Оно измеряется барометрами. Относительным (избыточным) называется разность между измеряемым давлением и давлением, принятым за базовое, в качестве которого часто используют атмосферное. Относительное давление измеряется манометрами.
Абсолютное давление всегда положительно. Относительное давление может быть и отрицательным, если измеряемое давление меньше базового. Такие перепады измеряются вакуумметрами.
Простейшим манометром является стеклянная трубка, верхний конец которой открыт атмосферу, а нижний подключен к приемнику давления. Такое устройство называется жидкостным манометром или пьезометром, поскольку им измеряется пьезометрический напор р/, представляющий собой высоту подъема жидкости под действием давления р (рис. 3, а). Величина давления вычисляется по формуле
p=h
где h– высота подъема жидкости в пьезометре.
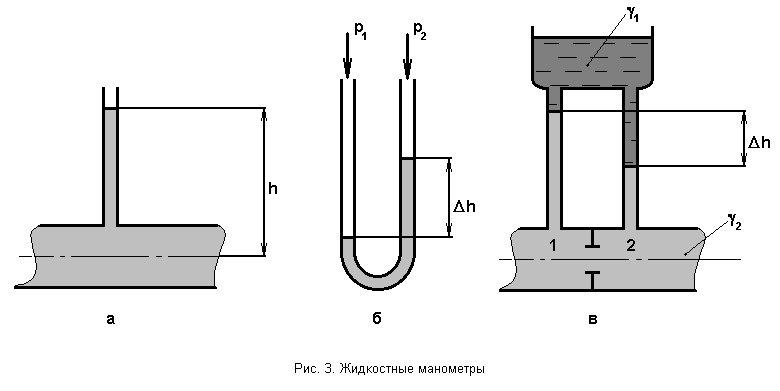
Рабочей жидкостью в пьезометре обычно является вода. Этим ограничивается их область применения, т. к. максимальные замеряемые перепады не превышают 1,5-2,0м, что соответствует давлениям 0,15-0,2 атм. (0.15-0,2 МПа).
Кроме пьезометров широкое распространение получили U-образные дифференциальные жидкостные манометры (рис. 3,б), в которые заливается жидкость, имеющая большую плотность, чем та, давление в которой измеряется. Дифференциальными эти манометры называются потому, что ими измеряется разность явлений, подаваемых на оба конца U-образной трубки.
Большие перепады давлений (200-1000 атм.) замеряются механическими манометрами. Очень малые перепады давления измеряются двужидкостными дифференциальными манометрами (рис. 3, в), для которых
Δp=(1—2)Δh
Манометры являются измерительными приборами. Устройства, через которые производится отбор сигнала (давления), называются датчиками или приемниками. Они бывают 2-х типов: приемники статического и полного напора.
Приемником статического давления является отверстие в стенке прямолинейного участка трубопровода постоянного поперечного сечения. Отверстие должно быть выполнено по нормали к стенке трубопровода (рис. 4, а). Оно не должно вносить искажений в поток жидкости, поэтому его выполняют диаметром 1-2 мм. Дальнейшее увеличение диаметра нецелесообразно в связи с увеличением инерционности системы замера.
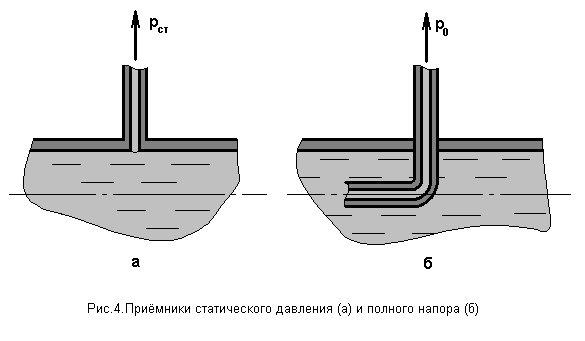
Полный напор измеряется с помощью трубки, установленной параллельно вектору скорости и открытой навстречу потоку (рис. 4, б).
Покажем, что давление, измеряемое с помощью этого датчика, равно полному напору. Для этого запишем уравнение Бернулли (12) для двух сечений линии тока, одно из которых расположено в невозмущенном потоке (индекс 1), а второе у входа в приемник (индекс 0). При z1=z0 получим
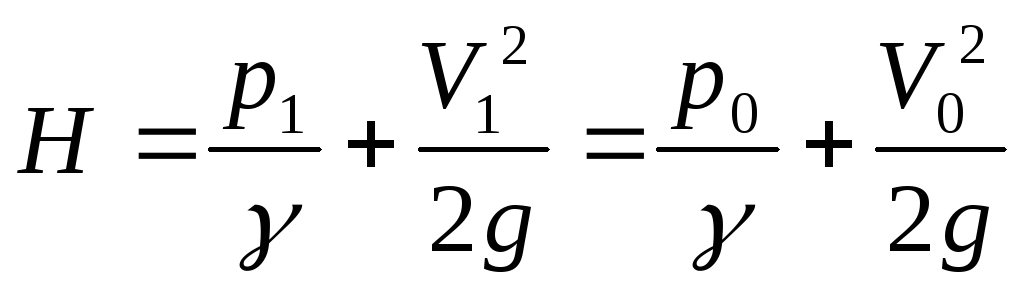
У входа в приемник давления скорость потока равна нулю (V0=0), тогда пьезометрический напор, замеряемый этим приемником, будет равен полному напору, т.е.
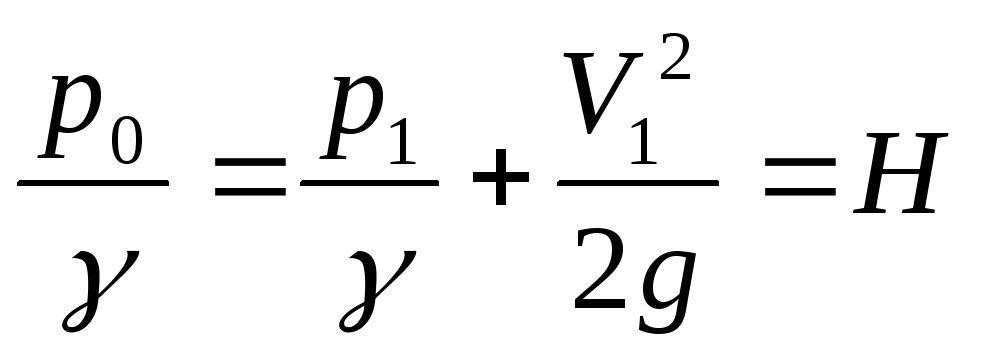
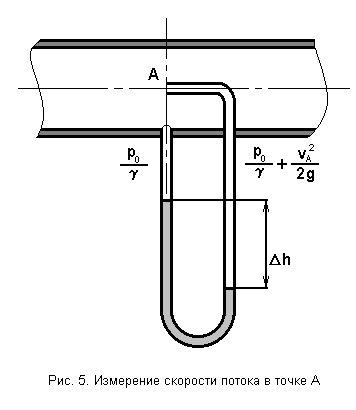
Отсюда следует, что если в некотором сечении трубопровода расположить приемники полного и статического давлений и подключить их к дифференциальному манометру (рис 5), то из уравнения (19) с учетом формулы (20) можно определить скорость потока в точке А сечения
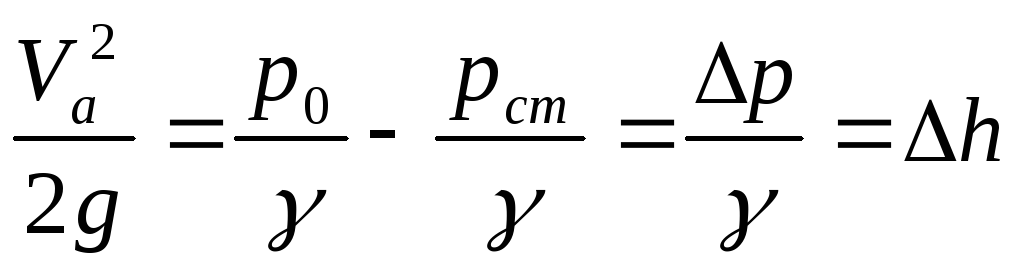
или
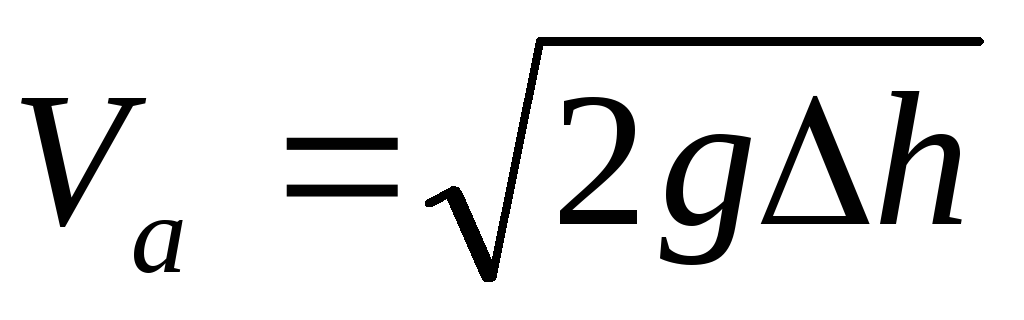 .
.
Формула Дарси — Вейсбаха — Википедия
Формула Вейсбаха’[1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом в 1855 году):
- Δh=ξ⋅V22g,{\displaystyle \Delta h=\xi \cdot {\frac {V^{2}}{2g}},}
где
Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
- ΔP=ξ⋅V22⋅ρ,{\displaystyle \Delta P=\xi \cdot {\frac {V^{2}}{2}}\cdot \rho ,}
где
- ΔP{\displaystyle \Delta P} — потери давления на гидравлическом сопротивлении;
- ρ{\displaystyle \rho } — плотность жидкости.
Если гидравлическое сопротивление представляет собой участок трубы длиной L{\displaystyle L} и диаметром D{\displaystyle D}, то коэффициент Дарси определяется следующим образом:
- ξ=λ⋅LD,{\displaystyle \xi =\lambda \cdot {\frac {L}{D}},}
где λ{\displaystyle \lambda } — коэффициент потерь на трение по длине.
Тогда формула Вейсбаха приобретает вид:
- Δh=λ⋅LD⋅V22g,{\displaystyle \Delta h=\lambda \cdot {\frac {L}{D}}\cdot {\frac {V^{2}}{2g}},}
или для потери давления:
- ΔP=λ⋅LD⋅V22⋅ρ.{\displaystyle \Delta P=\lambda \cdot {\frac {L}{D}}\cdot {\frac {V^{2}}{2}}\cdot \rho .}
Последние две зависимости получили название формулы Дарси — Вейсбаха[2]. Предложена Ю. Вейсбахом (L. J. Weisbach, 1845) и А. Дарси (1857).
Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то D{\displaystyle D} представляет собой гидравлический диаметр.
Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.
Определение коэффициента потерь на трение по длине[править | править код]
Коэффициент λ{\displaystyle \lambda } определяется по-разному для разных случаев.
Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле Пуазейля:
- λ=64Re,{\displaystyle \lambda ={\frac {64}{\mathrm {Re} }},}
где Re{\displaystyle \mathrm {Re} } — число Рейнольдса.
Иногда для гибких труб в расчётах принимают
- λ=68Re.{\displaystyle \lambda ={\frac {68}{\mathrm {Re} }}.}
Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:
- λ=0,316Re4.{\displaystyle \lambda ={\frac {0,316}{\sqrt[{4}]{\mathrm {Re} }}}.}
Эта формула даёт хорошие результаты при числах Рейнольдса, изменяющихся в пределах от критического числа Рейнольдса Reкр{\displaystyle \mathrm {Re_{\text{кр}}} } до значений Re=105{\displaystyle \mathrm {Re} =10^{5}}. Формула Блазиуса применяется для гидравлически гладких труб.
Для значений Re=105−106{\displaystyle \mathrm {Re} =10^{5}-10^{6}} применяют формулу Никурадзе: λ=0,0032+0,221/Re0,237.{\textstyle \lambda =0,0032+0,221/Re^{0,237}.}[3] Также, применяются формулы Женеро, Альтшуля, Канакова и других.
Для значений Рейнольдса больше 104{\displaystyle 10^{4}} применяется формула Горшкова-Кантакузена, полученная методом регрессионного анализа[4]: λ=0,2579Re0,231.{\displaystyle \lambda ={\frac {0,2579}{\mathrm {Re^{0,231}} }}.} Тем же автором была выведена формула для вычисления критерия Рейнольдса в гемодинамике (течении крови).[5]
Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).
Определение коэффициента Дарси для местных сопротивлений[править | править код]
Рис. 1. Гидравлический конфузор: Q1{\displaystyle Q_{1}} — поток жидкости в широком сечении трубы; Q2{\displaystyle Q_{2}} — поток жидкости в узком сечении трубыДля каждого вида местных сопротивлений существуют свои зависимости для определения коэффициента ξ{\displaystyle \xi }.
К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.
1. При внезапном расширении трубы:
- ξ=(1−S1S2)2,{\displaystyle \xi =\left(1-{\frac {S_{1}}{S_{2}}}\right)^{2},}
где S1{\displaystyle S_{1}} и S2{\displaystyle S_{2}} — площади поперечного сечения трубы, соответственно перед расширением и после него.
2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:
Рис. 2. Зависимость коэффициента Дарси от угла δ{\displaystyle \delta } поворота трубы- ξ=1−S2/S12,{\displaystyle \xi ={\frac {1-S_{2}/S_{1}}{2}},}
где S1{\displaystyle S_{1}} и S2{\displaystyle S_{2}} — площади поперечного сечения трубы, соответственно, перед сужением и после него.
3. При постепенном сужении трубы (конфузор):
- ξ=λT8sinα/2(1−1n2),{\displaystyle \xi ={\frac {\lambda _{T}}{8\sin {\alpha /2}}}\left(1-{\frac {1}{n^{2}}}\right),}
где n=S1S2{\displaystyle n={\frac {S_{1}}{S_{2}}}} — степень сужения; λT{\displaystyle \lambda _{T}} — коэффициент потерь на трение по длине при турбулентном режиме.
4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).
Исторически формула Дарси — Вейсбаха была получена как вариант формулы Прони.
- ↑ Формула Вейсбаха в Физической энциклопедии
- ↑ Дарси-Вейсбаха формула в Физической энциклопедии
- ↑ М.П. Малков, И.Б. Данилов, А.Г. Зельдович, А.Б. Фрадков. Справочник по физико-техническим основам криогеники. — «Энергия», 1973. — С. 242-243. — 392 с.
- ↑ Горшков-Кантакузен В. А. К вопросу вычисления коэффициента Дарси методом регрессионного анализа // Материалы XXI Международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред» имени А. Г. Горшкова, 16 – 20 февраля 2015, Вятичи.. — 2015. — № Том 1. — С. 59-60. — ISSN 978-5-906099-81-5.
- ↑ Горшков-Кантакузен В.А. Вычисление критерия Рейнольдса в рамках гемодинамики // Бюллетень НЦССХ им. А.Н. Бакулева «сердечно-сосудистые заболевания» : (Приложение). — май-июнь 2015. — № 3 Т.6. — С. С. 180. — ISSN 1810-0694.
- Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др. — 2-е изд., перераб. — М.: Машиностроение, 1982.
- Гейер В. Г., Дулин В. С., Заря А. Н. Гидравлика и гидропривод: Учеб для вузов. — 3-е изд., перераб. и доп. — М.: Недра, 1991.
- Горшков-Кантакузен В. А. К вопросу вычисления коэффициента Дарси методом регрессионного анализа // Материалы XXI Международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред» имени А. Г. Горшкова, 16 — 20 февраля 2015, Вятичи. Том 1 / МАИ. — М.: ООО «ТРП», 2015. С. 59-60
Коэффициент гидравлического сопротивления трения труб
Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения.
Калькулятор расчета коэффициента гидравлического сопротивления трения труб
| Расход жидкости | |
| Коэффициент кинематической вязкости ( для воды тем-рой 100C = 1,3, 200C = 1) | |
| Диаметр трубопровода | |
| Длина трубопровода | |
| Плотность жидкости | |
| Коэффициент шероховатости стенок трубопровода | |
| Выберите тип трубопроводаЦельнотянутые (Латунь-Медь-Сталь)Цельнотянутые (Стальные новые)Цельнотянутые стальные(Б\У)Цельносварные стальныеКлепаные стальныеИз кровельной сталиОценкованые стальныеЧугунные новыеЧугунные водопроводыеЖелезобетонные новыеАсбстоцементныеСтеклянныеЖелезобетонные | |
| Режим течения | |
| Скорость движения жидкости в трубопроводе, м/c | |
| Число Рейнольдса (Re) | |
| Коэффициент трения (λ) | |
| Коэффициент гидравлического сопротивления (ξ) | |
| Потеря давления (Δp), Па | |
0
0
Было ли это полезно?Гидравлические потери принято разделять на два вида:
- потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;
- местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости через элемент гидравлической системы пропорциональны квадрату скорости жидкости. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ, которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что

То есть в предположении, что скорость w по всему сечению потока одинакова, ζ=Δp/eторм, где eторм = ρw²/2 —энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w=Q/F, где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость[1]. Таким образом, средняя энергия торможения потока обычно несколько больше ρw²/2, см. Среднее квадратическое.
Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) λ, фигурирующего в формуле Дарси — Вейсбаха
где L — длина элемента, d — характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления
таким образом, для линейного элемента относительной длины L/d коэффициент сопротивления трения ζтр=λL/d.
Связанные Калькуляторы
Гидравлические потери по длине
Потери напора по
длине, иначе их называют потерями напора
на трение 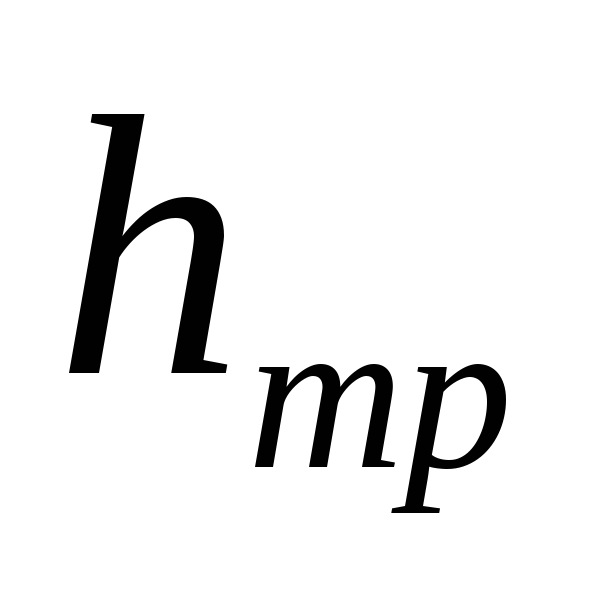 ,
в чистом виде, т.е. так, что нет никаких
других потерь, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловлены внутренним трением в
жидкости и поэтому происходят и в
шероховатых трубах, и в гладких. Величина
этих потерь выражается зависимостью
,
в чистом виде, т.е. так, что нет никаких
других потерь, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловлены внутренним трением в
жидкости и поэтому происходят и в
шероховатых трубах, и в гладких. Величина
этих потерь выражается зависимостью
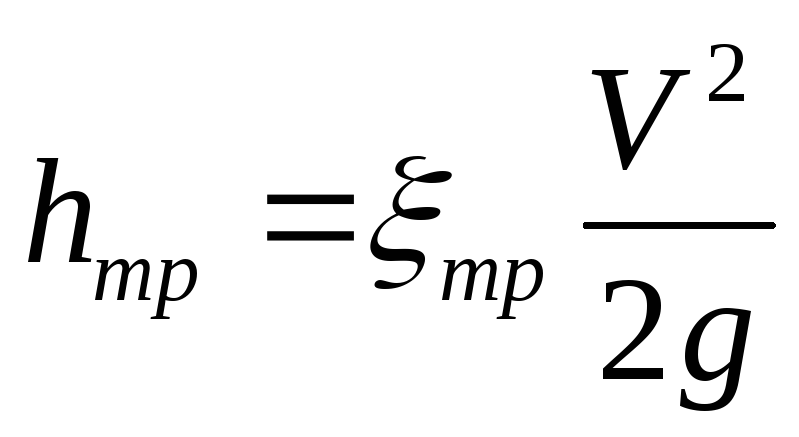 ,
,
где 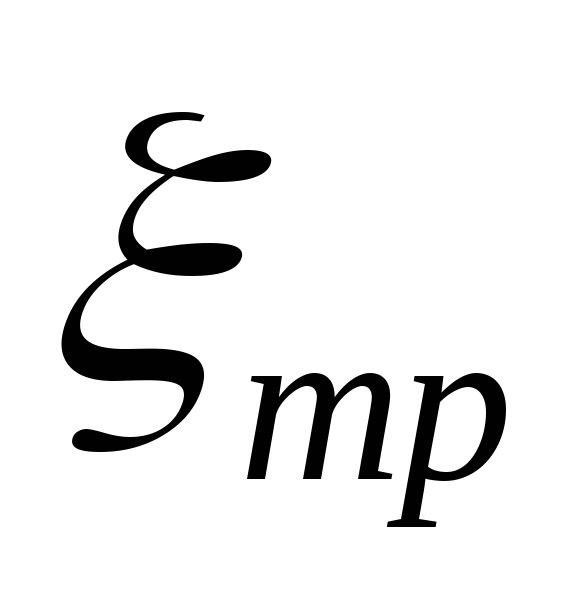 — коэффициент сопротивления, обусловленный
трением по длине.
— коэффициент сопротивления, обусловленный
трением по длине.
При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы
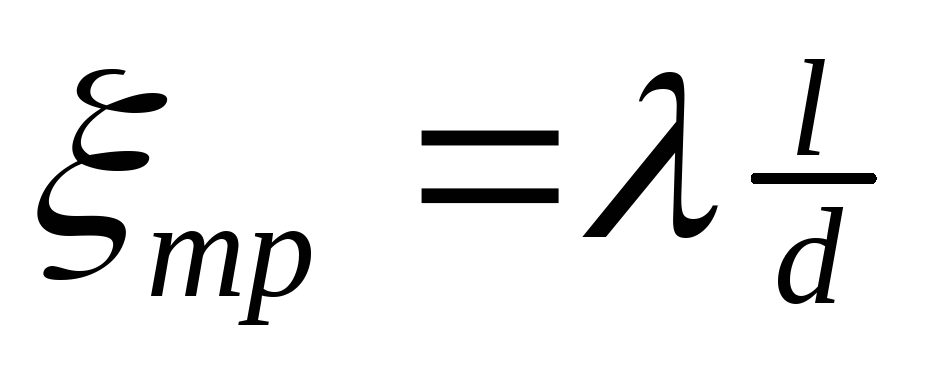 ,
,
где – коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).
Из этого выражения нетрудно видеть, что значение — коэффициент трения участка круглой трубы, длина которого равна её диаметру.
С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси
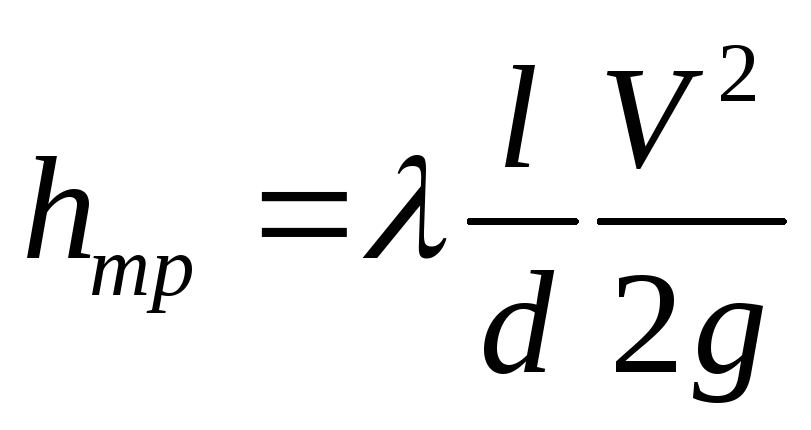 .
.
Эту формулу можно
применять не только для цилиндрических
трубопроводов, но тогда надо выразить
диаметр трубопровода d через гидравлический
радиус потока 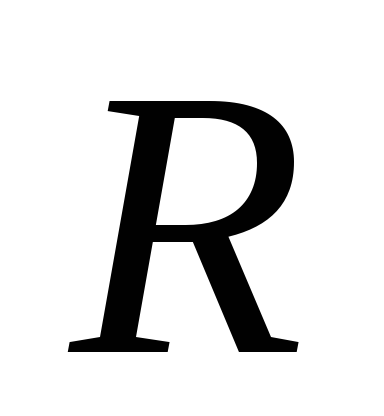
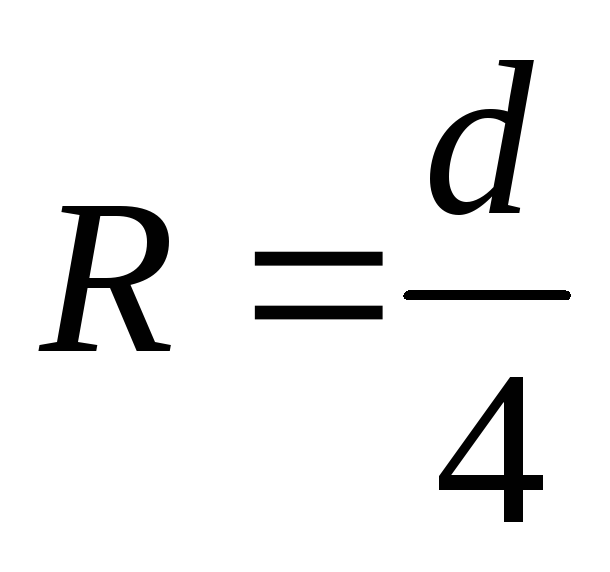 или
или 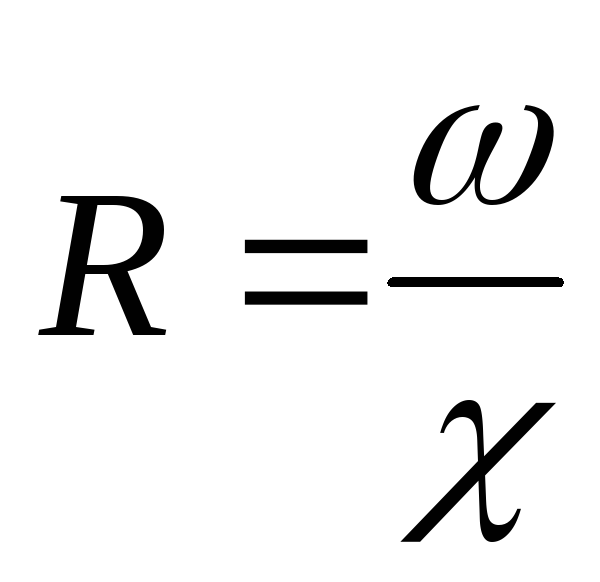
где, напомним, ω – площадь живого сечения потока,
χ — смоченный периметр.
Гидравлический радиус можно вычислить для потока с любой формой сечения, и тогда формула Дарси принимает вид
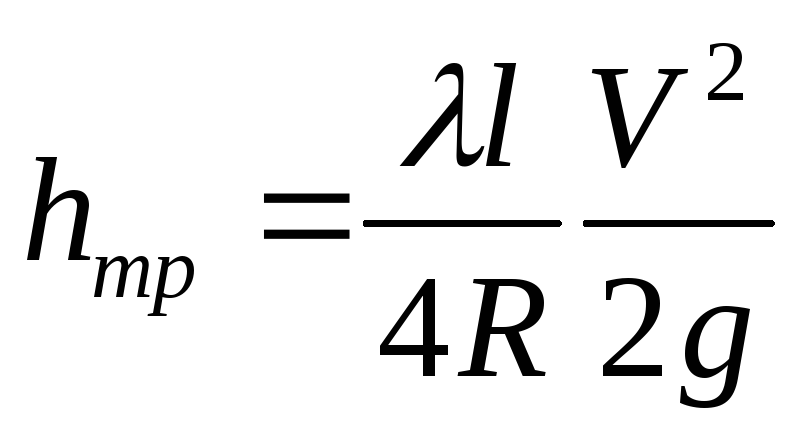 .
.
Эта формула справедлива как для ламинарного, так и для турбулентного режимов движения жидкости, однако коэффициент трения по длине λ не является величиной постоянной.
Д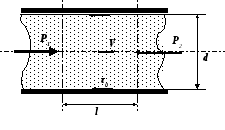 ля
определения физического смысла
коэффициентаλ рассмотрим объём жидкости длиной l,
который равномерно движется в трубе
диаметром d со скоростью V.
На этот объём действуют силы давления P1и P2,
причём P1 > P2,
и силы трения рассматриваемого объёма
о стенки трубы, которые определяются
напряжением трения на стенке трубы τ0.
Условием равномерного движения под
действием сказанных сил будет следующее
равенство:
ля
определения физического смысла
коэффициентаλ рассмотрим объём жидкости длиной l,
который равномерно движется в трубе
диаметром d со скоростью V.
На этот объём действуют силы давления P1и P2,
причём P1 > P2,
и силы трения рассматриваемого объёма
о стенки трубы, которые определяются
напряжением трения на стенке трубы τ0.
Условием равномерного движения под
действием сказанных сил будет следующее
равенство:
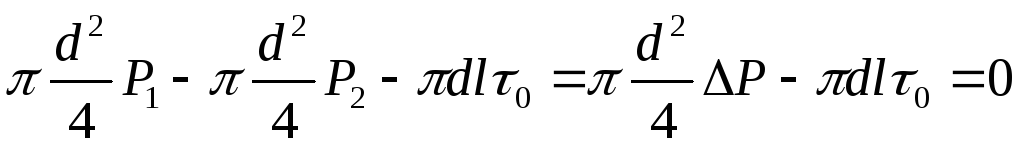 .
.
Если учесть, что
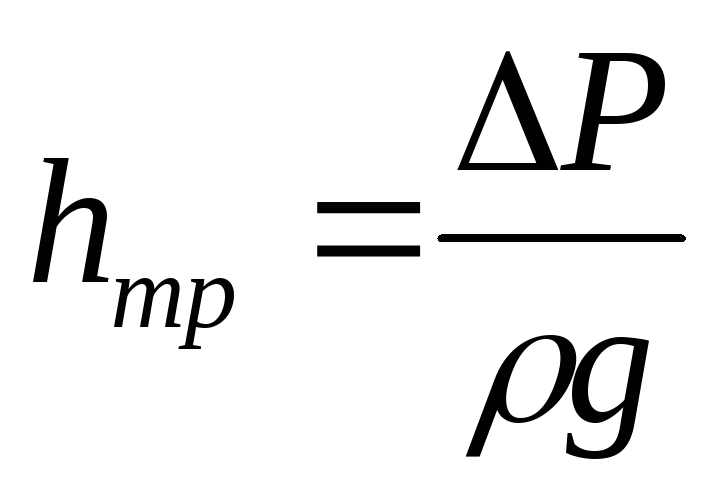 , то
, то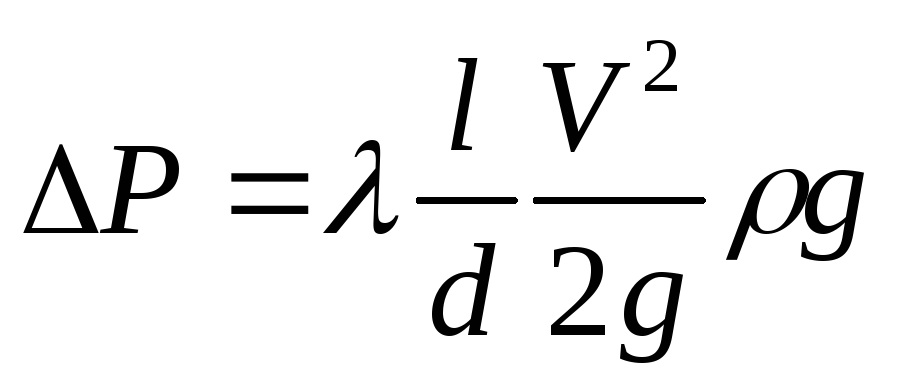 ,
,
и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим:
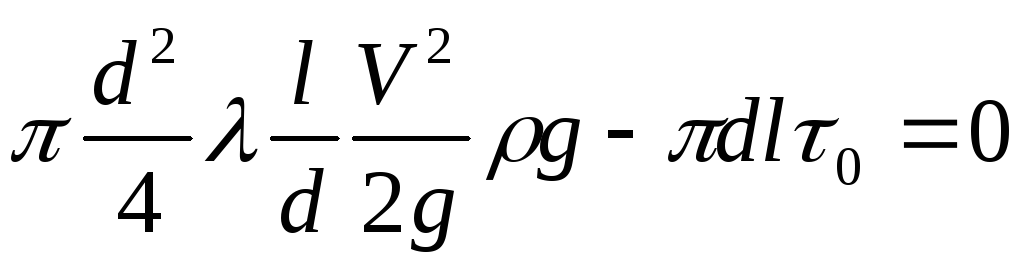 .
.
Сократив последнее
выражение, получим 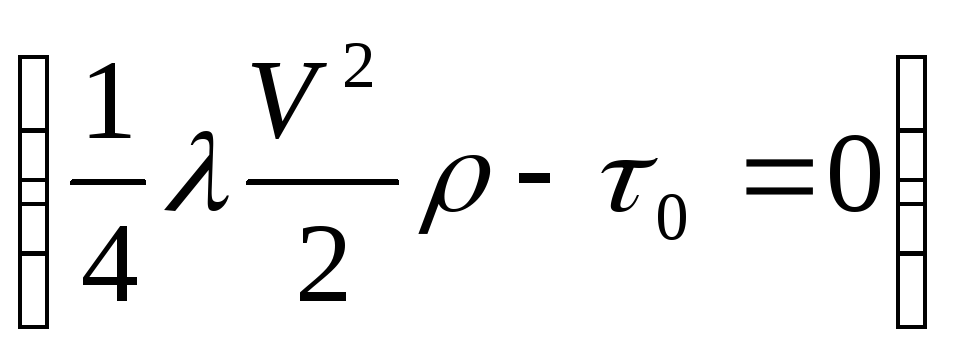 . Выразив из негоλ,
окончательно будем иметь
. Выразив из негоλ,
окончательно будем иметь
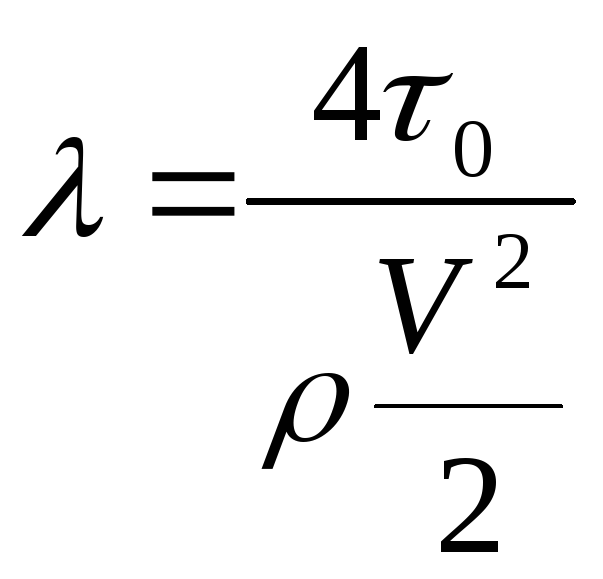 .
.
Из полученного выражения следует, что коэффициент гидравлического трения есть величина, пропорциональная отношению напряжения трения на стенке трубы к гидродинамическому давлению, посчитанному по средней скорости потока. Приведённые выше рассуждения и полученные в результате них формулы справедливы как для ламинарного, так и для турбулентного потоков. Однако коэффициент λ не является величиной постоянной и зависит от многих факторов. Для выяснения его величины, и связанных с ним потерь энергии необходимо подробно проанализировать режимы движения жидкости.
Ламинарное течение жидкости
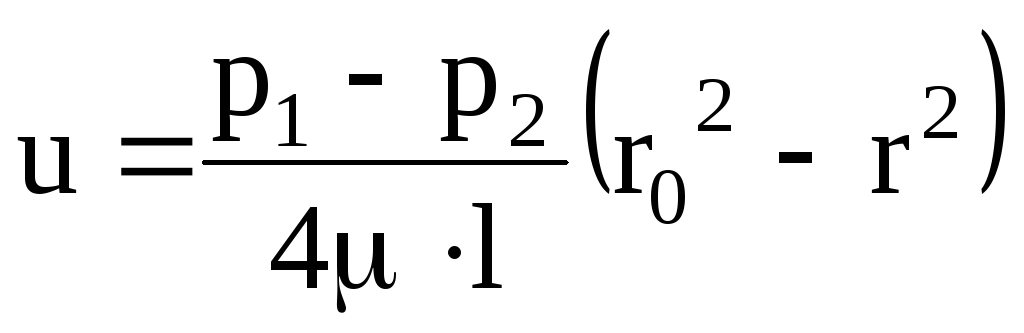
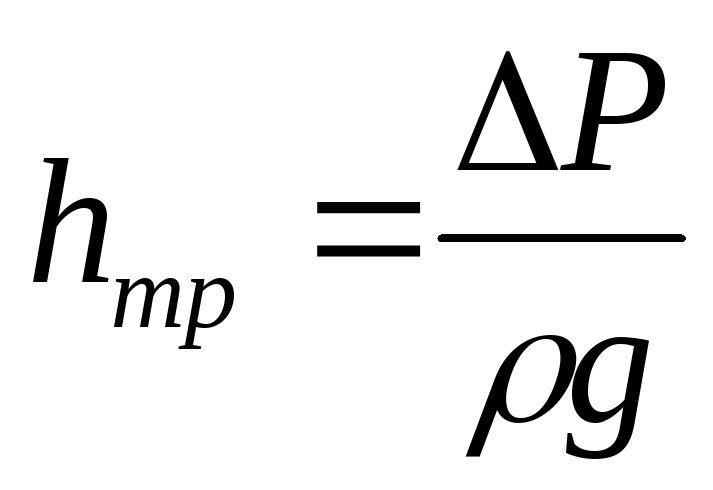

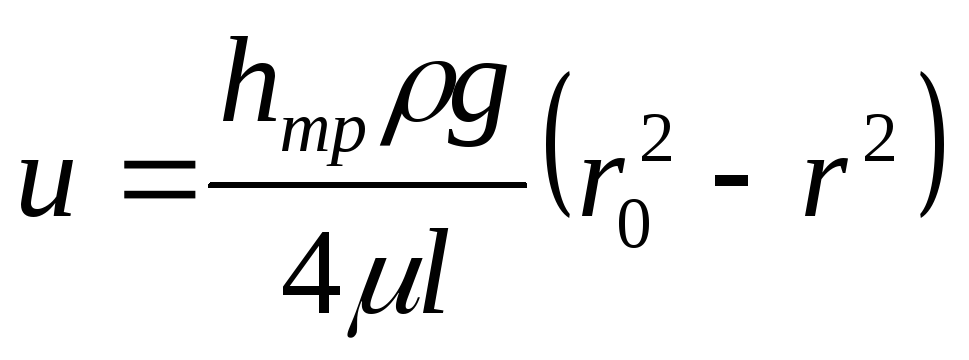
Используя значение скорости u, определим величину расхода через кольцевую площадь dωc шириной dr, находящуюся на расстоянии r от центра трубы. Выше было отмечено, что скорость в любой точке этого кольца одинакова, и тогда

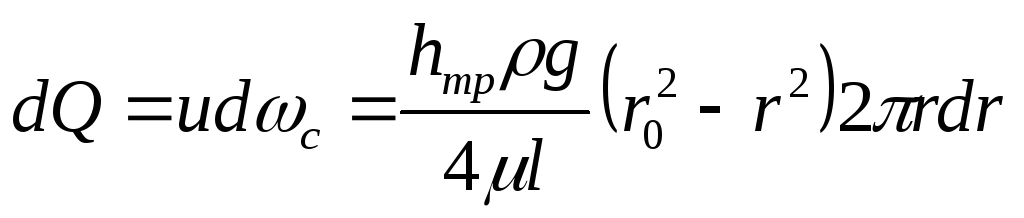 .
.
Проинтегрировав dQ по всей площади трубы (т.е. от r = 0 до r = r0), получим
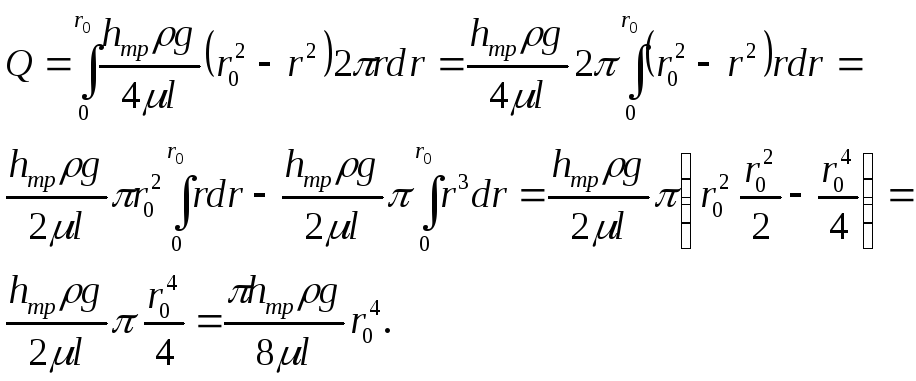
Средняя скорость в таком потоке будет
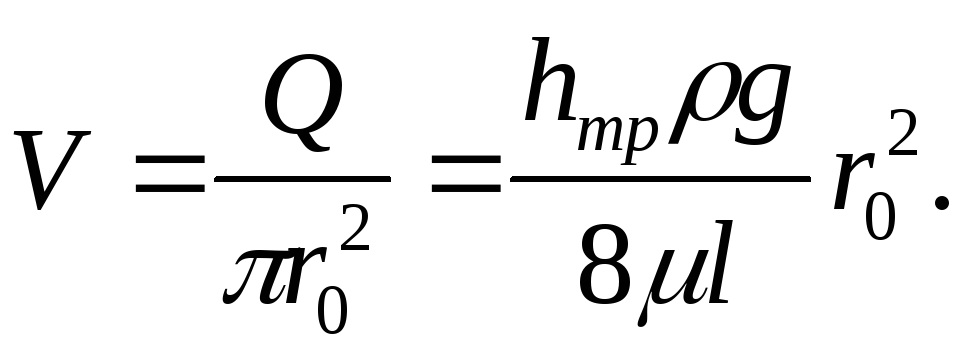
Заметим, что средняя скорость потока с параболическим распределением скоростей вдвое меньше максимальной.
Из последнего выражения легко получить закон сопротивления потоку, т.е. зависимость потерь энергии от размеров и параметров движения жидкости:
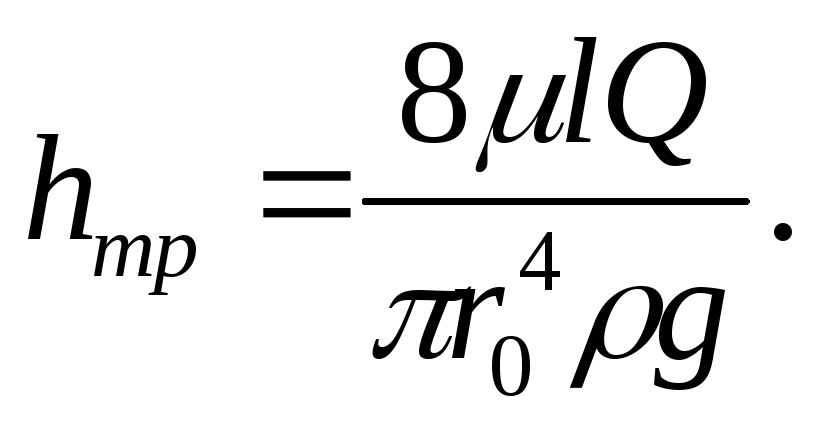
Заменив в этом
выражении динамический коэффициент
вязкости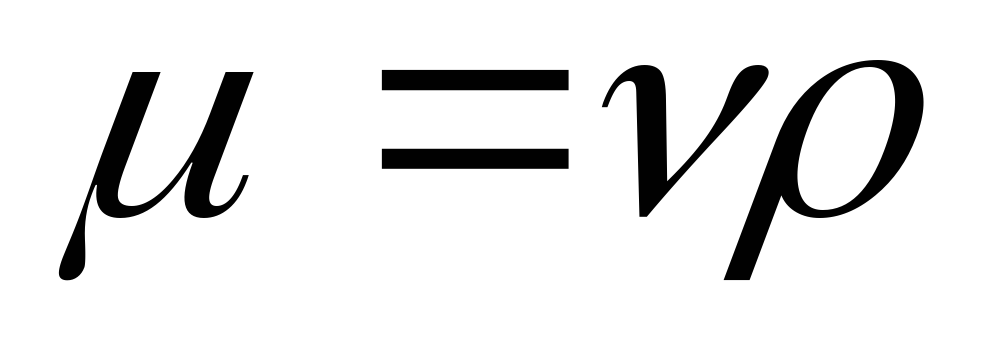 кинематическим и выразив радиус трубыr0 через диаметр d, получим
кинематическим и выразив радиус трубыr0 через диаметр d, получим
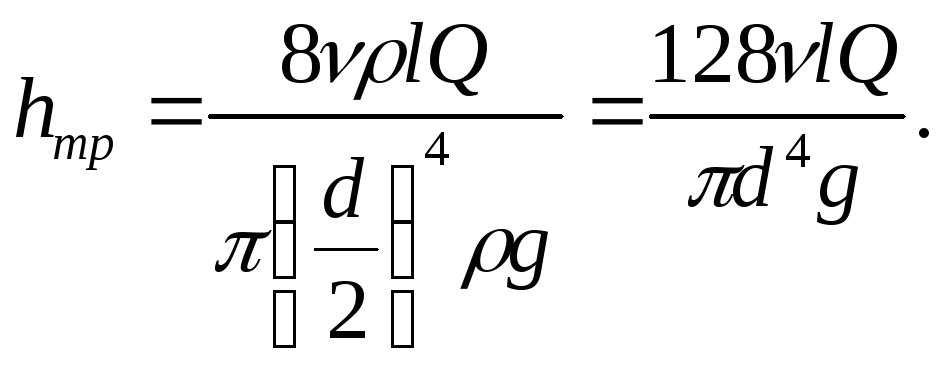
Полученное выражение носит название закона Пуазейля и применяется для расчета потерь энергии с ламинарным течением.
Эту же величину потерь на трение ранее мы выразили формулой Дарси. Если приравнять правые части формулы Дарси и закона Пуазейля, получится:
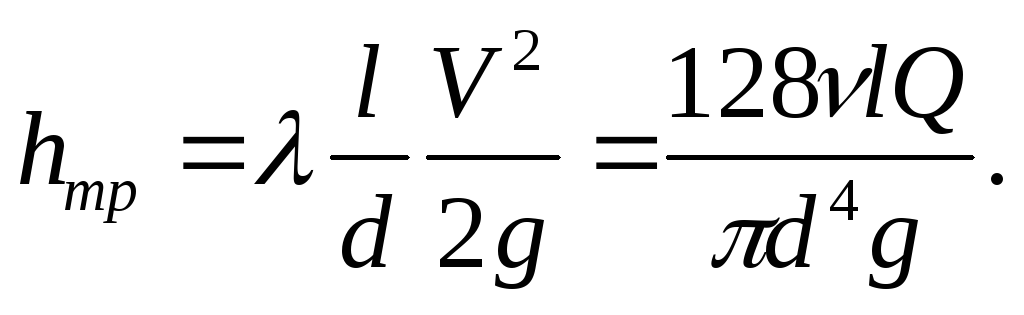
Заменим расход
произведением 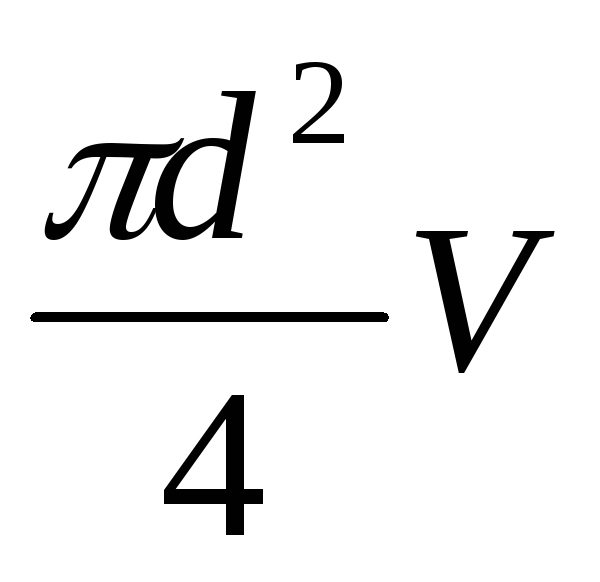 и подставим в последнее равенство
и подставим в последнее равенство
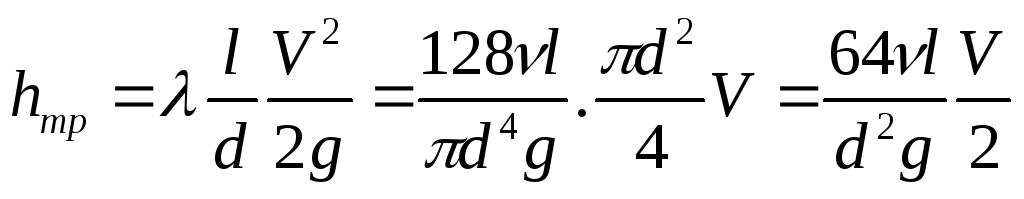 .
.
Искусственно умножим и разделим числитель и знаменатель на V:
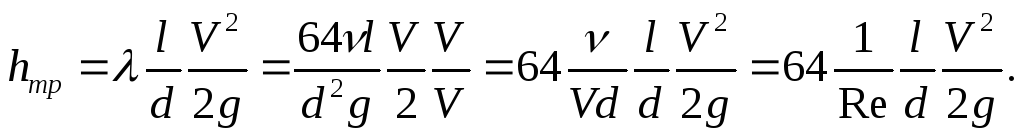
Очевидно, что в этом случае
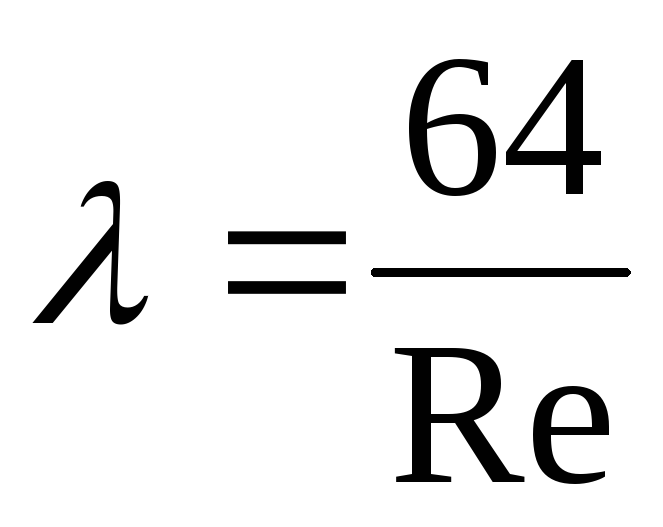 .
.
Это выражение для
коэффициента гидравлического трения
при ламинарном движении жидкости хорошо
подтверждается экспериментом и
используется на практике для определения
потерь энергии в потоке при ламинарном
течении. Иногда этот коэффициент
обозначается 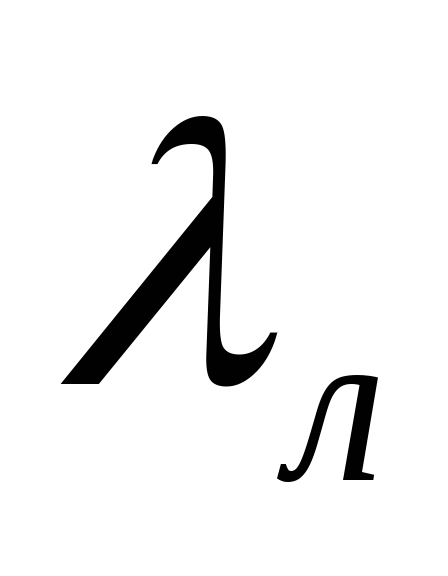 .
.
11. Потери напора по длине. Порядок определения коэффициента трения.
Потери
напора по длине иначе называют потерями
напора на трение, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловленны внутренним трением в
жидкости и поэтому происходит и в
шероховатых трубах, и в гладких. Основной
расчетной формулой для потерь напора
при ламинарном и турбулентном режиме
движения в круглых трубах является формула
Вейсбаха-Дарси 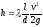
V-средняя скорость движения
Коэффициент
трения зависит от числа Рейнольдса и
от безразмерного геометрического
фактора- относительной шероховатости 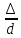 (
( —
абсолютное значение эквивалентной
шероховатости )
—
абсолютное значение эквивалентной
шероховатости )
Коэффициент
трения при ламинарном режиме движения
жидкости 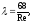
Область турбулентного и переходного режимов разбиваются на 3 области :
1)
область гидравлически гладких труб 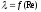
2)
область доквадратического сопротивления
шероховатых труб 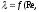
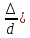
3)
область квадратичного сопротивления
шероховатых труб 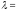 f
f 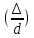
При
турбулентном режиме движения жидкости
коэффициент движения определяется по
графику Мурина и по формуле Альтшуля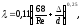
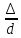 относительная
шероховатость трубопровода
относительная
шероховатость трубопровода
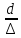 относительная
гладкость трубопровода
относительная
гладкость трубопровода
Величину абсолютной эквивалентной шероховатости при расчетах берут из справочника в зависимости от материала труб и состояния его внутренней поверхности.
12.Местные гидравлические сопротивления. Потери напора на местных сопротивлениях.
Местные сопротивления это такие участки трубопровода, на которых происходит деформация потока, т.е. происходит изменения скорости потока или по величине или по направлению.
К местным сопротивлениям относятся: вход и выход потока из трубы, внезапные сужения и расширения труб, плавные сужения и расширения труб колена, отводы, тройники, диафрагмы, регулирующие устройства (краны, вентили, задвижки и т.д)
Протекая через местное сопротивление, поток деформируется, возникают пульсации скоростей и давлений, образуются вихревые зоны с обратными токами вследствие отрыва потока от стенок трубопровода. На эти процессы смешения и вихреобразования тратится часть полной энергии потока, которая превращается в тепло и рассеивается в окружающее пространство.
Различают четыре вида местных сопротивлений
Местные сопротивления на которых происходит изменение скорости по величине (рис.25 на стр.52)
Местные сопротивления связанные с изменением направления движения жидкости (рис. 26 на стр.52)
Местные сопротивления на которых происходит смешение или разделение потока(рис.27 на стр. 53)
Трубопроводная арматура(краны, вентили, задвижки, расходомеры и т.п.)
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
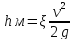
где -коэффициент
местного сопротивления,
-коэффициент
местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
13.Виды потерь напора(давлений) в трубопроводах. Расчетные формулы.
Потери напора по длине потока. Иначе их называют потерями напора на трение, возникают в гладких прямых трубах с постоянным сечение при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят в шероховатых трубах, и в гладких.
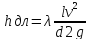
где -коэффициент гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
коэффициент
трения 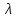 зависит от числа РейнольдсаRe(режима
движения жидкости) и от безразмерного
геометрического фактора-относительной
шероховатости
зависит от числа РейнольдсаRe(режима
движения жидкости) и от безразмерного
геометрического фактора-относительной
шероховатости 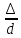 (или
(или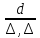 -абсолютное
значение эквивалентной шероховатости)
-абсолютное
значение эквивалентной шероховатости)
коэффициент трения при ламинарном режиме движения жидкости рассчитывается по формуле:
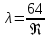
На практике при турбулентном режиме движения коэффициент трения может быть определен по графику Г.А.Мурина или рассчитан по формуле А.Д.Альтшуля:
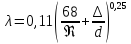
Где Re-критерий Рейнольдса;
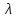 -коэффициент
трения;
-коэффициент
трения;
 -абсолютное
значение эквивалентной шероховатости,
м;
-абсолютное
значение эквивалентной шероховатости,
м;
d- диаметр трубопровода, м;
Потери напорана местное сопротивления.
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
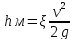
где -коэффициент
местного сопротивления,
-коэффициент
местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
Принцип сложения потерь напора.
Как правило, трубопроводы имеют прямые участки и множество местных сопротивлений. Принцип сложения потерь напора заключается в том, что потери напора по длине и потери напора на местных сопротивлениях складываются, т.е общие потери напора:
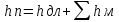
т.е 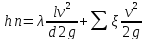
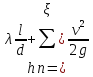
где где 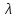 -коэффициент
гидравлического трения,
-коэффициент
гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
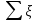 -сумма
коэффициентов местных сопротивлений.
-сумма
коэффициентов местных сопротивлений.
Часто
в расчетах требуется определить потерю
давления 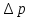 .
.
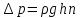
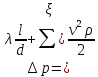
Потеря давления в трубопроводе на трение(для участка прямого трубопровода, длинного трубопровода), вычисляется по формуле
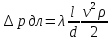
«Определение коэффициентов гидравлического трения трубопровода и коэффициентов местных потерь напора».
Выполнил: студент группы 04-СУ-2 КСФ Калинин П. А.
Ответы на контрольные вопросы к лабораторной работе №1.
«Определение основных характеристик потока».
Вопрос: Дайте определение вязкости жидкости.
О.: Вязкость – это свойство жидкости сопротивляться деформации сдвига, т. е. относительному смещению ее слоев.
В: Назовите характеристики вязкости, их размерность и связь между ними.
О: Характеристиками
вязкости являются динамический
и кинематический
коэффициенты, которые связаны между
собой соотношением: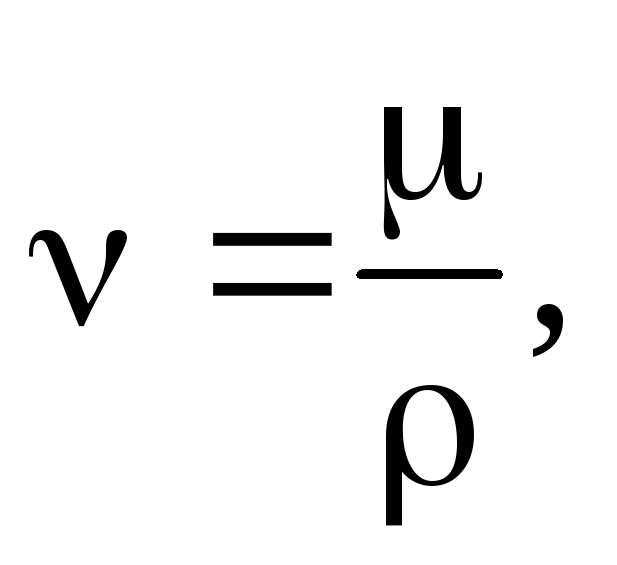 где ρ – плотность жидкости. Единицей
динамического коэффициента вязкости
является Па·с, а кинематического
коэффициента – м2/с.
где ρ – плотность жидкости. Единицей
динамического коэффициента вязкости
является Па·с, а кинематического
коэффициента – м2/с.
В: Как изменяется вязкость капельных жидкостей и газов при изменении температуры и давления.
О: При повышении температуры вязкость капельной жидкости уменьшается, а вязкость газов увеличивается. Вязкость жидкости зависит также от давления, но эта зависимость заметно проявляется при больших изменениях давления.
В: Что называется расходом жидкости и каковы единицы его измерения?
О: Расходом называется количество жидкости, протекающее через незамкнутую поверхность в единицу времени. Если это количество измеряется в единицах объема, то расход называется объемным и измеряется в м3/с или в л/с.
В: Дайте определение средней скорости потока.
О: Средняя скорость потока – это такая условная, постоянная для всех точек сечения скорость vср , при которой расход жидкости через это сечение будет таким же, как и при действительном распределении скоростей частиц жидкости в данном сечении.
В: Какое различие между установившимся и неустановившимся движением жидкости?
О: Установившимся называют такое движение, при котором скорости частиц жидкости в любой точке пространства не изменяются во времени. При неустановившемся движении скорости частиц в точках пространства изменяются во времени.
В: В чем состоит отличие ламинарного режима от турбулентного?
О: При ламинарном режиме частицы жидкости движутся упорядоченно, образуя слоистое течение. При турбулентном режиме частицы, наряду с основным движением по некоторому преимущественному направлению, перемещаются из слоя в слой (происходит перемешивание частиц), их мгновенные скорости резко изменяются по величине и направлению.
В: Перечислите факторы, от которых зависит режим течения жидкости.
О: На режим движения жидкости оказывают влияние следующие факторы: вязкость жидкости , плотность ρ, характерный линейный размер потока l и средняя скорость vср .
В: В чем смысл числа Рейнольдса?
О: Число Рейнольдса является критерием, определяющим режим движения жидкости.
В: Какова связь между полным, статическим и динамическим давлением?
О: Динамическое давление есть разность полного и статического давлений.
B: Как связано динамическое давление со скоростью напора?
О: Динамическое
давление пропорционально квадрату
скорости напора. 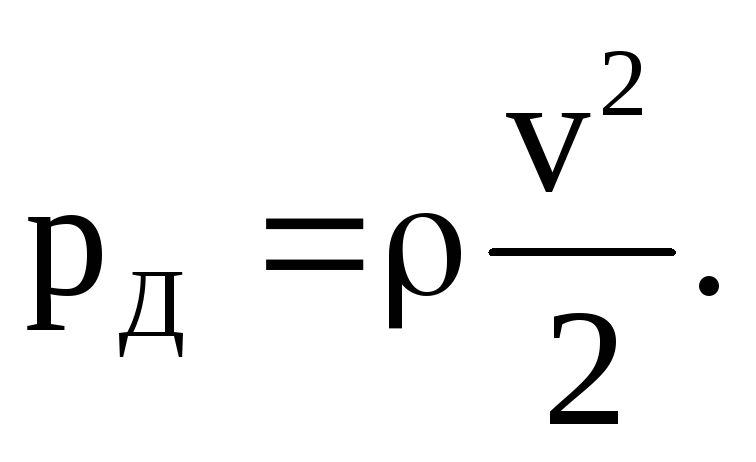
В: Каковы причины неравномерного распределения скорости в поперечном сечении потока реальной жидкости?
О: Вблизи стенок канала, вследствие вязкости, жидкость движется медленнее, чем на удалении. На самой стенке скорость равна нулю, т. е. частицы прилипают. Закон распределения скоростей зависит от режима движения жидкости.
В: Что представляет собой коэффициент кинетической энергии (коэф-нт Кориолиса)?
О: Коэффициент кинетической энергии представляет собой отношение кинетической энергии в сечении потока при истинных скоростях v к кинетической энергии в том же сечении, вычисленной по средней скорости vср.
Ответы на контрольные вопросы к лабораторной работе №2.
«Экспериментальная иллюстрация уравнения Бернулли».
Вопрос: Перечислите формы механической энергии движущейся жидкости.
Ответ: Механическая энергия движущейся жидкости может иметь три формы:
потенциальную энергию положения
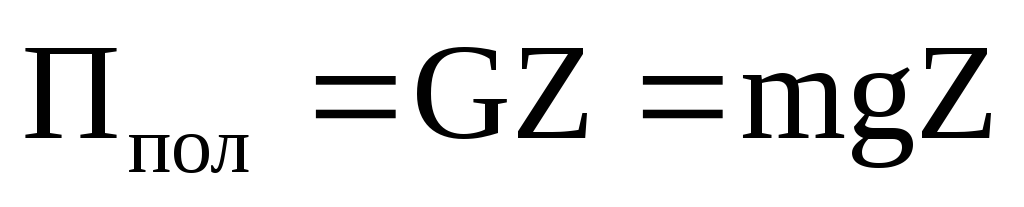 ;
;потенциальную энергию давления
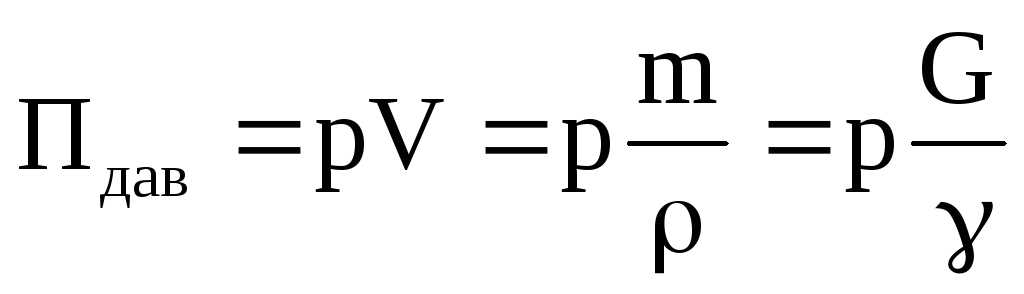 ;
;кинетическую энергию
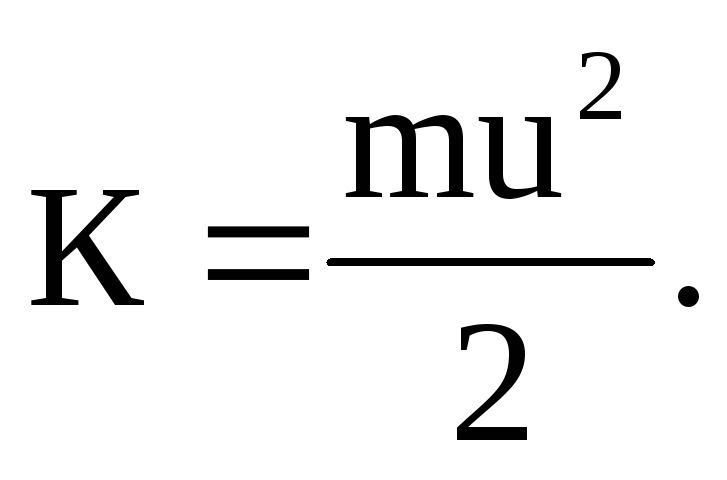
В: Дайте определение удельной энергии жидкости и напора.
О: Удельная энергия (напор) – это энергия, отнесенная к единице веса жидкости.
В: В чем отличие в записи уравнения Бернулли для элементарной струйки идеальной и реальной жидкости.
О: При описании потока реальной жидкости скорости берутся средними по сечениям, в связи с чем вводится поправочный коэффициент α.
В: Энергетический и геометрический смысл уравнения Бернулли и входящих в него членов.
О: Запишем уравнение Бернулли в двух видах
1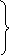 .
.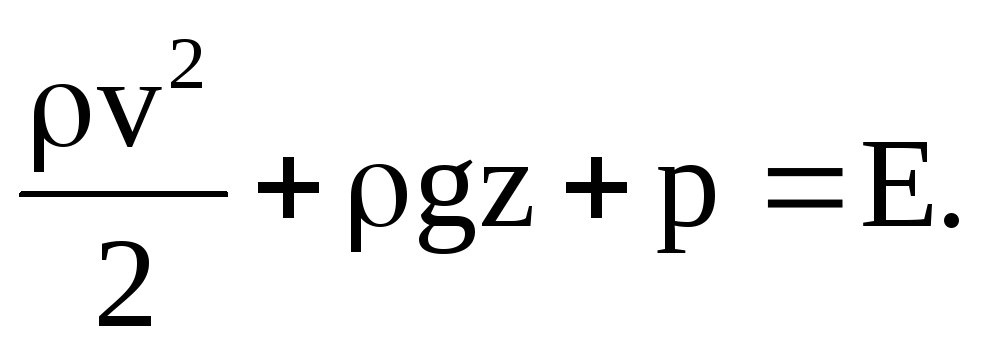
Здесь 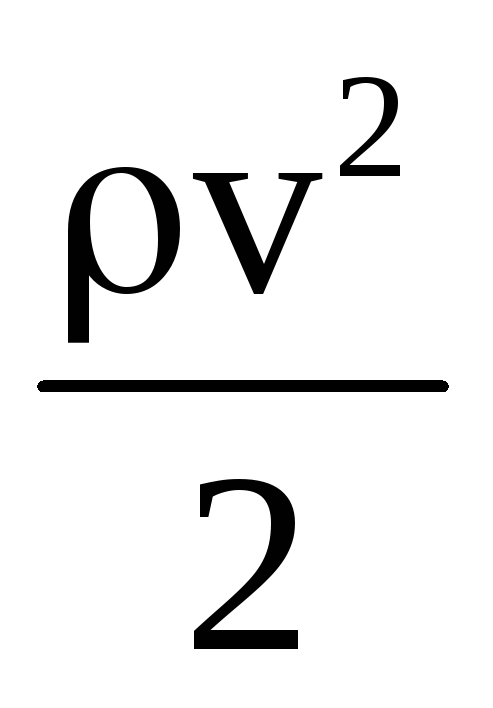 – удельная кинетическая энергия,
– удельная кинетическая энергия,
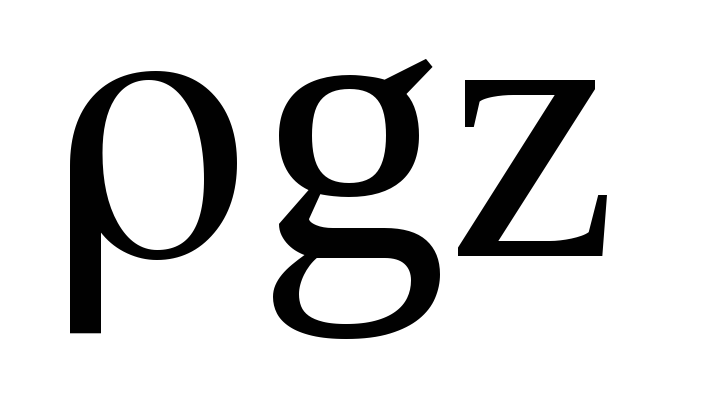 –удельная
потенциальная энергия положения,
энергетический смысл.
–удельная
потенциальная энергия положения,
энергетический смысл.
 –удельная
потенциальная энергия положения.
–удельная
потенциальная энергия положения.
 –полная удельная
энергия потока.
–полная удельная
энергия потока.
2.
З десь
десь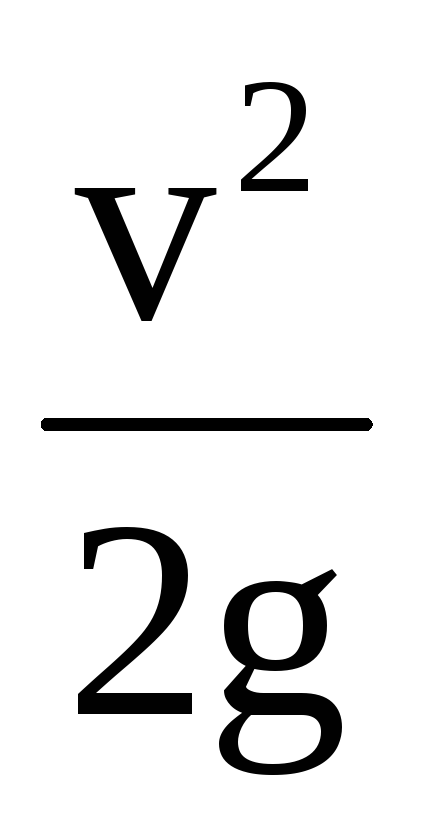 – скоростной напор,
– скоростной напор,
 –геометрический
напор, геометрический смысл.
–геометрический
напор, геометрический смысл.
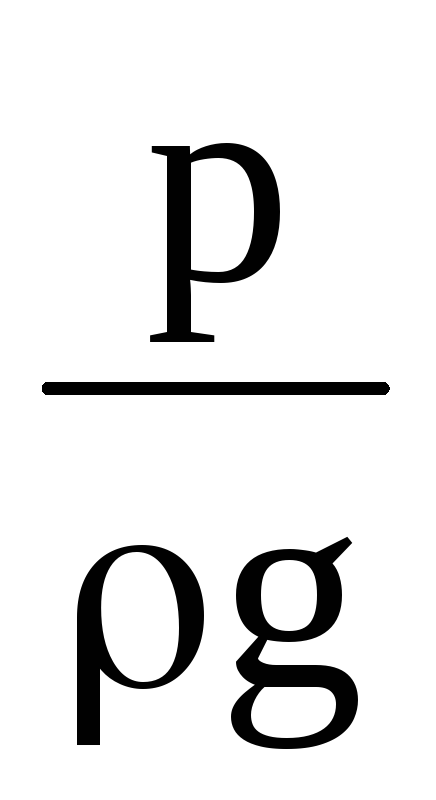 –пьезометрический
напор.
–пьезометрический
напор.
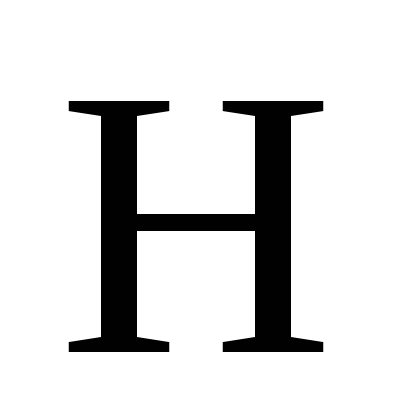 –полный
гидродинамический напор.
–полный
гидродинамический напор.
В: Физический смысл коэффициента кинетической энергии α.
О: Коэффициент
кинетической энергии α
учитывает влияние неравномерности
распределения скоростей по живому
сечению потока на его кинетическую
энергию. 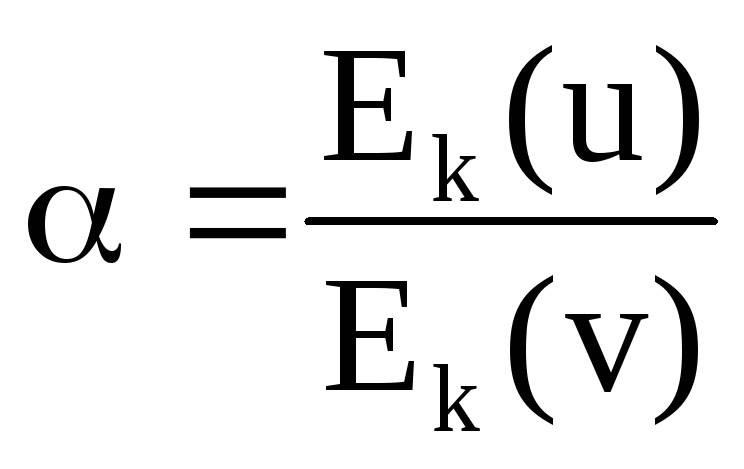
В: Что представляет собой напорная и пьезометрическая линия?
О: Напорная линия – это линия, ординаты которой относительно плоскости сравнения равны полному напору H.
Пьезометрическая
линия – линия, ординаты которой равны
величине потенциального напора 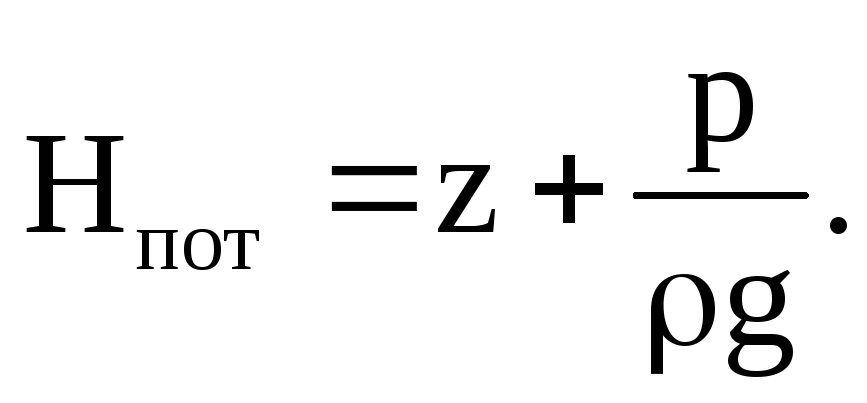
В: Какой характер имеет напорная линия для потока идеальной и реальной жидкости?.
О: Для идеальной жидкости линия полного напора будет параллельна плоскости сравнения. Для реальной жидкости эта линия всегда понижается по течению, поскольку при преодолении гидравлических сопротивлений происходит потеря напора.
В: Как можно измерить полный, пьезометрический, скоростной напор жидкости?
О: Полный напор может быть определен с помощью трубки Пито. Пьезометрический напор измеряется высотой столба жидкости в пьезометре, подключенном к рассматриваемому сечению. Разность показаний трубки Пито и пьезометра, установленных в одном и том же сечении потока, равна местному скоростному напору.
Ответы на контрольные вопросы к лабораторной работе №4.
Вопрос: Что называется потерей напора на преодолении гидравлических сопротивлений?
Ответ: Потерей напора называется уменьшение полной удельной энергии на участке между двумя сечениями потока.
В.: Назовите два вида потерь напора.
О.: Различают два вида гидравлических потерь: потери напора на трение по длине и местные потери напора.
В.: Напишите формулу для определение потерь напора на трение по длине.
О.:
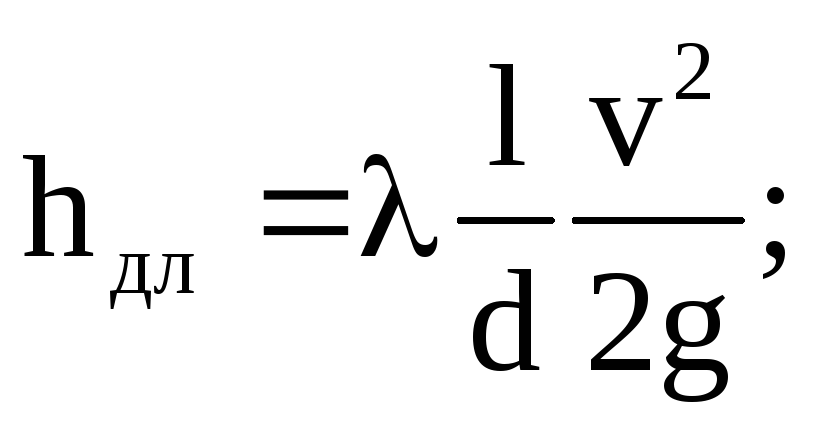
где λ – безразмерный коэффициент гидравлического трения,
l – длина участка трубы, на котором определяются потери напора,
d – внутренний диаметр трубы,
v – средняя скорость потока,
g – ускорение свободного падения.
В.: Отчего зависит коэффициент гидравлического трения λ в общем случае?
О.: Коэффициент λ в общем случае зависит от числа Рейнольдса Re и относительной шероховатости стенок трубы.
В.: Дать определение эквивалентной шероховатости.
О.: Эквивалентная шероховатость это равномерно-зернистая шероховатость, которая по, гидравлическому сопротивлению равноценна естественной абсолютной шероховатости.
В. Какие существуют зоны сопротивления при движении жидкости в трубах? От чего зависит коэффициент λ в каждой зоне?
О.:
Зона 1 вязкостного сопротивления | Зона 2 гидравлически гладких труб | Зона 3 доквадратичного сопротивления | Зона 4 квадратичного сопротивления |
|
|
|
|
В. Какой степени скорости пропорциональна потеря напора по длине для различных зон сопротивления?
О.:
Зона 1 вязкостного сопротивления | Зона 2 гидравлически гладких труб | Зона 3 доквадратичного сопротивления | Зона 4 квадратичного сопротивления |
hдл ~ V | hдл ~ V1,75 | hдл ~ V(1,75÷2,0) | hдл ~ V2 |
В. Чем объясняется возрастание гидравлического сопротивления при переходе от ламинарного режима к турбулентному?
О.: Переход потока в турбулентный режим приводит к сильному возрастанию сопротивления, что связано с увеличением напряжений трения. При этом основная часть сопротивления создается так называемыми турбулентными, касательными напряжениями, возникающими из-за поперечных перемещений (беспорядочного перемешивания) частиц жидкости.
В. От чего зависит степень влияния шероховатости труб на гидравлическое сопротивление при турбулентном режиме?
О.: Степень влияния шероховатости стенок трубы на гидравлическое сопротивление при турбулентном режиме зависит от соотношения толщины ламинарного подслоя 8Л и абсолютной шероховатости Д. По характеру этого влияния различают три зоны турбулентного режима.
В. Почему формула Альтшуля называется универсальной? Для каких зон сопротивления она применима?
О.: Формула Альтшуля является универсальной т.к. она учитывает влияние и шероховатости, и числа Рейнольдса. Она применима для зон турбулентного движения – 2, 3, 4.
В. Напишите формулу для определения местных потерь напора.
О.:
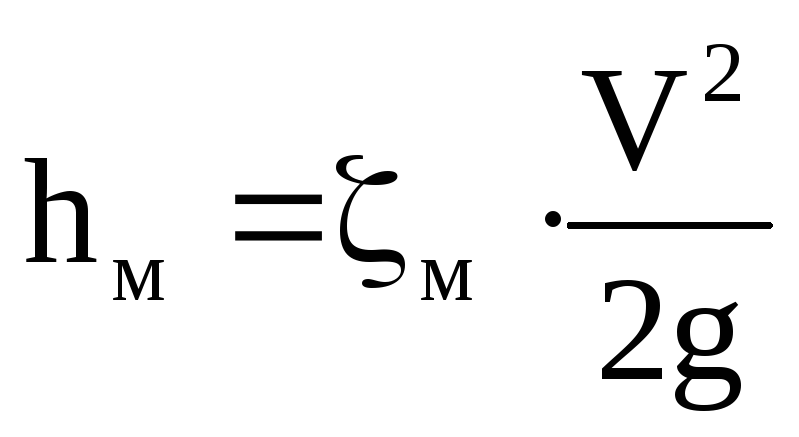
В. От чего зависит коэффициент местного сопротивления ζмпри ламинарном и турбулентном движении?
О.: Величина коэффициента в ζм общем случае зависит от конфигурации местного сопротивления, режима движения жидкости и числа Рейнольдса. В турбулентных потоках при достаточно больших значениях числа Re влияние последнего на коэффициенты ζм незначительно, поэтому в практических расчетах при турбулентном режиме их значения считают зависящими только от вида местного сопротивления и независящими от Re.
В области ламинарного течения коэффициенты ζм зависят и от геометрической формы местного сопротивления, и от числа Re.
В. Дайте определение эквивалентной длины местного сопротивления.
О.: Эквивалентная длина — длина прямого участка трубопровода, на которой потеря напора на трение hдл равна местной потере напора hм, вызываемой данным местным сопротивлением.
В. Как определяются потери напора опытным путем?
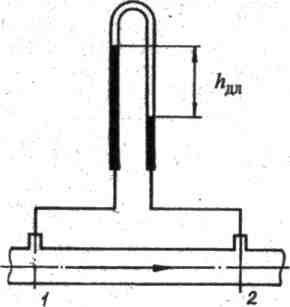
О.: Экспериментально потери напора на трение по длине в трубопроводе постоянного диаметра можно определить непосредственно по показанию дифференциального манометра, подключенного к соответствующим сечениям:
постоянное сечение |
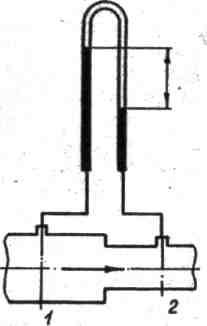
переменное сечение |
Ответы на контрольные вопросы к лабораторной работе №6.